C++结合OpenCV实现RRT算法(路径规划算法)

目录

• 1.RRT算法简介
• 2.算法整体框架流程
• 2.1 rand点的建立
• 2.2 near和new点的建立
• 2.3 安全性检查
• 2.4 算法结束判断
• 3.RRT代码框架
• 3.1 主函数
• 3.2 地图数据的获取
• 3.3 RRT算法的实现
• 3.3.1 起点入树
• 3.3.2 rand点的获取
• 3.3.3 near点的获取
• 3.3.4 new点的获取
• 3.3.5 安全性检测
• 3.4 可视化显示
• 4. 代码运行过程

1.RRT算法简介

代码链接：RRT
动图展示

RRT

2.算法整体框架流程

RRT算法整体框架主要分为rand、near、new三点的建立和near与new之间的安全性检查

2.1 rand点的建立

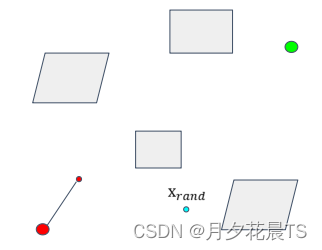
rand点表示在地图 M M M中随机采样获得，记住是随机。我们可以通过设计随机函数，让尽可能的点进入空旷区域，即算法框架中的Sample函数。下图中红色点表示起点，绿色的点表示终点。

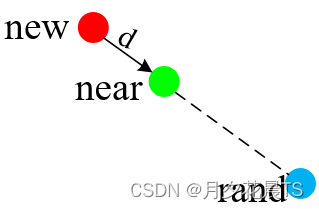
2.2 near和new点的建立

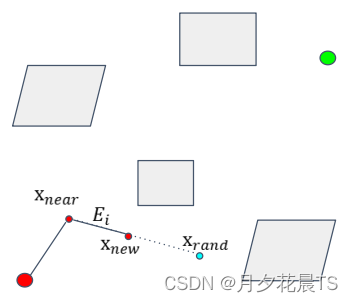
near点表示从RRT树 Γ Gamma Γ中通过距离函数，判断树中哪个点距离当前rand点最近，此时该点即为near点。对应于算法框架中的Near函数。

new点表示以near点到rand为方向，以 E i E_i Ei为步长，生成的一个新点。对应于算法框架的Steer函数。

2.3 安全性检查

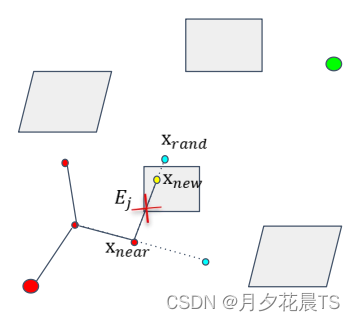
若上述的new点在安全区域内，且new与near点连线安全，则会在RRT树中进行扩展，否则不会进行扩展。对应于算法框架中的CollisionFree函数。

2.4 算法结束判断

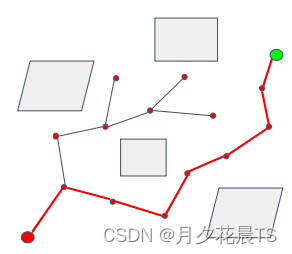
算法框架中的当new点与goal相等，表示算法运行成功，但是实际编程情况中，new点与goal点会存在一定的距离阈值。

3.RRT代码框架

3.1 主函数

main.cpp ：首先通过地图文件中读取地图数据(本次代码提供两张地图，供测试使用)，然后设置RRT算法的起点和终点，以及相关参数设置，例如距离阈值、步长、迭代次数等。其次通过RRT算法的接口函数RRTCore和CreatePath获得RRT算法的路径，最后通过显示函数Display进行数据可视化。

#include <iostream>
#include <vector>
#include <string>
#include "map.h"
#include "display.h"
#include "RRT.h"
using namespace std;
int main()
{
	//读取地图点
	//vector<vector<int>>mapData = MapData("map/map.txt");
	定义起点和终点,以及阈值
	//int xStart = 10;
	//int yStart = 10;
	//int xGoal = 700;
	//int yGoal = 700;
	//int thr = 50;
	//int delta = 30;
	//int numer = 3000;
	//读取地图点
	vector<vector<int>>mapData = MapData("map/map6.txt");
	//定义起点和终点,以及阈值
	int xStart = 134;       //起点x值
	int yStart = 161;       //起点y值
	int xGoal = 251;        //终点x值
	int yGoal = 61;         //终点y值
	int thr = 10;           //结束与终点的距离阈值
	int delta = 10;         //步长
	int numer = 3000;       //迭代参数
	//创建RRT对象
	CRRT rrt(xStart, yStart, xGoal, yGoal, thr, delta, mapData);
	vector<pair<float, float>>nearList, newList;
	vector<pair<int, int>>path;
	//RRT核心函数
	bool flag = rrt.RRTCore(nearList, newList,numer);
	if (flag == true)
	{
		//通过RRT获得路径
		rrt.CreatePath(path);
		std::cout << "path size is:" << path.size() << std::endl;
		//显示函数
		Display(xStart, yStart, xGoal, yGoal, mapData, path, nearList, newList);
	}
	return 0;
}

3.2 地图数据的获取

本次地图数据通过python程序将地图图片中的障碍物的位置存储起来，然后通过C++流的方式进行读取。

img2txt.py：该程序可以将彩蛇或者黑白地图中的障碍物**(gray_img [ i ] [ j ] [i][j] [i][j]== 0,数据0在图片中为纯黑，表示障碍物；255在图片中为纯白，表示自由可通行区域)**读取，然后以txt的格式进行存储。python程序需要opencv的环境，大家自己百度安装。

# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt # plt 用于显示图片
import numpy as np
import cv2
img = cv2.imread("map/map6.bmp")
print(img.shape)
if len(img.shape)==3:
    print("图片为彩色图")
    gray_img = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
elif len(img.shape)==2:
    print("图片为灰度图")
    gray_img=img
h=gray_img.shape[0]
w=gray_img.shape[1]
print (gray_img.shape)
f = open("map/map6.txt", "wb")
# 尺寸 h, w
f.write((str(h) + " " + str(w) + "
").encode("utf-8"))
for i in range(h):
    for j in range(w):
        if gray_img[i][j] == 0:
            print("hello  world")
            f.write((str(i) + " " + str(j) + "
").encode("utf-8"))

f.close()
print ("map.txt save sucessful")

其中保存的地图txt数据分为两部分，第一行表示地图的高和宽；从第二行开始表示障碍物的坐标值，例如234 648表示第648行，第234列那个点的图像像素值为0。图像坐标系中原点坐标在图像的左上角，x轴向右，y轴向下。

800 800
234 648
234 649
234 650
234 651
234 652
234 653
234 654
234 655
234 656
234 657
234 658
234 659
…

map.h

#pragma once
#ifndef __MAP__
#define __MAP__
#include <vector>
#include<iostream>
#include <string>
using namespace std;
vector<vector<int>> MapData(std::string _MapPath);

#endif

map.cpp：通过C++流的方式进行txt数据的读取，按照上述存储方式进行读取。

/*该函数是读取map.txt形成一个二维数组num，其中num里面0表示障碍物,255为可自由区域*/
#include "map.h"
#include<fstream>
#include<sstream>
vector<vector<int>>MapData(std::string _MapPath)
{
	ifstream f;
	f.open(_MapPath);
	string str;
	vector<vector<int> > num;
	bool  FirstLine = true;
	while (getline(f, str))      //读取1行并将它赋值给字符串str
	{
		if (FirstLine)
		{
			istringstream in(str);   // c++风格的串流的输入操作
			int a;
			in >> a;
			int height = a;
		    in >> a;
			int wight = a;
			num.resize(height, vector<int>(wight, 255));
			FirstLine = false;
		}
		else
		{
			istringstream input(str);   // c++风格的串流的输入操作
			vector<int> tmp;
			int a;
			while (input >> a)          //通过input将第一行的数据一个一个的输入给a
				tmp.push_back(a);
			num[tmp[0]][tmp[1]] = 0;
		}
	}
	return num;
}

3.3 RRT算法的实现

RRT.h：主要通过RRTCore函数实现RRT算法的本体，通过CreatePath函数获得RRT算法的路径。

#pragma once
#ifndef __RRT__
#define __RRT__
#include <iostream>
#include <string>
#include <vector>
#include <math.h>
#include "ctime"
#define N 999
#define pi 3.1415926

using namespace std;
//定义RRT搜索树结构
struct Tree
{
	float Sx;          //当前点的x值
	float Sy;          //当前点的y值           //new点
	float SxPrev;      //该点先前点的x值
	float SyPrev;      //该点先前点的x值       //near点
	float Sdist;       //near点与new点的距离
	int SindPrev;      //new点的索引
};
class CRRT
{
public:
	//RRT构造函数
	CRRT(int _xStart, int _yStart, int _xGoal, int _yGoal, int _thr, int _delta, vector<vector<int>>_map);
	//距离计算函数
	inline float GetDist(int _x1, int _y1, int _x2, int _y2);
	//与rand点距离较近的点在RRT树中的索引
	int GetMinIndex(int _x1, int _y1, vector<Tree>_T);
	//点的安全性判定
	inline bool FeasiblePoint(float _x, float _y, vector<vector<int>>_map);
	//near点与new点连线之间的碰撞检测
	bool CollisionChecking(vector<float> _startPose, vector<float> _goalPose, vector<vector<int>>_map);
	//RRT核心函数
	bool RRTCore(int _numer,vector<pair<float,float>>& _nearList, vector<pair<float, float>>& _newList);
	//RRT生成路径函数
	void CreatePath(vector<pair<int, int>>& _path);
private:
	vector<Tree> m_TreeList;       //RRT搜索树列表
	Tree m_tree;                   //RRT搜索树
	vector<vector<int>>m_map;      //二维地图

	int m_xStart;                  //起点X值
	int m_yStart;                  //起点Y值

	int m_xGoal;                   //终点X值
	int m_yGoal;                   //终点Y值

	int m_thr;                     //距离阈值
	int m_delta;                   //步长
	int m_mapWight;                //地图宽度
	int m_mapHight;                //地图高度
};

#endif

RRT.cpp：主要实现RRT.h头文件中的各成员函数。

#include "RRT.h"

/***********************************************************
*@函数功能:       RRT构造函数,对地图宽度和高度进行初始化
-----------------------------------------------------------
*@函数参数:       _xStart  起点X值
				  _yStart  起点Y值
				  _xGoal   终点X值
	              _yGoal   终点Y值
	              _thr     距离阈值
	              _delta   步长
	              _map     地图
-----------------------------------------------------------
*@函数返回:      无
***********************************************************/
CRRT::CRRT(int _xStart,
	      int _yStart,
	      int _xGoal,
	      int _yGoal,
	      int _thr,
	      int _delta,
	      vector<vector<int>>_map
):m_xStart(_xStart),m_yStart(_yStart),m_xGoal(_xGoal),m_yGoal(_yGoal),m_thr(_thr),m_delta(_delta),m_map(_map)
{
	m_mapWight = _map[0].size();
	m_mapHight = _map.size();
}

/***********************************************************
*@函数功能:       两点距离计算函数
-----------------------------------------------------------
*@函数参数:       _x1  第一个点X值
				  _y1  第一个点Y值
				  _x2  第二个点X值
				  _y2  第二个点Y值
-----------------------------------------------------------
*@函数返回:      两点之间的距离值
***********************************************************/
inline float CRRT::GetDist(int _x1, int _y1, int _x2, int _y2)
{
	return sqrt(pow((_x1 - _x2), 2) + pow((_y1 - _y2), 2));
}

/***********************************************************
*@函数功能:      求rand点距离较近的点在RRT树中的索引
-----------------------------------------------------------
*@函数参数:       _x1  rand点X值
				  _y1  rand点Y值
				  _T   RRT搜索树列表
-----------------------------------------------------------
*@函数返回:      最近索引值
***********************************************************/
int CRRT::GetMinIndex(int _x1, int _y1, vector<Tree>_T)
{
	float distance = FLT_MAX;            //FLT_MAX表示float最大值
	int index = 0;
	for (int i = 0; i < _T.size(); i++)
	{
		if (GetDist(_x1, _y1, _T[i].Sx, _T[i].Sy) < distance)
		{
			distance = GetDist(_x1, _y1, _T[i].Sx, _T[i].Sy);
			index = i;
		}
	}
	return index;
}

/***********************************************************
*@函数功能:      点的安全性判定
-----------------------------------------------------------
*@函数参数:       _x1  点X值
				  _y1  点Y值
                  _map 地图点
-----------------------------------------------------------
*@函数返回:      true表示该点安全,false表示不安全
***********************************************************/
inline bool CRRT::FeasiblePoint(float _x, float _y, vector<vector<int>>_map)
{
	//判断该点是否在地图的高度和宽度范围内,且是否在障碍物内
	if (!(_x >= 0 && _x < m_mapWight && _y >= 0 && _y < m_mapHight && _map[_y][_x] == 255))
		return false;
	return true;
}

/***********************************************************
*@函数功能:      near点与new点连线之间的碰撞检测
-----------------------------------------------------------
*@函数参数:       _startPose  near点
				  _goalPose   new点
                  _map 地图点
-----------------------------------------------------------
*@函数返回:      true表示安全,false表示不安全
***********************************************************/
bool CRRT::CollisionChecking(vector<float> _startPose, vector<float> _goalPose, vector<vector<int>>_map)
{
	//new点若在障碍物内,直接返回false
	if (!(FeasiblePoint(floor(_goalPose[0]), ceil(_goalPose[1]), _map)))
	{
		return false;
	}
	float dir = atan2(_goalPose[0] - _startPose[0], _goalPose[1] - _startPose[1]);
	float poseCheck[2] = { 0.0,0.0 };
	float stop = sqrt(pow(_startPose[0] - _goalPose[0], 2) + pow(_startPose[1] - _goalPose[1], 2));
	//r+=2表示在near与new连线的基础上,每次移动2个步长
	for (float r = 0; r <= stop; r += 2)
	{
		poseCheck[0] = _startPose[0] + r*sin(dir);
		poseCheck[1] = _startPose[1] + r*cos(dir);
		//由于poseCheck点为float类型,为亚像素级,因此判断该点四领域的像素值,ceil向上取整,floor向下取整
		if (!(FeasiblePoint(ceil(poseCheck[0]), ceil(poseCheck[1]), _map) &&
		FeasiblePoint(floor(poseCheck[0]), floor(poseCheck[1]), _map) &&
		FeasiblePoint(ceil(poseCheck[0]), floor(poseCheck[1]), _map) &&
		FeasiblePoint(floor(poseCheck[0]), ceil(poseCheck[1]), _map)))
		{
			return false;
		}
	}
	return true;
}

/***********************************************************
*@函数功能:   RRT核心函数
-----------------------------------------------------------
*@函数参数:   _nearList  near点集合,为引用传参,实际上也为返回值
			  _newList    new点集合,为引用传参,实际上也为返回值
			  _numer     RRT算法迭代次数
-----------------------------------------------------------
*@函数返回:   true表示RRT找到路径,false表示没找到
***********************************************************/
bool CRRT::RRTCore(int _numer,vector<pair<float, float>>& _nearList, vector<pair<float, float>>& _newList)
{
	//将起点插入树中
	m_tree.Sx =m_xStart;
	m_tree.Sy = m_yStart;
	m_tree.SxPrev = m_xGoal;
	m_tree.SyPrev = m_yGoal;
	m_tree.Sdist = 0;
	m_tree.SindPrev = 0;
	m_TreeList.push_back(m_tree);

	vector<float>Rand, Near, New;
	Rand.resize(2, 0.0);
	Near.resize(2, 0.0);
	New.resize(2, 0.0);

	srand(time(NULL));//设置随机数种子，使每次产生的随机序列不同
	int count = 0;
	for (int i = 1; i <= _numer; i++)
	{
		//随机产生地图点Rand
		Rand[0] =m_mapWight*(rand() % (N + 1) / (float)(N + 1));
		Rand[1] = m_mapHight*(rand() % (N + 1) / (float)(N + 1));

		//通过距离判断来计算与Rand最近的Near点
		int minDisIndex = GetMinIndex(Rand[0], Rand[1], m_TreeList);
		Near[0] = m_TreeList[minDisIndex].Sx;
		Near[1] = m_TreeList[minDisIndex].Sy;

		//Near与Rand连线,移动delta步长
		float theta = atan2(Rand[1] - Near[1], Rand[0] - Near[0]);
		New[0] = Near[0] + m_delta*(cos(theta));
		New[1] = Near[1] + m_delta*(sin(theta));

		//连线碰撞检测
		if (!CollisionChecking(Near, New, m_map))
			continue;

		//扩展RRT搜索树
		std::cout << "i:" << i << std::endl;
		m_tree.Sx = New[0];
		m_tree.Sy = New[1];
		m_tree.SxPrev = Near[0];
		m_tree.SyPrev = Near[1];
		m_tree.Sdist = m_delta;
		m_tree.SindPrev = minDisIndex;
		m_TreeList.emplace_back(m_tree);

		//距离阈值判断,是否搜索结束
		if (GetDist(New[0], New[1], m_xGoal, m_yGoal) < m_thr)
		{
			return true;
		}

		//保存near点与new点
		_nearList.emplace_back(std::make_pair(Near[0], Near[1]));
		_newList.emplace_back(std::make_pair(New[0], New[1]));
	}
	return false;

}

/***********************************************************
*@函数功能:   RRT生成路径,逆向搜索
-----------------------------------------------------------
*@函数参数:   _path  RRT生成路径集合点,为引用传参,实际上也为返回值
-----------------------------------------------------------
*@函数返回:   无
***********************************************************/
void CRRT::CreatePath(vector<pair<int, int>>& _path)
{
	pair<int, int>temp;
	//将终点加入路径集合点
	_path.push_back(std::make_pair(m_xGoal, m_yGoal));
	//由于搜索路径结束存在一个阈值,故将搜索树的最后一个点加入路径集合点
	_path.push_back(std::make_pair(m_TreeList[m_TreeList.size() - 1].Sx, m_TreeList[m_TreeList.size() - 1].Sy));

	int pathIndex = m_TreeList[m_TreeList.size() - 1].SindPrev;
	//逆向搜索
	while (true)
	{
		_path.emplace_back(std::make_pair(m_TreeList[pathIndex].Sx, m_TreeList[pathIndex].Sy));

		pathIndex = m_TreeList[pathIndex].SindPrev;
		if (pathIndex == 0)
			break;
	}
	//将起点加入路径集合点
	_path.push_back(std::make_pair(m_TreeList[0].Sx, m_TreeList[0].Sy));

}

接下里主要从RRT中的核心函数RRTCore进行算法介绍。

3.3.1 起点入树

#include "RRT.h"
/***********************************************************
*@函数功能:       RRT构造函数,对地图宽度和高度进行初始化
-----------------------------------------------------------
*@函数参数:       _xStart  起点X值
				  _yStart  起点Y值
				  _xGoal   终点X值
	              _yGoal   终点Y值
	              _thr     距离阈值
	              _delta   步长
	              _map     地图
-----------------------------------------------------------
*@函数返回:      无
***********************************************************/
CRRT::CRRT(int _xStart,
	      int _yStart,
	      int _xGoal,
	      int _yGoal,
	      int _thr,
	      int _delta,
	      vector<vector<int>>_map
):m_xStart(_xStart),m_yStart(_yStart),m_xGoal(_xGoal),m_yGoal(_yGoal),m_thr(_thr),m_delta(_delta),m_map(_map)
{
	m_mapWight = _map[0].size();
	m_mapHight = _map.size();
}
/***********************************************************
*@函数功能:       两点距离计算函数
-----------------------------------------------------------
*@函数参数:       _x1  第一个点X值
				  _y1  第一个点Y值
				  _x2  第二个点X值
				  _y2  第二个点Y值
-----------------------------------------------------------
*@函数返回:      两点之间的距离值
***********************************************************/
inline float CRRT::GetDist(int _x1, int _y1, int _x2, int _y2)
{
	return sqrt(pow((_x1 - _x2), 2) + pow((_y1 - _y2), 2));
}
/***********************************************************
*@函数功能:      求rand点距离较近的点在RRT树中的索引
-----------------------------------------------------------
*@函数参数:       _x1  rand点X值
				  _y1  rand点Y值
				  _T   RRT搜索树列表
-----------------------------------------------------------
*@函数返回:      最近索引值
***********************************************************/
int CRRT::GetMinIndex(int _x1, int _y1, vector<Tree>_T)
{
	float distance = FLT_MAX;            //FLT_MAX表示float最大值
	int index = 0;
	for (int i = 0; i < _T.size(); i++)
	{
		if (GetDist(_x1, _y1, _T[i].Sx, _T[i].Sy) < distance)
		{
			distance = GetDist(_x1, _y1, _T[i].Sx, _T[i].Sy);
			index = i;
		}
	}
	return index;
}
/***********************************************************
*@函数功能:      点的安全性判定
-----------------------------------------------------------
*@函数参数:       _x1  点X值
				  _y1  点Y值
                  _map 地图点
-----------------------------------------------------------
*@函数返回:      true表示该点安全,false表示不安全
***********************************************************/
inline bool CRRT::FeasiblePoint(float _x, float _y, vector<vector<int>>_map)
{
	//判断该点是否在地图的高度和宽度范围内,且是否在障碍物内
	if (!(_x >= 0 && _x < m_mapWight && _y >= 0 && _y < m_mapHight && _map[_y][_x] == 255))
		return false;
	return true;
}
/***********************************************************
*@函数功能:      near点与new点连线之间的碰撞检测
-----------------------------------------------------------
*@函数参数:       _startPose  near点
				  _goalPose   new点
                  _map 地图点
-----------------------------------------------------------
*@函数返回:      true表示安全,false表示不安全
***********************************************************/
bool CRRT::CollisionChecking(vector<float> _startPose, vector<float> _goalPose, vector<vector<int>>_map)
{
	//new点若在障碍物内,直接返回false
	if (!(FeasiblePoint(floor(_goalPose[0]), ceil(_goalPose[1]), _map)))
	{
		return false;
	}
	float dir = atan2(_goalPose[0] - _startPose[0], _goalPose[1] - _startPose[1]);
	float poseCheck[2] = { 0.0,0.0 };
	float stop = sqrt(pow(_startPose[0] - _goalPose[0], 2) + pow(_startPose[1] - _goalPose[1], 2));
	//r+=2表示在near与new连线的基础上,每次移动2个步长
	for (float r = 0; r <= stop; r += 2)
	{
		poseCheck[0] = _startPose[0] + r*sin(dir);
		poseCheck[1] = _startPose[1] + r*cos(dir);
		//由于poseCheck点为float类型,为亚像素级,因此判断该点四领域的像素值,ceil向上取整,floor向下取整
		if (!(FeasiblePoint(ceil(poseCheck[0]), ceil(poseCheck[1]), _map) &&
		FeasiblePoint(floor(poseCheck[0]), floor(poseCheck[1]), _map) &&
		FeasiblePoint(ceil(poseCheck[0]), floor(poseCheck[1]), _map) &&
		FeasiblePoint(floor(poseCheck[0]), ceil(poseCheck[1]), _map)))
		{
			return false;
		}
	}
	return true;
}
/***********************************************************
*@函数功能:   RRT核心函数
-----------------------------------------------------------
*@函数参数:   _nearList  near点集合,为引用传参,实际上也为返回值
			  _newList    new点集合,为引用传参,实际上也为返回值
			  _numer     RRT算法迭代次数
-----------------------------------------------------------
*@函数返回:   true表示RRT找到路径,false表示没找到
***********************************************************/
bool CRRT::RRTCore(int _numer,vector<pair<float, float>>& _nearList, vector<pair<float, float>>& _newList)
{
	//将起点插入树中
	m_tree.Sx =m_xStart;
	m_tree.Sy = m_yStart;
	m_tree.SxPrev = m_xGoal;
	m_tree.SyPrev = m_yGoal;
	m_tree.Sdist = 0;
	m_tree.SindPrev = 0;
	m_TreeList.push_back(m_tree);
	vector<float>Rand, Near, New;
	Rand.resize(2, 0.0);
	Near.resize(2, 0.0);
	New.resize(2, 0.0);
	srand(time(NULL));//设置随机数种子，使每次产生的随机序列不同
	int count = 0;
	for (int i = 1; i <= _numer; i++)
	{
		//随机产生地图点Rand
		Rand[0] =m_mapWight*(rand() % (N + 1) / (float)(N + 1));
		Rand[1] = m_mapHight*(rand() % (N + 1) / (float)(N + 1));
		//通过距离判断来计算与Rand最近的Near点
		int minDisIndex = GetMinIndex(Rand[0], Rand[1], m_TreeList);
		Near[0] = m_TreeList[minDisIndex].Sx;
		Near[1] = m_TreeList[minDisIndex].Sy;
		//Near与Rand连线,移动delta步长
		float theta = atan2(Rand[1] - Near[1], Rand[0] - Near[0]);
		New[0] = Near[0] + m_delta*(cos(theta));
		New[1] = Near[1] + m_delta*(sin(theta));
		//连线碰撞检测
		if (!CollisionChecking(Near, New, m_map))
			continue;
		//扩展RRT搜索树
		std::cout << "i:" << i << std::endl;
		m_tree.Sx = New[0];
		m_tree.Sy = New[1];
		m_tree.SxPrev = Near[0];
		m_tree.SyPrev = Near[1];
		m_tree.Sdist = m_delta;
		m_tree.SindPrev = minDisIndex;
		m_TreeList.emplace_back(m_tree);
		//距离阈值判断,是否搜索结束
		if (GetDist(New[0], New[1], m_xGoal, m_yGoal) < m_thr)
		{
			return true;
		}
		//保存near点与new点
		_nearList.emplace_back(std::make_pair(Near[0], Near[1]));
		_newList.emplace_back(std::make_pair(New[0], New[1]));
	}
	return false;
}
/***********************************************************
*@函数功能:   RRT生成路径,逆向搜索
-----------------------------------------------------------
*@函数参数:   _path  RRT生成路径集合点,为引用传参,实际上也为返回值
-----------------------------------------------------------
*@函数返回:   无
***********************************************************/
void CRRT::CreatePath(vector<pair<int, int>>& _path)
{
	pair<int, int>temp;
	//将终点加入路径集合点
	_path.push_back(std::make_pair(m_xGoal, m_yGoal));
	//由于搜索路径结束存在一个阈值,故将搜索树的最后一个点加入路径集合点
	_path.push_back(std::make_pair(m_TreeList[m_TreeList.size() - 1].Sx, m_TreeList[m_TreeList.size() - 1].Sy));
	int pathIndex = m_TreeList[m_TreeList.size() - 1].SindPrev;
	//逆向搜索
	while (true)
	{
		_path.emplace_back(std::make_pair(m_TreeList[pathIndex].Sx, m_TreeList[pathIndex].Sy));
		pathIndex = m_TreeList[pathIndex].SindPrev;
		if (pathIndex == 0)
			break;
	}
	//将起点加入路径集合点
	_path.push_back(std::make_pair(m_TreeList[0].Sx, m_TreeList[0].Sy));

}

3.3.2 rand点的获取

为了方便起见，并没有设置随机采样函数，通过随机种子进行rand的确定。其中(rand() % (N + 1) / (float)(N + 1))是产生0~1的随机树，小数点与N有关。

m_tree.Sx =m_xStart;
m_tree.Sy = m_yStart;
m_tree.SxPrev = m_xGoal;
m_tree.SyPrev = m_yGoal;
m_tree.Sdist = 0;
m_tree.SindPrev = 0;
m_TreeList.push_back(m_tree);
vector<float>Rand, Near, New;
Rand.resize(2, 0.0);
Near.resize(2, 0.0);
New.resize(2, 0.0);

3.3.3 near点的获取

通过简单的距离函数进行near点的判断。其中GetMinIndex就是通过遍历获取与rand点最近的near点，当然可以通过kd-tree对这块进行改进，大家感兴趣可以自行发挥，这里为了方便起见，就采用最原始的方法。

//随机产生地图点Rand
Rand[0] =m_mapWight*(rand() % (N + 1) / (float)(N + 1));
Rand[1] = m_mapHight*(rand() % (N + 1) / (float)(N + 1));

3.3.4 new点的获取

//通过距离判断来计算与Rand最近的Near点
int minDisIndex = GetMinIndex(Rand[0], Rand[1], m_TreeList);
Near[0] = m_TreeList[minDisIndex].Sx;
Near[1] = m_TreeList[minDisIndex].Sy;

注意near点的获取使用C++中的atan2函数，该函数是 atan() 的增强版，能够确定角度所在的象限。

其中**double atan2(double y，double x)**返回 y/x 的反正切值，以弧度表示，取值范围为(-π,π]。如下图所示，红色线为 s i n ( θ ) sin( heta) sin(θ)，绿色线为 c o s ( θ ) cos( heta) cos(θ)。

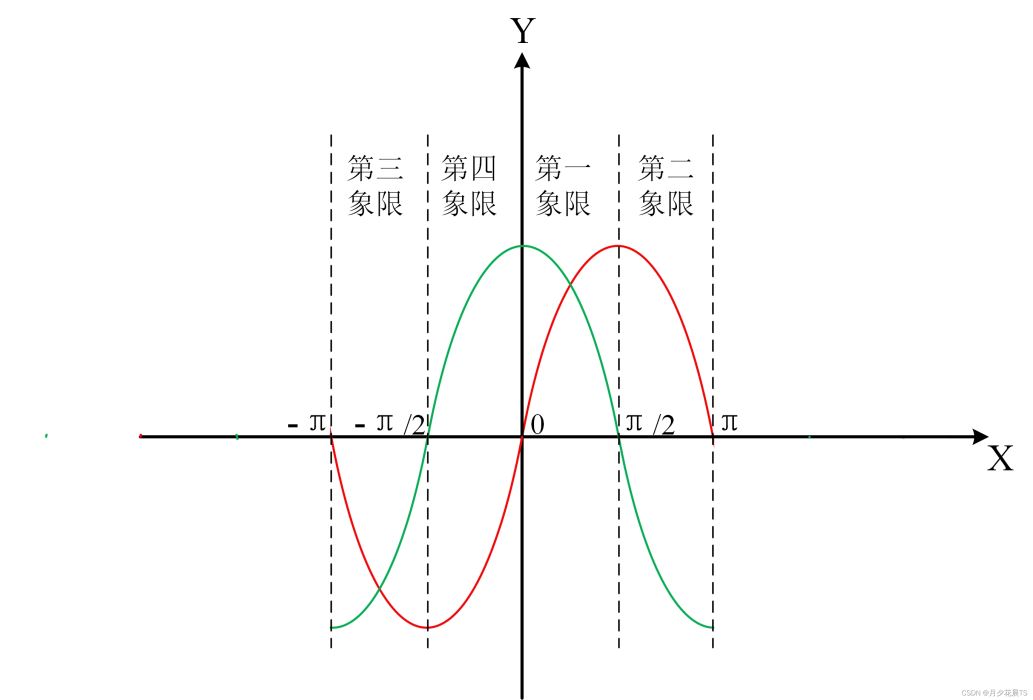
当 (x, y) 在象限中时：

第一象限

第二象限

第三象限

第四象限

0 < θ < π / 2 0< heta<pi/2 0<θ<π/2

π / 2 < θ < π pi/2 < heta <pi π/2<θ<π

π < θ < π / 2 -pi< heta<-pi/2 π<θ<π/2

π / 2 < θ < 0 -pi/2< heta<0 π/2<θ<0

当 (x, y) 在象限的边界（也就是坐标轴）上时：

y = 0 y=0 y=0且 x ≥ 0 x geq 0 x≥0

y = 0 y=0 y=0且 x < 0 x < 0 x<0

y > 0 y>0 y>0且 x = 0 x=0 x=0

y < 0 y<0 y<0且 x = 0 x=0 x=0

θ = 0 heta =0 θ=0

θ = π heta=pi θ=π

θ = π / 2 heta=pi/2 θ=π/2

θ = π / 2 heta=-pi/2 θ=π/2

那么
n e w _ x = n e a r _ x + d c o s ( θ ) n e w _ y = n e a e _ y + d s i n ( θ ) new_x=near_x+d*cos( heta) \ new_y=neae_y+d*sin( heta) \ new_x=near_x+dcos(θ)new_y=neae_y+dsin(θ)

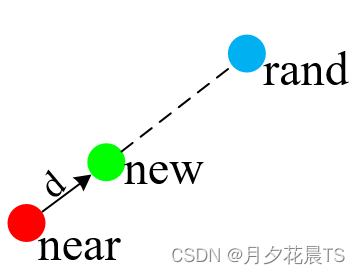
表示new点的情况如下，均满足new点在near与rand点之间。这就是atan2带来的好处。

第一象限

第二象限

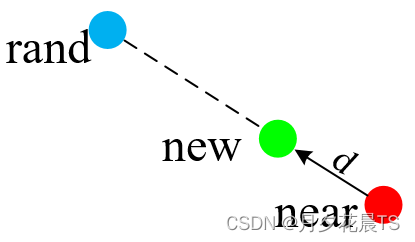
第三象限

第四象限

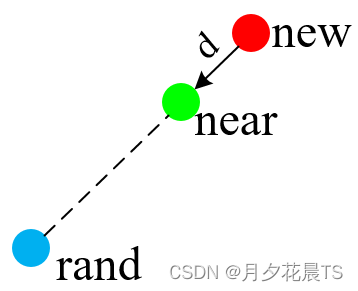
3.3.5 安全性检测

near点与new点之间的安全性判断通过CollisionChecking函数所实习，基本思想就是沿着near与new点的方向，每隔一定的微小步长（代码中用 r r r）取一点，判断该点是否在障碍物内。注意微小步长所取的点，它的像素是亚像素级的，可通过双线性插值方法判断该像素的值。本文为了方便起见，判断该点亚像素的周围四点领域，进行安全性判断。

举个例子，例如该点为 p = ( 1.3 , 4.7 ) p=(1.3,4.7) p=(1.3,4.7)，通过向下取整floor和向上取整ceil得该亚像素点的四点领域

c e i l ( 1.3 ) = 2 , c e i l ( 4.7 ) = 5 > p 1 = ( 2 , 5 ) ceil(1.3)=2,ceil(4.7) =5 —>p_1=(2,5) ceil(1.3)=2,ceil(4.7)=5>p1=(2,5)

f l o o r ( 1.3 ) = 1 , f l o o r ( 4.7 ) = 4 > p 2 = ( 1 , 4 ) floor(1.3)=1,floor(4.7)=4–>p_2=(1,4) floor(1.3)=1,floor(4.7)=4>p2=(1,4)

c e i l ( 1.3 ) = 2 , f l o o r ( 4.7 ) = 4 > p 3 = ( 2 , 4 ) ceil(1.3)=2,floor(4.7)=4–>p_3=(2,4) ceil(1.3)=2,floor(4.7)=4>p3=(2,4)

f l o o r ( 1.3 ) = 1 , c e i l ( 4.7 ) = 5 > p 4 = ( 1 , 5 ) floor(1.3)=1,ceil(4.7) =5—>p_4=(1,5) floor(1.3)=1,ceil(4.7)=5>p4=(1,5)

bool CRRT::CollisionChecking(vector<float> _startPose, vector<float> _goalPose, vector<vector<int>>_map)
{
	//new点若在障碍物内,直接返回false
	if (!(FeasiblePoint(floor(_goalPose[0]), ceil(_goalPose[1]), _map)))
	{
		return false;
	}
	float dir = atan2(_goalPose[0] - _startPose[0], _goalPose[1] - _startPose[1]);
	float poseCheck[2] = { 0.0,0.0 };
	float stop = sqrt(pow(_startPose[0] - _goalPose[0], 2) + pow(_startPose[1] - _goalPose[1], 2));
	//r+=2表示在near与new连线的基础上,每次移动2个步长
	for (float r = 0; r <= stop; r += 2)
	{
		poseCheck[0] = _startPose[0] + r*sin(dir);
		poseCheck[1] = _startPose[1] + r*cos(dir);
		//由于poseCheck点为float类型,为亚像素级,因此判断该点四领域的像素值,ceil向上取整,floor向下取整
		if (!(FeasiblePoint(ceil(poseCheck[0]), ceil(poseCheck[1]), _map) &&
		FeasiblePoint(floor(poseCheck[0]), floor(poseCheck[1]), _map) &&
		FeasiblePoint(ceil(poseCheck[0]), floor(poseCheck[1]), _map) &&
		FeasiblePoint(floor(poseCheck[0]), ceil(poseCheck[1]), _map)))
		{
			return false;
		}
	}
	return true;
}

3.4 可视化显示

display.h

#pragma once
#ifndef __DISPLAY__
#define __DISPLAY__
#include <opencv2/opencv.hpp>
#include <vector>
using namespace std;
//显示函数
void Display(int _xStart,int _yStart,int _xGoal,int _yGoal,
	         vector<vector<int>>_map,
	         vector<pair<int, int>>_path,
	         vector<pair<float, float>>_nearList,
	         vector<pair<float, float>>_newList);
#endif // !__DISPLAY__

display.cpp

注意该代码会在当前项目中的image文件夹(没有该文件夹，手动创建一个即可)中存储rrt显示过程图片(为了后期作gif使用，其他没什么用)，若是不想存储，则注释掉。

cv::imwrite(“image/image” + std::to_string(i) + “.jpg”, image);

#include "display.h"
#include <iostream>
#include <string>
#include <Windows.h>
#include <cstdlib>
#include <io.h>      // _access
#include <direct.h>  //_mkdir
/***********************************************************
*@函数功能:       RRT函数显示
-----------------------------------------------------------
*@函数参数:       _xStart  起点X值
				  _yStart  起点Y值
				  _xGoal   终点X值
                  _yGoal   终点Y值
                  _thr     距离阈值
                  _map     地图
				  _path    路径点
				  _nearList near点集合
				  _newList  new点集合
-----------------------------------------------------------
*@函数返回:      无
***********************************************************/
void Display(int _xStart,
	         int _yStart,
	         int _xGoal,
	         int _yGoal,
	         vector<vector<int>>_map,
	         vector<pair<int, int>>_path,
	         vector<pair<float, float>>_nearList,
	         vector<pair<float, float>>_newList)
{
	int mapWight = _map[0].size();
	int mapHight = _map.size();

	//如没有image文件夹,则新建一个,存放RRT扩展树的中间过程
	std::string prefix = "image";
	if (_access(prefix.c_str(), 0) == -1)	//如果文件夹不存在
	{
		_mkdir(prefix.c_str());    //则创建
	}

	//通过地图点绘制图像RGB,白色可通行区域,黑色为障碍物区域
	cv::namedWindow("RRT result", CV_WINDOW_AUTOSIZE);
	cv::Mat image(mapHight, mapWight, CV_8UC3, cv::Scalar(0, 0, 0));
	for (int row = 0; row < mapHight; row++)
	{
		for (int col = 0; col < mapWight; col++)
		{
			if (_map[row][col] == 255)
			{
				image.at<cv::Vec3b>(row, col)[0] = 255;
				image.at<cv::Vec3b>(row, col)[1] = 255;
				image.at<cv::Vec3b>(row, col)[2] = 255;
			}
		}
	}
	//显示起点和终点,红色起点,绿色终点
	cv::circle(image, cv::Point(_xStart, _yStart), 4, cv::Scalar(0, 0, 255), -1, 4);   //起点
	cv::circle(image, cv::Point(_xGoal, _yGoal), 4, cv::Scalar(0, 255, 0), -1, 4);    //终点

	//显示路径探索过程
	for (int i = 0; i < _nearList.size(); i++)
	{
		cv::line(image, cv::Point(_nearList[i].first, _nearList[i].second), cv::Point(_newList[i].first, _newList[i].second), cv::Scalar(255, 0, 0), 2, 2);
		cv::imshow("RRT result", image);
		cv::waitKey(100);  //100ms刷新一下
		cv::imwrite("image/image" + std::to_string(i) + ".jpg", image);
	}
	//显示最终路径,黄色
	for (int i = 0; i < _path.size() - 1; i++)
	{
		cv::line(image, cv::Point(_path[i].first, _path[i].second), cv::Point(_path[i + 1].first, _path[i + 1].second), cv::Scalar(0, 255, 255), 2, 2);
	}
	//保存6张最终图片,方便制作gif
	for (int i = 0; i <= 5; i++)
	{
	    cv::imwrite("image/image"+std::to_string(_nearList.size()+i)+".jpg", image);
	}
	cv::imshow("RRT result", image);
	cv::waitKey(0);
}

4. 代码运行过程

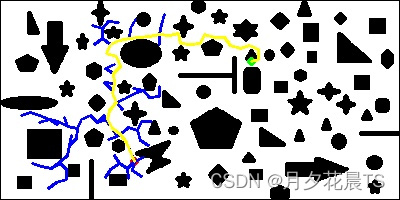
注意显示过程中的“树枝”表示near点与new点的连接。

显示过程

显示结果

map6.bmp

显示过程

显示结果

map.png

<动图太大，CSDN仅支持5M，无法显示>

一个批量将图片转为gif的python脚本，注意python代码中一定要添加dir_list = natsort.natsorted(dir_list)，否则会出现图片乱序的问题。

import os
import cv2 as cv
import moviepy.editor as mpy
import numpy as np
import natsort
import imageio
def frame_to_gif(frame_list):
    gif = imageio.mimsave('./result.gif', frame_list, 'GIF', duration=0.00085)
dir_list = os.listdir('image')
dir_list = natsort.natsorted(dir_list)
img_list=[]
for i in range(0,len(dir_list)):
    print (dir_list[i])
    img = cv.imread('image\' + dir_list[i])
    #img = cv.cvtcolor(img, cv.color_bgr2rgb)
    img_list.append(img)
frame_to_gif(img_list)

到此这篇关于C++结合OpenCV实现RRT算法的文章就介绍到这了,更多相关C++ OpenCV RRT算法内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！