python中sympy库求常微分方程的用法

问题1：

程序，如下

from sympy import *
f = symbols('f', cls=Function)
x = symbols('x')
eq = Eq(f(x).diff(x, x) - 2*f(x).diff(x) + f(x), sin(x))
print(dsolve(eq, f(x)))

结果

Eq(f(x), (C1 + C2*x)*exp(x) + cos(x)/2)

附：布置考试中两题

1.利用python的Sympy库求解微分方程的解 y=f(x)，并尝试利用matplotlib绘制函数图像

程序，如下

from sympy import *
f = symbols('f', cls=Function)
x = symbols('x')
eq = Eq(f(x).diff(x,1)+f(x)+f(x)**2, 0)
print(dsolve(eq, f(x)))
C1 = symbols('C1')
eqr = -C1/(C1 - exp(x))
eqr1 = eqr.subs(x, 0)
print(solveset(eqr1 - 1, C1))
eqr2 = eqr.subs(C1, 1/2)
# 画图
import matplotlib.pyplot as plt
import numpy as np
x_1 = np.arange(-5, 5, 0.1)
y_1 = [-0.5/(0.5 - exp(x)) for x in x_1]
plt.plot(x_1, y_1)
plt.axis([-6,6,-10,10])
plt.grid()
plt.show()

结果

Eq(f(x), -C1/(C1 - exp(x)))
FiniteSet(1/2)

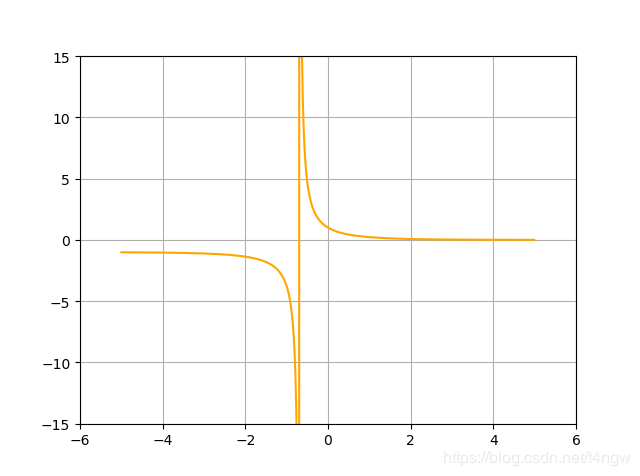
2.利用python的Sympy库求解微分方程的解 y=y(x)，并尝试利用matplotlib绘制函数图像

程序，如下

from sympy import *
y = symbols('y', cls=Function)
x = symbols('x')
eq = Eq(y(x).diff(x,1), y(x))
print(dsolve(eq, y(x)))
C1 = symbols('C1')
eqr = C1*exp(x)
eqr1 = eqr.subs(x, 0)
print(solveset(eqr1 - 1, C1))
eqr2 = eqr.subs(C1, 1)
# 画图
import matplotlib.pyplot as plt
import numpy as np
x_1 = np.arange(-5, 5, 0.01)
y_1 = [exp(x) for x in x_1]
plt.plot(x_1, y_1, color='orange')
plt.grid()
plt.show()

结果

Eq(y(x), C1*exp(x))
FiniteSet(1)

到此这篇关于python中sympy库求常微分方程的用法的文章就介绍到这了,更多相关python sympy常微分方程内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！

赞 (0)

相关推荐

  • Python Sympy计算梯度、散度和旋度的实例

    sympy有个vector 模块,里面提供了求解标量场.向量场的梯度.散度.旋度等计算,官方参考连接: http://docs.sympy.org/latest/modules/vector/index.html sympy中计算梯度.散度和旋度主要有两种方式: 一个是使用∇∇算子,sympy提供了类Del(),该类的方法有:cross.dot和gradient,cross就是叉乘,计算旋度的,dot是点乘,用于计算散度,gradient自然就是计算梯度的. 另一种方法就是直接调用相关的API:

  • 使用Python的SymPy库解决数学运算问题的方法

    摘要:在学习与科研中,经常会遇到一些数学运算问题,使用计算机完成运算具有速度快和准确性高的优势.Python的Numpy包具有强大的科学运算功能,且具有其他许多主流科学计算语言不具备的免费.开源.轻量级和灵活的特点.本文使用Python语言的NumPy库,解决数学运算问题中的线性方程组问题.积分问题.微分问题及矩阵化简问题,结果准确快捷,具有一定的借鉴意义. 1.Sympy库简介 SymPy一个用于符号型数学计算(symbolic mathematics)的Python库.它旨在成为一个功能齐全

  • python使用pip安装SciPy、SymPy、matplotlib教程

    背景: 使用pip install SciPy的格式安装python函数库SciPy的时候,发现老是报错,从网上找信息也没找到合适的解决办法,最后使用whl格式文件安装成功. 过程: 本人事先电脑安装了python3.5.2,电脑是64位的. 下载函数库:从网址http://www.lfd.uci.edu/~gohlke/pythonlibs/下载对应函数库的whl文件.注意下载对应的python版本和windows版本的whl文件,这里讲一下文件的规则:scipy‑0.19.1‑cp35‑cp

  • python/sympy求解矩阵方程的方法

    sympy版本:1.2 假设求解矩阵方程 AX=A+2X 其中 求解之前对矩阵方程化简为 (A−2E)X=A 令 B=(A−2E) 使用qtconsole输入下面程序进行求解 In [26]: from sympy import * In [27]: from sympy.abc import * In [28]: A=Matrix([[4,2,3],[1,1,0],[-1,2,3]]) In [29]: A Out[29]: Matrix([ [ 4, 2, 3], [ 1, 1, 0], [

  • Python数据处理篇之Sympy系列(五)---解方程

    Python数据处理篇之Sympy系列(五)---解方程

    前言 sympy不仅在符号运算方面强大,在解方程方面也是很强大. 本章节学习对应官网的:Solvers 官方教程 https://docs.sympy.org/latest/tutorial/solvers.html (一)求解多元一次方程-solve() 1.说明: 解多元一次方程可以使用solve(),在sympy里,等式是用Eq()来表示, 例如:2x=42x=4 表示为:Eq(x*2, 4) 2.源代码: """ 解下列二元一次方程 2x-y=3 3x+y=7 &qu

  • 利用Python的sympy包求解一元三次方程示例

    环境说明:Python3.7.2+Jupyter Notebook 示例1(求解一元三次方程): import sympy as sp # 导入sympy包 x = sp.Symbol('x') # 定义符号变量 f = x**3 - 3*x**2 + 3*x - 9/16 # 定义要求解的一元三次方程 x = sp.solve(f) # 调用solve函数求解方程 x # solve函数的返回结果是一个列表 # x的值为[0.240852757031084,1.37957362148446-0

  • python中sympy库求常微分方程的用法

    问题1: 程序,如下 from sympy import * f = symbols('f', cls=Function) x = symbols('x') eq = Eq(f(x).diff(x, x) - 2*f(x).diff(x) + f(x), sin(x)) print(dsolve(eq, f(x))) 结果 Eq(f(x), (C1 + C2*x)*exp(x) + cos(x)/2) 附:布置考试中两题 1.利用python的Sympy库求解微分方程的解 y=f(x),并尝试利

  • 详解python中mongoengine库用法

    详解python中mongoengine库用法

    目录 一.MongoDB的安装与连接 二.MongoEngine模型介绍 2.1.ODM模型介绍 2.2.常见数据类型 2.3.数据类型通用参数 2.4.类属性meta常见配置项 2.5.文档的嵌套模型 三.添加数据 3.1.方式一 3.2.方式二:使用create()方法 四.查询数据 4.1.单个文档查询 4.2.条件查询 4.3.聚合统计 4.4.排序 4.5.分页处理 五.修改和删除数据 5.1.修改数据 5.2.删除数据 一.MongoDB的安装与连接 安装:pip install m

  • python中pycurl库的用法实例

    本文实例讲述了python中pycurl库的用法,分享给大家供大家参考. 该实例代码实现从指定网址读取网页,主要是pycurl库的使用. 具体实现方法如下: #定义一个类 class CallBack: """ for pycurl """ def __init__(self): """Constructor""" self.data = "" def func(se

  • Python中optparser库用法实例详解

    本文研究的主要是Python中optparser库的相关内容,具体如下. 一直以来对optparser不是特别的理解,今天就狠下心,静下心研究了一下这个库.当然了,不敢说理解的很到位,但是足以应付正常的使用了.废话不多说,开始今天的分享吧. 简介 optparse模块主要用来为脚本传递命令参数功能. 引入 在IDE中引入optparser是很方便的. from optparser import OptionParser 初始化 相对而言,初始化需要我们多注意一点点了. 因为我们有两种不同的方式来

  • python中xlutils库用法浅析

    不少小伙伴认为,直接去操作excel,比我们利用各种代码数据去处理,直接又简单,不那么花里胡哨,但是在代码上,处理数据,直接的软件操作是行不通的,需要我们去利用代码去处理,其实解决麻烦的办法非常简单,只需要我们调用专业的处理数据的模块,就可以轻松处理了,比如excel处理中的xlutils库,下面详细为大家介绍使用. 简单介绍: 最常见的使用在excel中的复制. 安装方式: pip install xlutils 注意点: 虽然可以进行excel的复制.但是只能提供写操作,不能够复制格式. 使

  • python中doctest库实例用法

    doctest库就是一个测试用的标准库,从意义上我们可以看出是关于测试有关系的,基本上就是测试是否和自己想要的结果是否一致,经常能在编写文档时候进行使用,之前也给大家介绍过开发工具中unittest单元测试的使用,同理之下,本章内容也是非常简单的,下面小编就用全面,简洁,实用来介绍,作为初学者们的知识字典库. 语言使用: python -m doctest 语法: doctest.testmod() 实例应用: >>> # comments are ignored >>>

  • python中Mako库实例用法

    Mako是一个模板库.一种嵌入式的语言,能够实现简化组件布局以及继承,主要的用途也是和作用域有关,但是效果是最直接切灵活的,这些都是mako的基本功能,掌握了基础内容,接下来就是详细的了解讲述,从几个方面为大家详细讲述,首先在众多模板库中的优点,以及实例应用等等,一起来了解学习下吧. Mako的优点: 学习成本低,能够在结构上进行转义. 应用方向: 文本文件生成. 模块引用: from mako.template import Template 基本用法: from mako.template

  • python中PyQuery库用法分享

    python中PyQuery库用法分享

    PyQuery库就是python中的一个解析库.作用十分强大,使用上也是相当的灵活,能够实现初始化字符串.初始化 HTML 文件.初始化请求响应等多种场景,另外,本身中的CSS选择器,也是经常被大家使用的对象,结合以上的大致内容总结,接下来,我们一起详细的了解使用内容. 安装: >>> pip3 install pyquery 引用方法: from pyquery import PyQuery as pq CSS选择器: from pyquery import PyQuery as pq

  • Python中selenium库的用法详解

    selenium主要是用来做自动化测试,支持多种浏览器,爬虫中主要用来解决JavaScript渲染问题. 模拟浏览器进行网页加载,当requests,urllib无法正常获取网页内容的时候 一.声明浏览器对象 注意点一,Python文件名或者包名不要命名为selenium,会导致无法导入 from selenium import webdriver #webdriver可以认为是浏览器的驱动器,要驱动浏览器必须用到webdriver,支持多种浏览器,这里以Chrome为例 browser = w

  • Python 中拼音库 PyPinyin 用法详解

    最近碰到了一个问题,项目中很多文件都是接手过来的中文命名的一些素材,结果在部署的时候文件名全都乱码了,导致项目无法正常运行. 后来请教了一位大佬怎么解决文件名乱码的问题,他说这个需要正面解决吗?不需要,把文件名全部改掉,文件名永远不要用中文,永远不要. 我想他这么说的话,一定也是凭经验得出来的. 这里也友情提示大家,项目里面文件永远不要用中文,永远不要! 好,那不用中文用啥?平时来看,一般我们都会用英文来命名,一般也不会出现中文,比如 resource, controller, result,

随机推荐