C++递归算法处理岛屿问题详解

目录

• 岛屿问题定义
• 例题一-岛屿的数量
• 例题二-岛屿的周长

岛屿问题定义

岛屿问题是指用二维数组进行模拟， 1的位置表示陆地， 0的位置表示海洋。岛屿是指 被水（0）包围的陆地（1） 如下图所示：

岛屿问题是一道典型的递归问题（一位大佬曾说将岛屿问题看成是4叉树，我觉得这个比喻非常好）， 对每个陆地位置， 我们需要递归地检测它的上下左右位置是不是陆地。

下面我们来写一下对岛屿问题的递归模板：

    public void dfs(char[][] grid, int m, int n){
    	// 位置越界 或者 该位置已经被遍历过
        if(isBeyond(grid, m, n) || grid[m][n] == 2){
            return;
        }
        // 相应操作
        ........
        // 记录已经遍历过位置
        grid[m][n] = '2';
		// 递归遍历该陆地位置的上下左右位置
        dfs(grid, m-1, n);
        dfs(grid, m+1, n);
        dfs(grid, m, n-1);
        dfs(grid, m, n+1);
    }
	// 检测越界的函数
    boolean isBeyond(char[][] grid, int m, int n){
        if(m < 0 || m>=grid.length || n<0 || n>=grid[0].length){
            return true;
        }
        return false;
    }

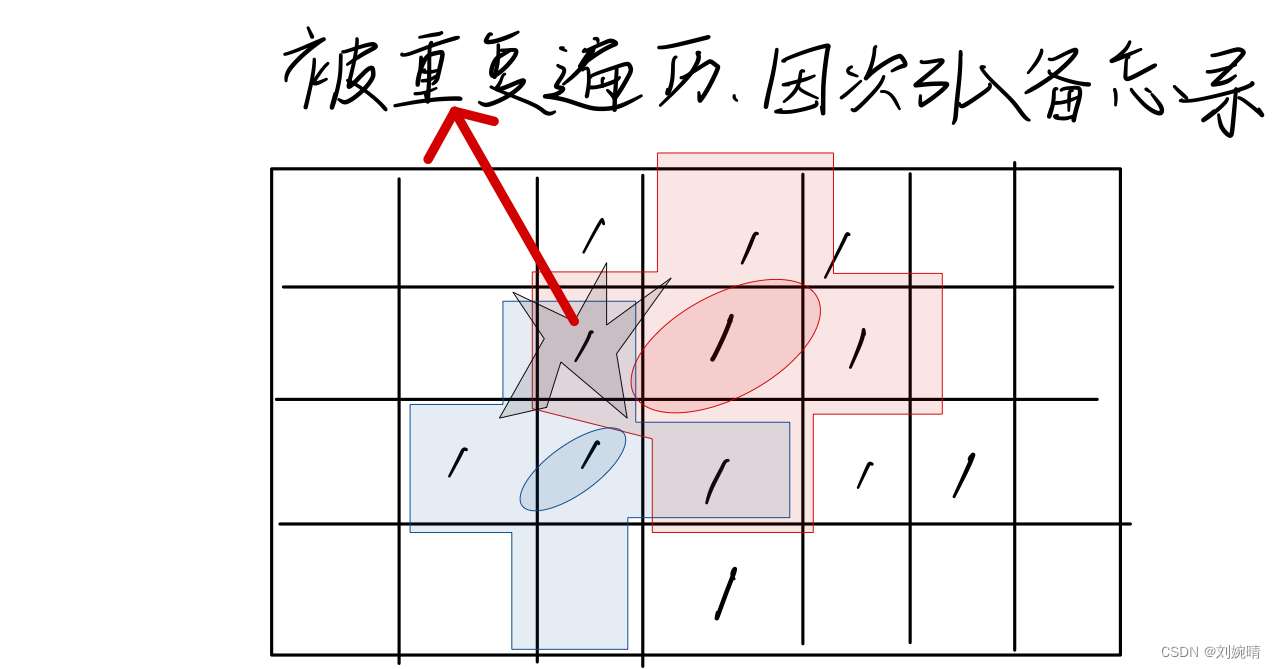
这里说明一下，岛屿问题中的备忘录问题，为什么在递归的过程中需要建立这样一个备忘录，我们可以看如下图解：

如果不建立备忘录，在递归过程中，可能会出现同一位置被多次递归调用的情况，这样增加了时间复杂度

备忘录实现方法 ： 本题的备忘录实现非常简单， 只需将已经遍历过的位置的值修改为2即可

例题一-岛屿的数量

题目描述： 求一个二维数组中存在的岛屿数量

对本题我们直接调用上述模板即可

class Solution {
    public int numIslands(char[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        int ans = 0;
        for(int i=0; i<m; i++){
            for(int j=0; j<n;j++){
                if(grid[i][j] == '1'){
                    // 递归过程中将属于同一岛屿的位置标记为2，保证属于同一岛屿的陆地1位置不会重复进入循环
                    dfs(grid, i, j);
                    ans++;
                }
            }
        }
        return ans;
    }
    public void dfs(char[][] grid, int m, int n){
        if(isBeyond(grid, m, n)){
            return;
        }
        if(grid[m][n] != '1'){
            return;
        }
        grid[m][n] = '2';
        dfs(grid, m-1, n);
        dfs(grid, m+1, n);
        dfs(grid, m, n-1);
        dfs(grid, m, n+1);
    }
    boolean isBeyond(char[][] grid, int m, int n){
        if(m < 0 || m>=grid.length || n<0 || n>=grid[0].length){
            return true;
        }
        return false;
    }
}

例题二-岛屿的周长

ps：输入保证只有一个岛屿

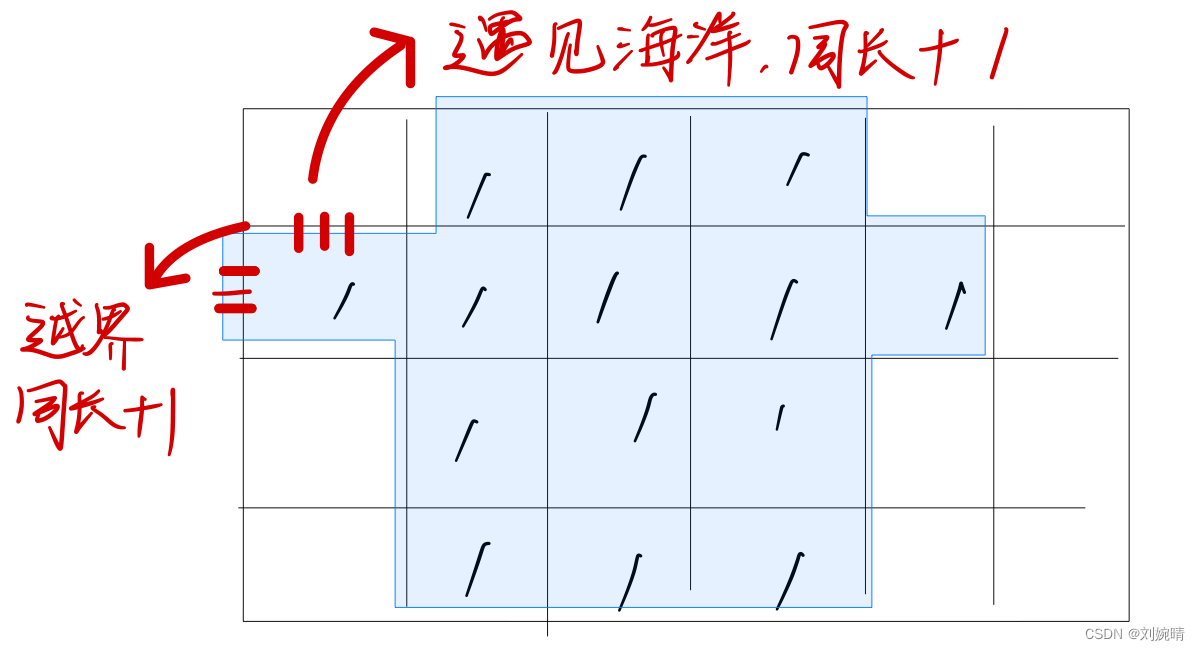
分析：

我们可以分析每一个陆地元素，对结果的贡献度，如下图解，经过分析可得，当陆地与海洋接壤一次或者越界一次对岛屿总周长的贡献度+1

代码

class Solution {
    // 从一个陆地方块走向一个非陆地方块，就将岛屿面积加1
    public int islandPerimeter(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        int perimeter = 0;
        for(int i=0; i<m; i++){
            for(int j=0; j<n; j++){
                if(grid[i][j] == 1){
                    // 因为只有一个岛屿，直接返回即可
                    return getPerimeter(grid, i, j);
                }
            }
        }
        return 0;
    }
    public int getPerimeter(int[][] grid, int m, int n){
        // 走到非陆地方块，返回共享度1
        if(isBeyond(grid, m, n) || grid[m][n] == 0){
            return 1;
        }
        // 走到遍历过方块返回0
        if(grid[m][n] == 2){
            return 0;
        }
        // 标记已经遍历过节点
        grid[m][n] = 2;
        return getPerimeter(grid, m-1, n)
        + getPerimeter(grid, m+1, n)
        + getPerimeter(grid, m, n-1)
        + getPerimeter(grid, m, n+1);
    }
    boolean isBeyond(int[][] grid, int m, int n){
        if(m < 0 || n < 0 || m >= grid.length || n >= grid[0].length){
            return true;
        }
        return false;
    }
}

到此这篇关于C++递归算法处理岛屿问题详解的文章就介绍到这了,更多相关C++岛屿问题内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！