Python绘制分形图案探索无限细节和奇妙之美

目录

• 一、目标
• 二、表示图像
• 三、画一条线
• 四、画三角形
• 五、生成分形
• 六、结论

分形是无限复杂的模式，在不同的尺度上具有自相似性。例如，一棵树的树干会分裂成更小的树枝。这些树枝又分裂成更小的树枝，以此类推。

通过编程的方式生成分形，可以将简单的形状变成复杂的重复图案。

本文将探讨如何利用一些简单的几何学基础和编程知识，在Python中建立令人印象深刻的分形图案。

分形在数据科学中发挥着重要作用。例如，在分形分析中，对数据集的分形特征进行评估，以帮助理解基础过程的结构。此外，处于分形生成中心的循环算法可以应用于广泛的数据问题，例如从二进制搜索算法到递归神经网络。

一、目标

写一个可以画等边三角形的程序，并且在三角形的每条边上，它必须能够绘制一个稍微小一点的向外的三角形。能够根据人的意愿多次重复此过程，从而创建一些有趣的模式。

二、表示图像

把图像表示为一个二维的像素阵列。像素阵列中的每个单元格将代表该像素的颜色（RGB）。

为此，可以使用NumPy库生成像素数组，并使用Pillow将其转换为可以保存的图像。

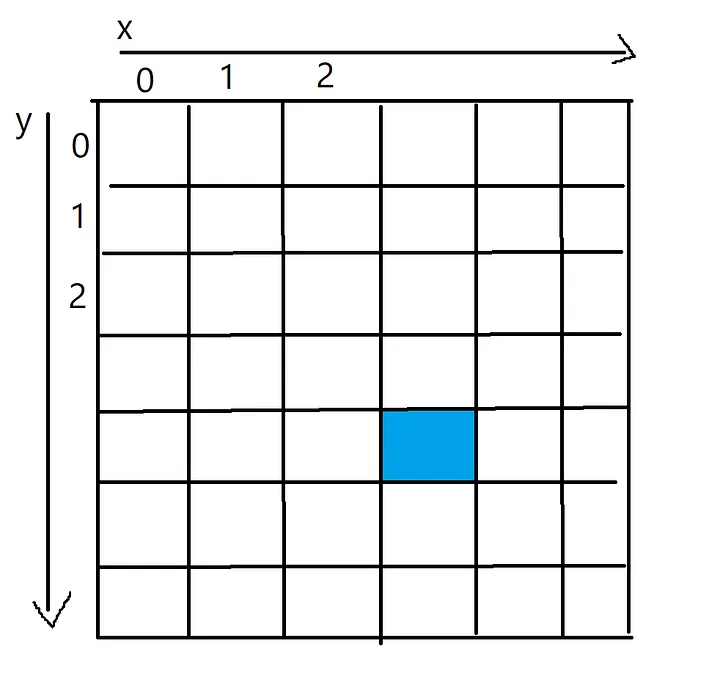
蓝色像素的x值为3，y值为4，可以通过一个二维数组访问，如pixels[4][3]

三、画一条线

现在开始编码，首先，需要一个可以获取两组坐标并在它们之间画一条线的函数。

下面的代码通过在两点之间插值来工作，每一步都向像素阵列添加新的像素。你可以把这个过程看作是在一条线上逐个像素地进行着色。

可以在每个代码片段中使用连续字符“\”来容纳一些较长的代码行。

import numpy as np
from PIL import Image
import math
def plot_line(from_coordinates, to_coordinates, thickness, colour, pixels):
    # 找出像素阵列的边界
    max_x_coordinate = len(pixels[0])
    max_y_coordinate = len(pixels)
    # 两点之间沿着x轴和y轴的距离
    horizontal_distance = to_coordinates[1] - from_coordinates[1]
    vertical_distance = to_coordinates[0] - from_coordinates[0]
    # 两点之间的总距离
    distance =  math.sqrt((to_coordinates[1] - from_coordinates[1])**2 \
                + (to_coordinates[0] - from_coordinates[0])**2)
    # 每次给一个新的像素上色时，将向前走多远
    horizontal_step = horizontal_distance/distance
    vertical_step = vertical_distance/distance
    # 此时，将进入循环以在像素数组中绘制线
    # 循环的每一次迭代都会沿着线添加一个新的点
    for i in range(round(distance)):
        # 这两个坐标是直线中心的坐标
        current_x_coordinate = round(from_coordinates[1] + (horizontal_step*i))
        current_y_coordinate = round(from_coordinates[0] + (vertical_step*i))
        # 一旦得到了点的坐标，
        # 就在坐标周围画出尺寸为thickness的图案
        for x in range (-thickness, thickness):
            for y in range (-thickness, thickness):
                x_value = current_x_coordinate + x
                y_value = current_y_coordinate + y
                if (x_value > 0 and x_value < max_x_coordinate and \
                    y_value > 0 and y_value < max_y_coordinate):
                    pixels[y_value][x_value] = colour
# 定义图像的大小
pixels = np.zeros( (500,500,3), dtype=np.uint8 )
# 画一条线
plot_line([0,0], [499,499], 1, [255,200,0], pixels)
# 把像素阵列变成一张真正的图片
img = Image.fromarray(pixels)
# 显示得到的图片，并保存它
img.show()
img.save('Line.png')

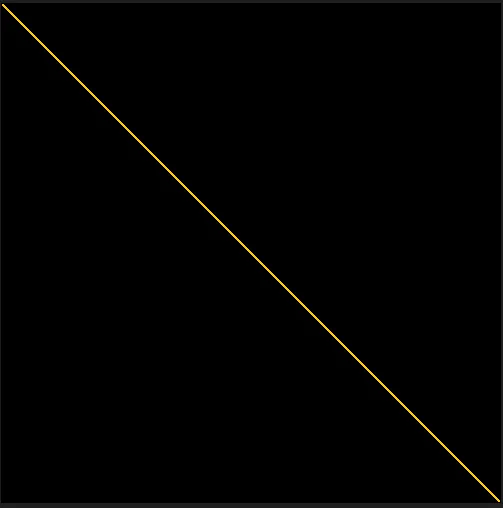
此函数在像素阵列的每个角之间绘制一条黄线时的结果

四、画三角形

现在有了一个可以在两点之间画线的函数，可以画第一个等边三角形了。

给定三角形的中心点和边长，可以使用公式计算出高度：h = ½(√3a)。

现在利用这个高度、中心点和边长，可以计算出三角形的每个角的位置。使用之前制作的plot_line函数，可以在每个角之间画一条线。

def draw_triangle(center, side_length, thickness, colour, pixels):
    # 等边三角形的高度是，h = ½(√3a)
    # 其中a是边长
    triangle_height = round(side_length * math.sqrt(3)/2)
    # 顶角
    top = [center[0] - triangle_height/2, center[1]]
    # 左下角
    bottom_left = [center[0] + triangle_height/2, center[1] - side_length/2]
    # 右下角
    bottom_right = [center[0] + triangle_height/2, center[1] + side_length/2]
    # 在每个角之间画一条线来完成三角形
    plot_line(top, bottom_left, thickness, colour, pixels)
    plot_line(top, bottom_right, thickness, colour, pixels)
    plot_line(bottom_left, bottom_right, thickness, colour, pixels)

在500x500像素PNG的中心绘制三角形时的结果

五、生成分形

一切都已准备就绪，可以用Python创建第一个分形。

但是最后一步是最难完成的，三角形函数为它的每一边调用自己，需要能够计算每个新的较小三角形的中心点，并正确地旋转它们，使它们垂直于它们所附着的一侧。

通过从旋转的坐标中减去中心点的偏移量，然后应用公式来旋转一对坐标，可以用这个函数来旋转三角形的每个角。

def rotate(coordinate, center_point, degrees):
    # 从坐标中减去旋转的点
    x = (coordinate[0] - center_point[0])
    y = (coordinate[1] - center_point[1])
    # Python的cos和sin函数采用弧度而不是度数
    radians = math.radians(degrees)
    # 计算旋转点
    new_x = (x * math.cos(radians)) - (y * math.sin(radians))
    new_y = (y * math.cos(radians)) + (x * math.sin(radians))
    # 将在开始时减去的偏移量加回旋转点上
    return [new_x + center_point[0], new_y + center_point[1]]

将每个坐标旋转35度的三角形

可以旋转一个三角形后，思考如何在第一个三角形的每条边上画一个新的小三角形。

为了实现这一点，扩展draw_triangle函数，为每条边计算一个新三角形的旋转和中心点，其边长被参数shrink_side_by减少。

一旦它计算出新三角形的中心点和旋转，它就会调用draw_triangle（自身）来从当前线的中心画出新的、更小的三角形。然后，这将反过来打击同一个代码块，为一个更小的三角形计算另一组中心点和旋转。

这就是所谓的循环算法，因为draw_triangle函数现在会调用自己，直到达到希望绘制的三角形的最大深度。有这个转义句子是很重要的，因为理论上这个函数会一直循环下去（但实际上调用堆栈会变得太大，导致堆栈溢出错误）。

def draw_triangle(center, side_length, degrees_rotate, thickness, colour, \
                  pixels, shrink_side_by, iteration, max_depth):
    # 等边三角形的高度是，h = ½(√3a)
    # 其中'a'是边长
    triangle_height = side_length * math.sqrt(3)/2
    # 顶角
    top = [center[0] - triangle_height/2, center[1]]
    # 左下角
    bottom_left = [center[0] + triangle_height/2, center[1] - side_length/2]
    # 右下角
    bottom_right = [center[0] + triangle_height/2, center[1] + side_length/2]
    if (degrees_rotate != 0):
        top = rotate(top, center, degrees_rotate)
        bottom_left = rotate(bottom_left, center, degrees_rotate)
        bottom_right = rotate(bottom_right, center, degrees_rotate)
    # 三角形各边之间的坐标
    lines = [[top, bottom_left],[top, bottom_right],[bottom_left, bottom_right]]
    line_number = 0
    # 在每个角之间画一条线来完成三角形
    for line in lines:
        line_number += 1
        plot_line(line[0], line[1], thickness, colour, pixels)
        # 如果还没有达到max_depth，就画一些新的三角形
        if (iteration < max_depth and (iteration < 1 or line_number < 3)):
            gradient = (line[1][0] - line[0][0]) / (line[1][1] - line[0][1])
            new_side_length = side_length*shrink_side_by
            # 正在绘制的三角形线的中心
            center_of_line = [(line[0][0] + line[1][0]) / 2, \
                              (line[0][1] + line[1][1]) / 2]
            new_center = []
            new_rotation = degrees_rotate
            # 需要旋转traingle的数量
            if (line_number == 1):
                new_rotation += 60
            elif (line_number == 2):
                new_rotation -= 60
            else:
                new_rotation += 180
            # 在一个理想的世界里，这将是gradient=0，
            # 但由于浮点除法的原因，无法
            # 确保永远是这种情况
            if (gradient < 0.0001 and gradient > -0.0001):
                if (center_of_line[0] - center[0] > 0):
                    new_center = [center_of_line[0] + triangle_height * \
                                 (shrink_side_by/2), center_of_line[1]]
                else:
                    new_center = [center_of_line[0] - triangle_height * \
                                  (shrink_side_by/2), center_of_line[1]]
            else:
                # 计算直线梯度的法线
                difference_from_center = -1/gradient
                # 计算这条线距中心的距离
                # 到新三角形的中心
                distance_from_center = triangle_height * (shrink_side_by/2)
                # 计算 x 方向的长度，
                # 从线的中心到新三角形的中心
                x_length = math.sqrt((distance_from_center**2)/ \
                                     (1 + difference_from_center**2))
                # 计算出x方向需要走哪条路
                if (center_of_line[1] < center[1] and x_length > 0):
                    x_length *= -1
                # 现在计算Y方向的长度
                y_length = x_length * difference_from_center
                # 用新的x和y值来偏移线的中心
                new_center = [center_of_line[0] + y_length, \
                              center_of_line[1] + x_length]
            draw_triangle(new_center, new_side_length, new_rotation, \
                          thickness, colour, pixels, shrink_side_by, \
                          iteration+1, max_depth)

三角形分形，收缩边=1/2，最大深度=2

六、结论

下面是通过修改输入到draw_triangle函数的shrink_side_by和max_depth值生成的不同图像的一些示例。

有趣的是，这些多次重复的图案往往能创造出更复杂的形状，比如六边形，但却具有令人着迷的对称性。

越来越复杂的形状开始在重复三角形的对称性中出现

另一个分形，每次迭代使用较小的尺寸减小

分形是非常有趣的玩法，可以创造出美丽的图案。使用一些简单的概念和丰富的创造力，可以产生非常令人印象深刻的结构。

在理解分形的核心属性和应用循环算法的过程中打下的坚实基础，可以帮助理解数据科学中更复杂的分形问题。

到此这篇关于Python绘制分形图案探索无限细节和奇妙之美的文章就介绍到这了,更多相关Python绘制分形图案内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！