Python数据可视化实现正态分布（高斯分布）

正态分布（Normal distribution）又成为高斯分布（Gaussian distribution）

若随机变量X服从一个数学期望为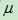、标准方差为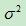的高斯分布，记为：

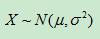
则其概率密度函数为：

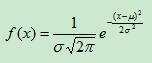
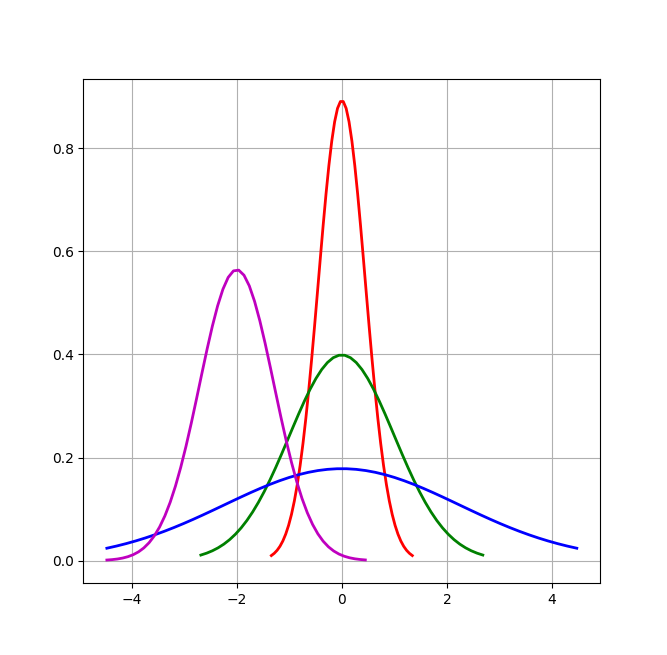
正态分布的期望值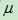决定了其位置，其标准差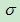决定了分布的幅度。因其曲线呈钟形，因此人们又经常称之为钟形曲线。我们通常所说的标准正态分布是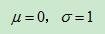的正态分布：

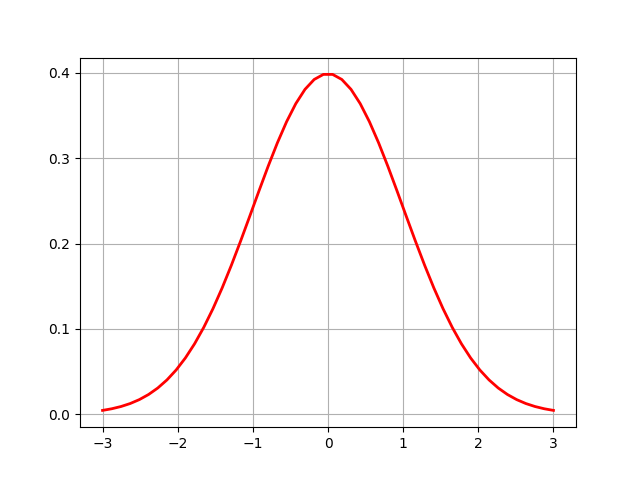
概率密度函数

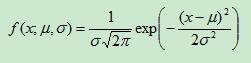
代码实现：

# Python实现正态分布
  # 绘制正态分布概率密度函数
  u = 0  # 均值μ
  u01 = -2
  sig = math.sqrt(0.2) # 标准差δ
  sig01 = math.sqrt(1)
  sig02 = math.sqrt(5)
  sig_u01 = math.sqrt(0.5)
  x = np.linspace(u - 3*sig, u + 3*sig, 50)
  x_01 = np.linspace(u - 6 * sig, u + 6 * sig, 50)
  x_02 = np.linspace(u - 10 * sig, u + 10 * sig, 50)
  x_u01 = np.linspace(u - 10 * sig, u + 1 * sig, 50)
  y_sig = np.exp(-(x - u) ** 2 /(2* sig **2))/(math.sqrt(2*math.pi)*sig)
  y_sig01 = np.exp(-(x_01 - u) ** 2 /(2* sig01 **2))/(math.sqrt(2*math.pi)*sig01)
  y_sig02 = np.exp(-(x_02 - u) ** 2 / (2 * sig02 ** 2)) / (math.sqrt(2 * math.pi) * sig02)
  y_sig_u01 = np.exp(-(x_u01 - u01) ** 2 / (2 * sig_u01 ** 2)) / (math.sqrt(2 * math.pi) * sig_u01)
  plt.plot(x, y_sig, "r-", linewidth=2)
  plt.plot(x_01, y_sig01, "g-", linewidth=2)
  plt.plot(x_02, y_sig02, "b-", linewidth=2)
  plt.plot(x_u01, y_sig_u01, "m-", linewidth=2)
  # plt.plot(x, y, 'r-', x, y, 'go', linewidth=2,markersize=8)
  plt.grid(True)
  plt.show()

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。

赞 (0)

相关推荐

  • Python数据可视化正态分布简单分析及实现代码

    Python数据可视化正态分布简单分析及实现代码

    Python说来简单也简单,但是也不简单,尤其是再跟高数结合起来的时候... 正态分布(Normaldistribution),也称"常态分布",又名高斯分布(Gaussiandistribution),最早由A.棣莫弗在求二项分布的渐近公式中得到.C.F.高斯在研究测量误差时从另一个角度导出了它.P.S.拉普拉斯和高斯研究了它的性质.是一个在数学.物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力. 正态曲线呈钟型,两头低,中间高,左右对称因其曲线呈钟形,因此人

  • 使用python绘制3维正态分布图的方法

    今天使用python画了几个好玩的3D展示图,现在分享给大家. 先贴上图片 使用的python工具包为: from matplotlib import pyplot as plt import numpy as np from mpl_toolkits.mplot3d import Axes3D 在贴代码之前,有必要从整体上了解这些图是如何画出来的.可以把上面每一个3D图片理解成一个长方体.输入数据是三维的,x轴y轴和z轴.在第三个图片里面有x.y和z坐标的标识.在第三张图片中,我们可以理解为,

  • Python使用numpy产生正态分布随机数的向量或矩阵操作示例

    Python使用numpy产生正态分布随机数的向量或矩阵操作示例

    本文实例讲述了Python使用numpy产生正态分布随机数的向量或矩阵操作.分享给大家供大家参考,具体如下: 简单来说,正态分布(Normal distribution)又名高斯分布(Gaussian distribution),是一个在数学.物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力.一般的正态分布可以通过标准正态分布配合数学期望向量和协方差矩阵得到.如下代码,可以得到满足一维和二维正态分布的样本. 示例1(一维正态分布): # coding=utf-8 '''

  • 在python中画正态分布图像的实例

    1.正态分布简介 正态分布(normal distribtution)又叫做高斯分布(Gaussian distribution),是一个非常重要也非常常见的连续概率分布.正态分布大家也都非常熟悉,下面做一些简单的介绍. 假设随机变量XX服从一个位置参数为μμ.尺度参数为σσ的正态分布,则可以记为: 而概率密度函数为 2.在python中画正态分布直方图 先直接上代码 import numpy as np import matplotlib.mlab as mlab import matplot

  • Python数据可视化实现正态分布（高斯分布）

    正态分布(Normal distribution)又成为高斯分布(Gaussian distribution) 若随机变量X服从一个数学期望为.标准方差为的高斯分布,记为: 则其概率密度函数为: 正态分布的期望值决定了其位置,其标准差决定了分布的幅度.因其曲线呈钟形,因此人们又经常称之为钟形曲线.我们通常所说的标准正态分布是的正态分布: 概率密度函数 代码实现: # Python实现正态分布 # 绘制正态分布概率密度函数 u = 0 # 均值μ u01 = -2 sig = math.sqrt(

  • Python数据可视化:幂律分布实例详解

    1.公式推导 对幂律分布公式: 对公式两边同时取以10为底的对数: 所以对于幂律公式,对X,Y取对数后,在坐标轴上为线性方程. 2.可视化 从图形上来说,幂律分布及其拟合效果: 对X轴与Y轴取以10为底的对数.效果上就是X轴上1与10,与10与100的距离是一样的. 对XY取双对数后,坐标轴上点可以很好用直线拟合.所以,判定数据是否符合幂律分布,只需要对XY取双对数,判断能否用一个直线很好拟合就行.常见的直线拟合效果评估标准有拟合误差平方和.R平方. 3.代码实现 #!/usr/bin/env

  • python数据可视化使用pyfinance分析证券收益示例详解

    python数据可视化使用pyfinance分析证券收益示例详解

    目录 pyfinance简介 pyfinance包含六个模块 returns模块应用实例 收益率计算 CAPM模型相关指标 风险指标 基准比较指标 风险调整收益指标 综合业绩评价指标分析实例 结语 pyfinance简介 在查找如何使用Python实现滚动回归时,发现一个很有用的量化金融包--pyfinance.顾名思义,pyfinance是为投资管理和证券收益分析而构建的Python分析包,主要是对面向定量金融的现有包进行补充,如pyfolio和pandas等. pyfinance包含六个模块

  • Python数据可视化之Seaborn的使用详解

    Python数据可视化之Seaborn的使用详解

    目录 1. 安装 seaborn 2.准备数据 3.背景与边框 3.1 设置背景风格 3.2 其他 3.3 边框控制 4. 绘制 散点图 5. 绘制 折线图 5.1 使用 replot()方法 5.2 使用 lineplot()方法 6. 绘制直方图 displot() 7. 绘制条形图 barplot() 8. 绘制线性回归模型 9. 绘制 核密度图 kdeplot() 9.1 一般核密度图 9.2 边际核密度图 10. 绘制 箱线图 boxplot() 11. 绘制 提琴图 violinpl

  • 基于Python数据可视化利器Matplotlib,绘图入门篇,Pyplot详解

    基于Python数据可视化利器Matplotlib,绘图入门篇,Pyplot详解

    Pyplot matplotlib.pyplot是一个命令型函数集合,它可以让我们像使用MATLAB一样使用matplotlib.pyplot中的每一个函数都会对画布图像作出相应的改变,如创建画布.在画布中创建一个绘图区.在绘图区上画几条线.给图像添加文字说明等.下面我们就通过实例代码来领略一下他的魅力. import matplotlib.pyplot as plt plt.plot([1,2,3,4]) plt.ylabel('some numbers') plt.show() 上图是我们通

  • 详解Python数据可视化编程 - 词云生成并保存（jieba+WordCloud）

    详解Python数据可视化编程 - 词云生成并保存（jieba+WordCloud）

    思维导图: 效果(语句版): 源码: # -*- coding: utf-8 -*- """ Created on Tue Mar 5 17:59:29 2019 @author: dell """ # ============================================================================= # 步骤: # 分割aaa = jieba.cut(str,cut_all=True/Fa

  • Python数据可视化:顶级绘图库plotly详解

    有史以来最牛逼的绘图工具,没有之一 plotly是现代平台的敏捷商业智能和数据科学库,它作为一款开源的绘图库,可以应用于Python.R.MATLAB.Excel.JavaScript和jupyter等多种语言,主要使用的js进行图形绘制,实现过程中主要就是调用plotly的函数接口,底层实现完全被隐藏,便于初学者的掌握. 下面主要从Python的角度来分析plotly的绘图原理及方法: ###安装plotly: 使用pip来安装plotly库,如果机器上没有pip,需要先进行pip的安装,这里

  • Python数据可视化:饼状图的实例讲解

    使用python实现论文里面的饼状图: 原图: python代码实现: # # 饼状图 # plot.figure(figsize=(8,8)) labels = [u'Canteen', u'Supermarket', u'Dorm', u'Others'] sizes = [73, 21, 4, 2] colors = ['red', 'yellow', 'blue', 'green'] explode = (0.05, 0, 0, 0) patches, l_text, p_text =

  • Python数据可视化:泊松分布详解

    一个服从泊松分布的随机变量X,表示在具有比率参数(rate parameter)λ的一段固定时间间隔内,事件发生的次数.参数λ告诉你该事件发生的比率.随机变量X的平均值和方差都是λ. 代码实现: # Poisson分布 x = np.random.poisson(lam=5, size=10000) # lam为λ size为k pillar = 15 a = plt.hist(x, bins=pillar, normed=True, range=[0, pillar], color='g',

随机推荐