javascript trie前缀树的示例

引子

Trie树（来自单词retrieval），又称前缀字，单词查找树，字典树，是一种树形结构，是一种哈希树的变种，是一种用于快速检索的多叉树结构。

它的优点是：最大限度地减少无谓的字符串比较，查询效率比哈希表高。

Trie的核心思想是空间换时间。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。

Trie树也有它的缺点, 假定我们只对字母与数字进行处理，那么每个节点至少有52＋10个子节点。为了节省内存，我们可以用链表或数组。在JS中我们直接用数组，因为JS的数组是动态的，自带优化。

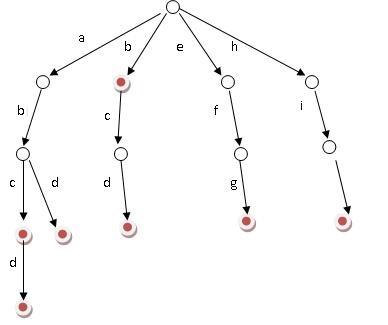
基本性质

1. 根节点不包含字符，除根节点外的每一个子节点都包含一个字符
2. 从根节点到某一节点。路径上经过的字符连接起来，就是该节点对应的字符串
3. 每个节点的所有子节点包含的字符都不相同

程序实现

// by 司徒正美
class Trie {
 constructor() {
  this.root = new TrieNode();
 }
 isValid(str) {
  return /^[a-z1-9]+$/i.test(str);
 }
 insert(word) {
  // addWord
  if (this.isValid(word)) {
   var cur = this.root;
   for (var i = 0; i < word.length; i++) {
    var c = word.charCodeAt(i);
    c -= 48; //减少”0“的charCode
    var node = cur.son[c];
    if (node == null) {
     var node = (cur.son[c] = new TrieNode());
     node.value = word.charAt(i);
     node.numPass = 1; //有N个字符串经过它
    } else {
     node.numPass++;
    }
    cur = node;
   }
   cur.isEnd = true; //樯记有字符串到此节点已经结束
   cur.numEnd++; //这个字符串重复次数

   return true;
  } else {
   return false;
  }
 }
 remove(word){
   if (this.isValid(word)) {
     var cur = this.root;
     var array = [], n = word.length
     for (var i = 0; i < n; i++) {
       var c = word.charCodeAt(i);
       c = this.getIndex(c)
       var node = cur.son[c];
       if(node){
         array.push(node)
         cur = node
       }else{
         return false
       }

     }
     if(array.length === n){
       array.forEach(function(){
         el.numPass--
       })
       cur.numEnd --
       if( cur.numEnd == 0){
         cur.isEnd = false
       }
     }
   }else{
     return false
   }
 }
 preTraversal(cb){//先序遍历
    function preTraversalImpl(root, str, cb){
      cb(root, str);
      for(let i = 0,n = root.son.length; i < n; i ++){
        let node = root.son[i];
        if(node){
          preTraversalImpl(node, str + node.value, cb);
        }
      }
    }
    preTraversalImpl(this.root, "", cb);
  }
 // 在字典树中查找是否存在某字符串为前缀开头的字符串(包括前缀字符串本身)
 isContainPrefix(word) {
  if (this.isValid(word)) {
   var cur = this.root;
   for (var i = 0; i < word.length; i++) {
    var c = word.charCodeAt(i);
    c -= 48; //减少”0“的charCode
    if (cur.son[c]) {
     cur = cur.son[c];
    } else {
     return false;
    }
   }
   return true;
  } else {
   return false;
  }
 }
 isContainWord(str) {
  // 在字典树中查找是否存在某字符串(不为前缀)
  if (this.isValid(word)) {
   var cur = this.root;
   for (var i = 0; i < word.length; i++) {
    var c = word.charCodeAt(i);
    c -= 48; //减少”0“的charCode
    if (cur.son[c]) {
     cur = cur.son[c];
    } else {
     return false;
    }
   }
   return cur.isEnd;
  } else {
   return false;
  }
 }
 countPrefix(word) {
  // 统计以指定字符串为前缀的字符串数量
  if (this.isValid(word)) {
   var cur = this.root;
   for (var i = 0; i < word.length; i++) {
    var c = word.charCodeAt(i);
    c -= 48; //减少”0“的charCode
    if (cur.son[c]) {
     cur = cur.son[c];
    } else {
     return 0;
    }
   }
   return cur.numPass;
  } else {
   return 0;
  }
 }
 countWord(word) {
  // 统计某字符串出现的次数方法
  if (this.isValid(word)) {
   var cur = this.root;
   for (var i = 0; i < word.length; i++) {
    var c = word.charCodeAt(i);
    c -= 48; //减少”0“的charCode
    if (cur.son[c]) {
     cur = cur.son[c];
    } else {
     return 0;
    }
   }
   return cur.numEnd;
  } else {
   return 0;
  }
 }
}

class TrieNode {
 constructor() {
  this.numPass = 0;//有多少个单词经过这节点
  this.numEnd = 0; //有多少个单词就此结束
  this.son = [];
  this.value = ""; //value为单个字符
  this.isEnd = false;
 }
}

我们重点看一下TrieNode与Trie的insert方法。 由于字典树是主要用在词频统计，因此它的节点属性比较多, 包含了numPass, numEnd但非常重要的属性。

insert方法是用于插入重词，在开始之前，我们必须判定单词是否合法，不能出现 特殊字符与空白。在插入时是打散了一个个字符放入每个节点中。每经过一个节点都要修改numPass。

优化

现在我们每个方法中，都有一个c=-48的操作，其实数字与大写字母与小写字母间其实还有其他字符的，这样会造成无谓的空间的浪费

// by 司徒正美
getIndex(c){
   if(c < 58){//48-57
     return c - 48
   }else if(c < 91){//65-90
     return c - 65 + 11
   }else {//> 97
     return c - 97 + 26+ 11
   }
 }

然后相关方法将c-= 48改成c = this.getIndex(c)即可

测试

var trie = new Trie();
  trie.insert("I");
  trie.insert("Love");
  trie.insert("China");
  trie.insert("China");
  trie.insert("China");
  trie.insert("China");
  trie.insert("China");
  trie.insert("xiaoliang");
  trie.insert("xiaoliang");
  trie.insert("man");
  trie.insert("handsome");
  trie.insert("love");
  trie.insert("Chinaha");
  trie.insert("her");
  trie.insert("know");
  var map = {}
  trie.preTraversal(function(node, str){
    if(node.isEnd){
     map[str] = node.numEnd
    }
  })
  for(var i in map){
    console.log(i+" 出现了"+ map[i]+" 次")
  }
  console.log("包含Chin（包括本身）前缀的单词及出现次数：");
  //console.log("China")
  var map = {}
  trie.preTraversal(function(node, str){
    if(str.indexOf("Chin") === 0 && node.isEnd){
      map[str] = node.numEnd
    }
   })
  for(var i in map){
    console.log(i+" 出现了"+ map[i]+" 次")
  }

Trie树和其它数据结构的比较

Trie树与二叉搜索树

二叉搜索树应该是我们最早接触的树结构了，我们知道，数据规模为n时，二叉搜索树插入、查找、删除操作的时间复杂度通常只有O(log n)，最坏情况下整棵树所有的节点都只有一个子节点，退变成一个线性表，此时插入、查找、删除操作的时间复杂度是O(n)。

通常情况下，Trie树的高度n要远大于搜索字符串的长度m，故查找操作的时间复杂度通常为O(m)，最坏情况下的时间复杂度才为O(n)。很容易看出，Trie树最坏情况下的查找也快过二叉搜索树。

文中Trie树都是拿字符串举例的，其实它本身对key的适宜性是有严格要求的，如果key是浮点数的话，就可能导致整个Trie树巨长无比，节点可读性也非常差，这种情况下是不适宜用Trie树来保存数据的；而二叉搜索树就不存在这个问题。

Trie树与Hash表

考虑一下Hash冲突的问题。Hash表通常我们说它的复杂度是O(1)，其实严格说起来这是接近完美的Hash表的复杂度，另外还需要考虑到hash函数本身需要遍历搜索字符串，复杂度是O(m)。在不同键被映射到“同一个位置”（考虑closed hashing，这“同一个位置”可以由一个普通链表来取代）的时候，需要进行查找的复杂度取决于这“同一个位置”下节点的数目，因此，在最坏情况下，Hash表也是可以成为一张单向链表的。

Trie树可以比较方便地按照key的字母序来排序（整棵树先序遍历一次就好了），这跟绝大多数Hash表是不同的（Hash表一般对于不同的key来说是无序的）。

在较理想的情况下，Hash表可以以O(1)的速度迅速命中目标，如果这张表非常大，需要放到磁盘上的话，Hash表的查找访问在理想情况下只需要一次即可；但是Trie树访问磁盘的数目需要等于节点深度。

很多时候Trie树比Hash表需要更多的空间，我们考虑这种一个节点存放一个字符的情况的话，在保存一个字符串的时候，没有办法把它保存成一个单独的块。Trie树的节点压缩可以明显缓解这个问题，后面会讲到。

Trie树的改进

按位Trie树（Bitwise Trie）

原理上和普通Trie树差不多，只不过普通Trie树存储的最小单位是字符，但是Bitwise Trie存放的是位而已。位数据的存取由CPU指令一次直接实现，对于二进制数据，它理论上要比普通Trie树快。

节点压缩。

分支压缩：对于稳定的Trie树，基本上都是查找和读取操作，完全可以把一些分支进行压缩。例如，前图中最右侧分支的inn可以直接压缩成一个节点“inn”，而不需要作为一棵常规的子树存在。Radix树就是根据这个原理来解决Trie树过深问题的。

节点映射表：这种方式也是在Trie树的节点可能已经几乎完全确定的情况下采用的，针对Trie树中节点的每一个状态，如果状态总数重复很多的话，通过一个元素为数字的多维数组（比如Triple Array Trie）来表示，这样存储Trie树本身的空间开销会小一些，虽说引入了一张额外的映射表。

前缀树的应用

前缀树还是很好理解，它的应用也是非常广的。

（1）字符串的快速检索

字典树的查询时间复杂度是O(logL)，L是字符串的长度。所以效率还是比较高的。字典树的效率比hash表高。

（2）字符串排序

从上图我们很容易看出单词是排序的，先遍历字母序在前面。减少了没必要的公共子串。

（3）最长公共前缀

inn和int的最长公共前缀是in，遍历字典树到字母n时，此时这些单词的公共前缀是in。

（4）自动匹配前缀显示后缀

我们使用辞典或者是搜索引擎的时候，输入appl，后面会自动显示一堆前缀是appl的东东吧。那么有可能是通过字典树实现的，前面也说了字典树可以找到公共前缀，我们只需要把剩余的后缀遍历显示出来即可。

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。

您可能感兴趣的文章:

• JavaScript实现二叉树定义、遍历及查找的方法详解
• JS实现二叉查找树的建立以及一些遍历方法实现
• JavaScript数据结构之二叉树的查找算法示例
• JavaScript数据结构之二叉查找树的定义与表示方法