详解如何用c++实现平衡二叉树

一、概述

平衡二叉树具有以下性质：它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。这个方案很好的解决了二叉查找树退化成链表的问题，把插入，查找，删除的时间复杂度最好情况和最坏情况都维持在O(logN)。但是频繁旋转会使插入和删除牺牲掉O(logN)左右的时间，不过相对二叉查找树来说，时间上稳定了很多。

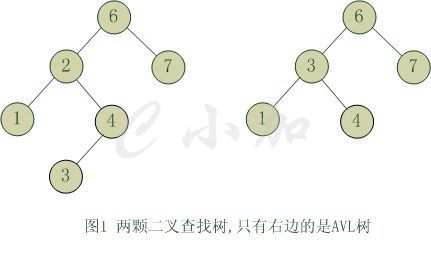
平衡二叉树大部分操作和二叉查找树类似，主要不同在于插入删除的时候平衡二叉树的平衡可能被改变，并且只有从那些插入点到根结点的路径上的结点的平衡性可能被改变，因为只有这些结点的子树可能变化。

二、平衡二叉树不平衡的情形

把需要重新平衡的结点叫做α，由于任意两个结点最多只有两个儿子，因此高度不平衡时，α结点的两颗子树的高度相差2.容易看出，这种不平衡可能出现在下面4中情况中：

1.对α的左儿子的左子树进行一次插入

2.对α的左儿子的右子树进行一次插入

3.对α的右儿子的左子树进行一次插入

4.对α的右儿子的右子树进行一次插入

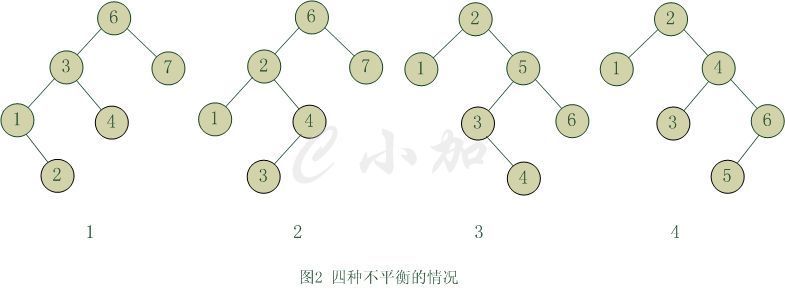
情形1和情形4是关于α的镜像对称，二情形2和情形3也是关于α的镜像对称，因此理论上看只有两种情况，但编程的角度看还是四种情形。

第一种情况是插入发生在“外边”的情形（左左或右右），该情况可以通过一次单旋转完成调整；第二种情况是插入发生在“内部”的情形（左右或右左），这种情况比较复杂，需要通过双旋转来调整。

三、调整措施

3.1、单旋转

上图是左左的情况，k2结点不满足平衡性，它的左子树k1比右子树z深两层，k1子树中更深的是k1的左子树x，因此属于左左情况。

为了恢复平衡，我们把x上移一层，并把z下移一层，但此时实际已经超出了AVL树的性质要求。为此，重新安排结点以形成一颗等价的树。为使树恢复平衡，我们把k2变成这棵树的根节点，因为k2大于k1，把k2置于k1的右子树上，而原本在k1右子树的Y大于k1，小于k2，就把Y置于k2的左子树上，这样既满足了二叉查找树的性质，又满足了平衡二叉树的性质。

这种情况称为单旋转。

3.2、双旋转

对于左右和右左两种情况，单旋转不能解决问题，要经过两次旋转。

对于上图情况，为使树恢复平衡，我们需要进行两步，第一步，把k1作为根，进行一次右右旋转，旋转之后就变成了左左情况，所以第二步再进行一次左左旋转，最后得到了一棵以k2为根的平衡二叉树。

四、AVL树的删除操作

同插入操作一样，删除结点时也有可能破坏平衡性，这就要求我们删除的时候要进行平衡性调整。

删除分为以下几种情况：

首先在整个二叉树中搜索要删除的结点，如果没搜索到直接返回不作处理，否则执行以下操作：

1.要删除的节点是当前根节点T。

如果左右子树都非空。在高度较大的子树中实施删除操作。

分两种情况：

(1)、左子树高度大于右子树高度，将左子树中最大的那个元素赋给当前根节点，然后删除左子树中元素值最大的那个节点。

(1)、左子树高度小于右子树高度，将右子树中最小的那个元素赋给当前根节点，然后删除右子树中元素值最小的那个节点。

如果左右子树中有一个为空，那么直接用那个非空子树或者是NULL替换当前根节点即可。

2、要删除的节点元素值小于当前根节点T值，在左子树中进行删除。

递归调用，在左子树中实施删除。

这个是需要判断当前根节点是否仍然满足平衡条件，

如果满足平衡条件，只需要更新当前根节点T的高度信息。

否则，需要进行旋转调整：

如果T的左子节点的左子树的高度大于T的左子节点的右子树的高度，进行相应的单旋转。否则进行双旋转。

3、要删除的节点元素值大于当前根节点T值，在右子树中进行删除。

五、代码实现

AvlTree.h

#include <iostream>
#include <algorithm>
using namespace std;
#pragma once

//平衡二叉树结点
template <typename T>
struct AvlNode
{
    T data;
    int height; //结点所在高度
    AvlNode<T> *left;
    AvlNode<T> *right;
    AvlNode<T>(const T theData) : data(theData), left(NULL), right(NULL), height(0){}
};

//AvlTree
template <typename T>
class AvlTree
{
public:
    AvlTree<T>(){}
    ~AvlTree<T>(){}
    AvlNode<T> *root;
    //插入结点
    void Insert(AvlNode<T> *&t, T x);
    //删除结点
    bool Delete(AvlNode<T> *&t, T x);
    //查找是否存在给定值的结点
    bool Contains(AvlNode<T> *t, const T x) const;
    //中序遍历
    void InorderTraversal(AvlNode<T> *t);
    //前序遍历
    void PreorderTraversal(AvlNode<T> *t);
    //最小值结点
    AvlNode<T> *FindMin(AvlNode<T> *t) const;
    //最大值结点
    AvlNode<T> *FindMax(AvlNode<T> *t) const;
private:
    //求树的高度
    int GetHeight(AvlNode<T> *t);
    //单旋转 左
    AvlNode<T> *LL(AvlNode<T> *t);
    //单旋转 右
    AvlNode<T> *RR(AvlNode<T> *t);
    //双旋转 右左
    AvlNode<T> *LR(AvlNode<T> *t);
    //双旋转 左右
    AvlNode<T> *RL(AvlNode<T> *t);
};

template <typename T>
AvlNode<T> * AvlTree<T>::FindMax(AvlNode<T> *t) const
{
    if (t == NULL)
        return NULL;
    if (t->right == NULL)
        return t;
    return FindMax(t->right);
}

template <typename T>
AvlNode<T> * AvlTree<T>::FindMin(AvlNode<T> *t) const
{
    if (t == NULL)
        return NULL;
    if (t->left == NULL)
        return t;
    return FindMin(t->left);
}

template <typename T>
int AvlTree<T>::GetHeight(AvlNode<T> *t)
{
    if (t == NULL)
        return -1;
    else
        return t->height;
}

//单旋转
//左左插入导致的不平衡
template <typename T>
AvlNode<T> * AvlTree<T>::LL(AvlNode<T> *t)
{
    AvlNode<T> *q = t->left;
    t->left = q->right;
    q->right = t;
    t = q;
    t->height = max(GetHeight(t->left), GetHeight(t->right)) + 1;
    q->height = max(GetHeight(q->left), GetHeight(q->right)) + 1;
    return q;
}

//单旋转
//右右插入导致的不平衡
template <typename T>
AvlNode<T> * AvlTree<T>::RR(AvlNode<T> *t)
{
    AvlNode<T> *q = t->right;
    t->right = q->left;
    q->left = t;
    t = q;
    t->height = max(GetHeight(t->left), GetHeight(t->right)) + 1;
    q->height = max(GetHeight(q->left), GetHeight(q->right)) + 1;
    return q;
}

//双旋转
//插入点位于t的左儿子的右子树
template <typename T>
AvlNode<T> * AvlTree<T>::LR(AvlNode<T> *t)
{
    //双旋转可以通过两次单旋转实现
    //对t的左结点进行RR旋转，再对根节点进行LL旋转
    RR(t->left);
    return LL(t);
}

//双旋转
//插入点位于t的右儿子的左子树
template <typename T>
AvlNode<T> * AvlTree<T>::RL(AvlNode<T> *t)
{
    LL(t->right);
    return RR(t);
}

template <typename T>
void AvlTree<T>::Insert(AvlNode<T> *&t, T x)
{
    if (t == NULL)
        t = new AvlNode<T>(x);
    else if (x < t->data)
    {
        Insert(t->left, x);
        //判断平衡情况
        if (GetHeight(t->left) - GetHeight(t->right) > 1)
        {
            //分两种情况 左左或左右

            if (x < t->left->data)//左左
                t = LL(t);
            else                  //左右
                t = LR(t);
        }
    }
    else if (x > t->data)
    {
        Insert(t->right, x);
        if (GetHeight(t->right) - GetHeight(t->left) > 1)
        {
            if (x > t->right->data)
                t = RR(t);
            else
                t = RL(t);
        }
    }
    else
        ;//数据重复
    t->height = max(GetHeight(t->left), GetHeight(t->right)) + 1;
}

template <typename T>
bool AvlTree<T>::Delete(AvlNode<T> *&t, T x)
{
    //t为空 未找到要删除的结点
    if (t == NULL)
        return false;
    //找到了要删除的结点
    else if (t->data == x)
    {
        //左右子树都非空
        if (t->left != NULL && t->right != NULL)
        {//在高度更大的那个子树上进行删除操作

            //左子树高度大，删除左子树中值最大的结点，将其赋给根结点
            if (GetHeight(t->left) > GetHeight(t->right))
            {
                t->data = FindMax(t->left)->data;
                Delete(t->left, t->data);
            }
            else//右子树高度更大，删除右子树中值最小的结点，将其赋给根结点
            {
                t->data = FindMin(t->right)->data;
                Delete(t->right, t->data);
            }
        }
        else
        {//左右子树有一个不为空，直接用需要删除的结点的子结点替换即可
            AvlNode<T> *old = t;
            t = t->left ? t->left: t->right;//t赋值为不空的子结点
            delete old;
        }
    }
    else if (x < t->data)//要删除的结点在左子树上
    {
        //递归删除左子树上的结点
        Delete(t->left, x);
        //判断是否仍然满足平衡条件
        if (GetHeight(t->right) - GetHeight(t->left) > 1)
        {
            if (GetHeight(t->right->left) > GetHeight(t->right->right))
            {
                //RL双旋转
                t = RL(t);
            }
            else
            {//RR单旋转
                t = RR(t);
            }
        }
        else//满足平衡条件 调整高度信息
        {
            t->height = max(GetHeight(t->left), GetHeight(t->right)) + 1;
        }
    }
    else//要删除的结点在右子树上
    {
        //递归删除右子树结点
        Delete(t->right, x);
        //判断平衡情况
        if (GetHeight(t->left) - GetHeight(t->right) > 1)
        {
            if (GetHeight(t->left->right) > GetHeight(t->left->left))
            {
                //LR双旋转
                t = LR(t);
            }
            else
            {
                //LL单旋转
                t = LL(t);
            }
        }
        else//满足平衡性 调整高度
        {
            t->height = max(GetHeight(t->left), GetHeight(t->right)) + 1;
        }
    }

    return true;
}

//查找结点
template <typename T>
bool AvlTree<T>::Contains(AvlNode<T> *t, const T x) const
{
    if (t == NULL)
        return false;
    if (x < t->data)
        return Contains(t->left, x);
    else if (x > t->data)
        return Contains(t->right, x);
    else
        return true;
}

//中序遍历
template <typename T>
void AvlTree<T>::InorderTraversal(AvlNode<T> *t)
{
    if (t)
    {
        InorderTraversal(t->left);
        cout << t->data << ' ';
        InorderTraversal(t->right);
    }
}

//前序遍历
template <typename T>
void AvlTree<T>::PreorderTraversal(AvlNode<T> *t)
{
    if (t)
    {
        cout << t->data << ' ';
        PreorderTraversal(t->left);
        PreorderTraversal(t->right);
    }
}

main.cpp

#include "AvlTree.h"

int main()
{
    AvlTree<int> tree;
    int value;
    int tmp;
    cout << "请输入整数建立二叉树(-1结束)：" << endl;
    while (cin >> value)
    {
        if (value == -1)
            break;
        tree.Insert(tree.root,value);
    }
    cout << "中序遍历";
    tree.InorderTraversal(tree.root);
    cout << "\n前序遍历:";
    tree.PreorderTraversal(tree.root);
    cout << "\n请输入要查找的结点：";
    cin >> tmp;
    if (tree.Contains(tree.root, tmp))
        cout << "已查找到" << endl;
    else
        cout << "值为" << tmp << "的结点不存在" << endl;
    cout << "请输入要删除的结点：";
    cin >> tmp;
    tree.Delete(tree.root, tmp);
    cout << "删除后的中序遍历：";
    tree.InorderTraversal(tree.root);
    cout << "\n删除后的前序遍历：";
    tree.PreorderTraversal(tree.root);
}

测试结果

以上就是详解如何用c++实现平衡二叉树的详细内容，更多关于c++平衡二叉树的资料请关注我们其它相关文章！