C语言实例真题讲解数据结构中单向环形链表
目录
- 1、例题引入
- 2、何为带环链表
- 3、题解思路
- 4、拓展问题
目录
1、例题引入
链接直达：
题目：
2、何为带环链表
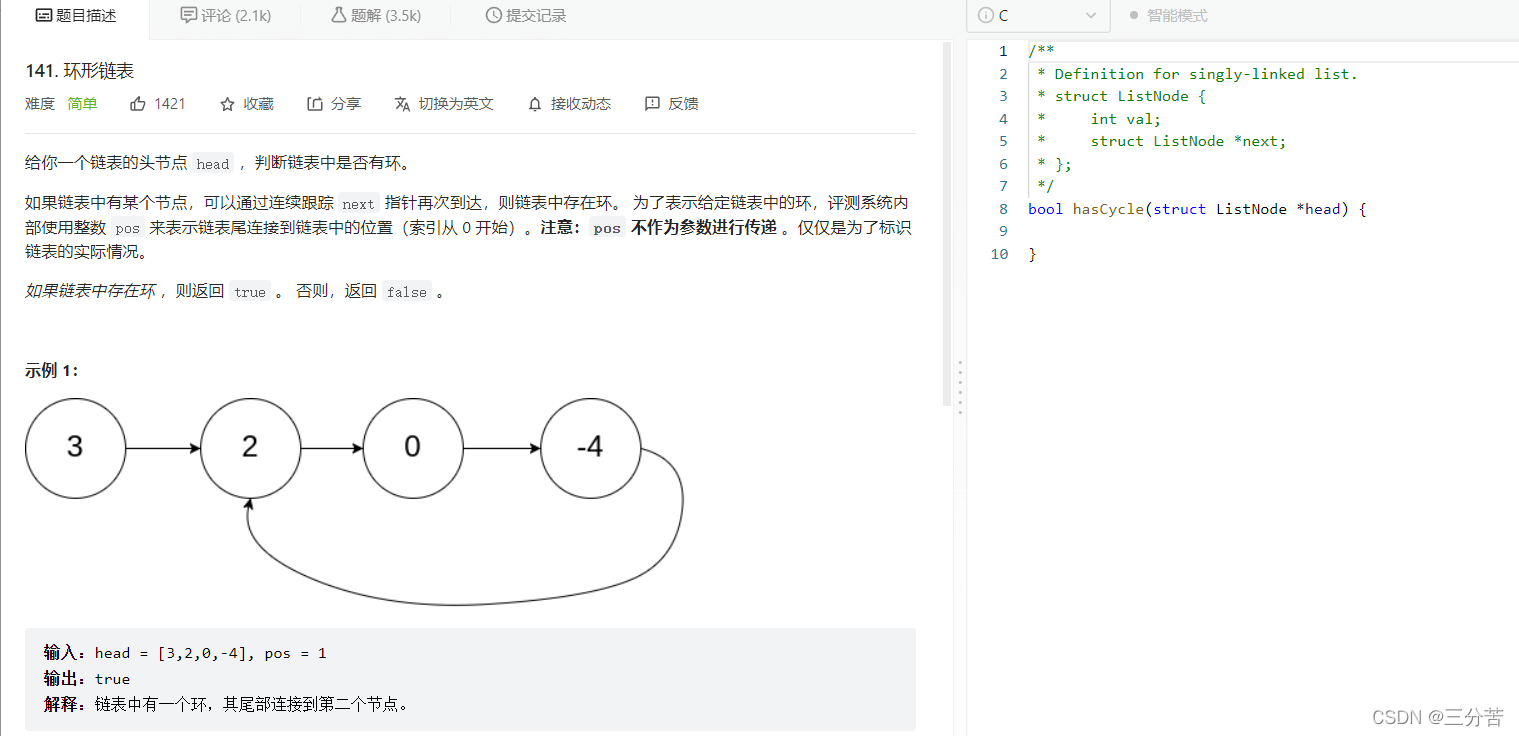
正常的单链表每个节点顺次链接，最后一个节点指向NULL，如下：
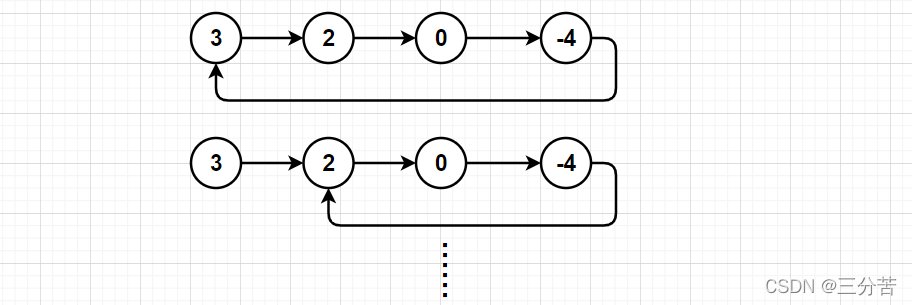
而带环链表的最后一个节点不再指向NULL了，指向的是前面任意一个节点，以此形成带环链表，并一直循环下去。如下：
3、题解思路
我们可以将上述图画的抽象一点，在没有进入环之前我们用直线表示，进入环之后用圈来表示，以此示意循环。此题需要用到我们之前讲解的求中间节点和求倒数第k个节点的快慢指针的思想。定义两个指针slow和fast均指向一开始的位置。 让slow一次走一步，fast一次走两步。
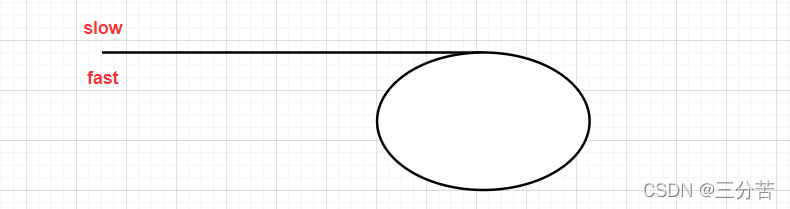
当slow走到直线一半的位置时，此时的fast刚好就在环的入口点。
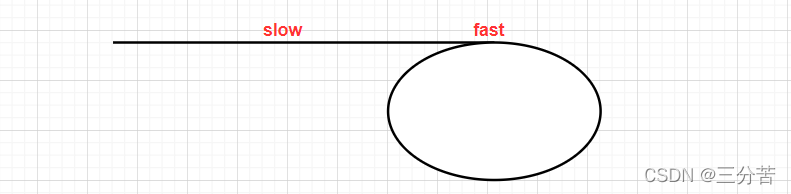
假设slow刚好走到环的入口点时，fast走到如下位置，此时fast开始追赶模式
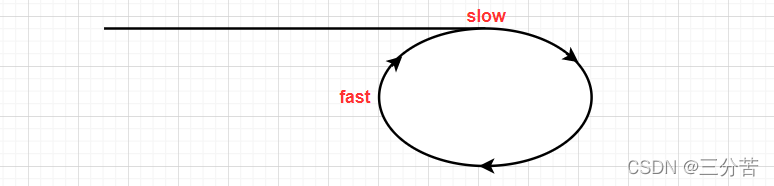
fast开始追赶slow，假设fast在如下的位置开始追上slow
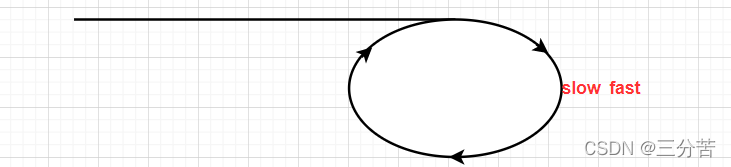
代码如下：
bool hasCycle(struct ListNode *head) {
struct ListNode*slow=head;
struct ListNode*fast=head;
while(fast&&fast->next)
{
slow=slow->next;
fast=fast->next->next;
if(slow==fast)
{
return true;
}
}
return false;
}
单纯从解体的角度看，此题并不复杂，仅需用到快慢指针的思想即可解决，单是由此题可以引出多个值得我们探讨的问题，以此来加深我们对环形链表的认知，如下三大拓展问题：
4、拓展问题
- （1）slow一次走1步，fast一次走2步，一定能追上吗？
答案：一定能。
证明：
当slow走到中间的时候，fast一定进环了，此时fast开始追击。我们假设slow进环以后，slow和fast的距离是N，此时slow走1步，fast走2步，它们俩的距离缩短1变为N-1。以此类推，每次追击，距离缩小1，当距离缩小为0时就追上了。综上，一定能追上。
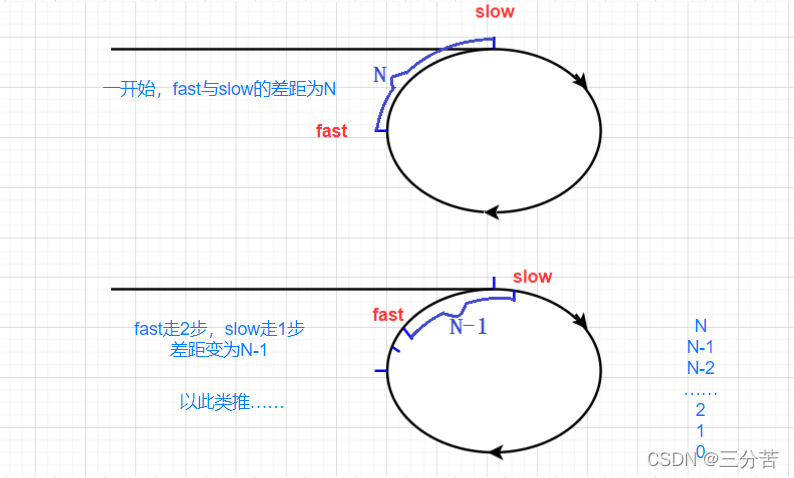
- （2）slow一次走1步，fast一次走3步，能追上吗？fast一次走4步呢？n步呢？
答案：不一定
证明：
我们先来讨论slow一次走1步，fast一次走3步的情况。假设slow走了1步，fast走3步时刚好进环，而当slow刚好进环的时候，fast可能已经走了1圈，具体情况得看环的大小，此时slow和fast之间的距离为N。并假设环的长度是C。
slow一次走1步，fast一次走3步，距离变为N-2。由此可见，fast和slow每走一次，距离缩短2。此时就不难发现了，需要分类讨论，当N是偶数时，刚好可以追上，当N是奇数时，追到最后距离为-1，此时就要再追了，意味着slow和fast之间的距离变成C-1。
继续追击，根据前面的分析，如果C-1是偶数，那么可以追上。如果C-1是奇数，那么就永远追不上了，将会无线循环追下去，可就是追不上。他们的差距N是由进环前的长度和环的长度决定的，而这两个又都是随机的，所以N的值不确定，可奇可偶，又像刚刚那样讨论下去，出现奇数将一去不复返。
同理fast一次走4步也是这样的讨论，同样都是不一定，不过这个时候是每走一次，距离缩短3。当N是3的倍数就可以追上，当不是3的倍数就要继续讨论了，有兴趣的童鞋可以继续钻研下去，思想和fast一次走3步一样，这里不过多赘述。
- （3）链表环的入口点在哪呢？
当我们搞清楚slow和fast分别走的距离时，入口点自然就明了了。
法一：
slow一次走1步，fast一次走2步，那么fast走的距离是slow的2倍
在具体讲解之前，首先要搞清楚，不存在说慢指针slow在里头走了一圈，快指针fast还没有追到slow，因为fast每次走2步，slow每次走1步，它俩间的距离每次都缩小1，所以只会越来越近，直到追到。最多最多也就快1圈，但从来也不会刚好满1圈。所以下面很容易推出slow和fast分别走了多少。
假设：
【链表头 - - - 入口点】：L
【入口点 - - - 相遇点】：X
【环的长度】：C
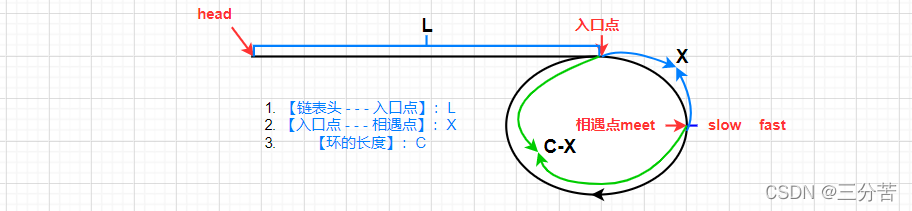
slow走的距离：L + X
fast走的距离：L + N*C + X
解释：
因为先前已经提到slow不会都走了一圈还没被追到，所以很容易推出slow的距离就是L+X
而快指针一次走2步，很可能会因为环过小导致在slow指针进入入口点前，fast指针已经走了好几圈。简而言之3句话：
- L很小，C很大，slow进环前，fast可能在环里面，一圈都没走完
- L很大，C很小，slow进环前，fast在里面走了很多圈了
- 但是slow进环以后，在一圈之内，fast一定追到slow，它们的距离最多C-1
根据一开始说的，fast走的距离是slow走的距离的2倍，可列出如下式子：
2*(L+X) = L + N*C + X
化简后：L+X = N*C 或 L = N*C - X 或 L = (N-1)*C + (C-X) 或 L + X = N*C
用此公式即可证明：一个指针从meet走，一个指针从head走，他们会在入口点相遇！
因为式子(N-1)*C表明从相遇点走了N-1圈后又回到了相遇点，此时再走C-X的距离就回到了入口点，由上得知，此公式确实让它们回到了入口点。
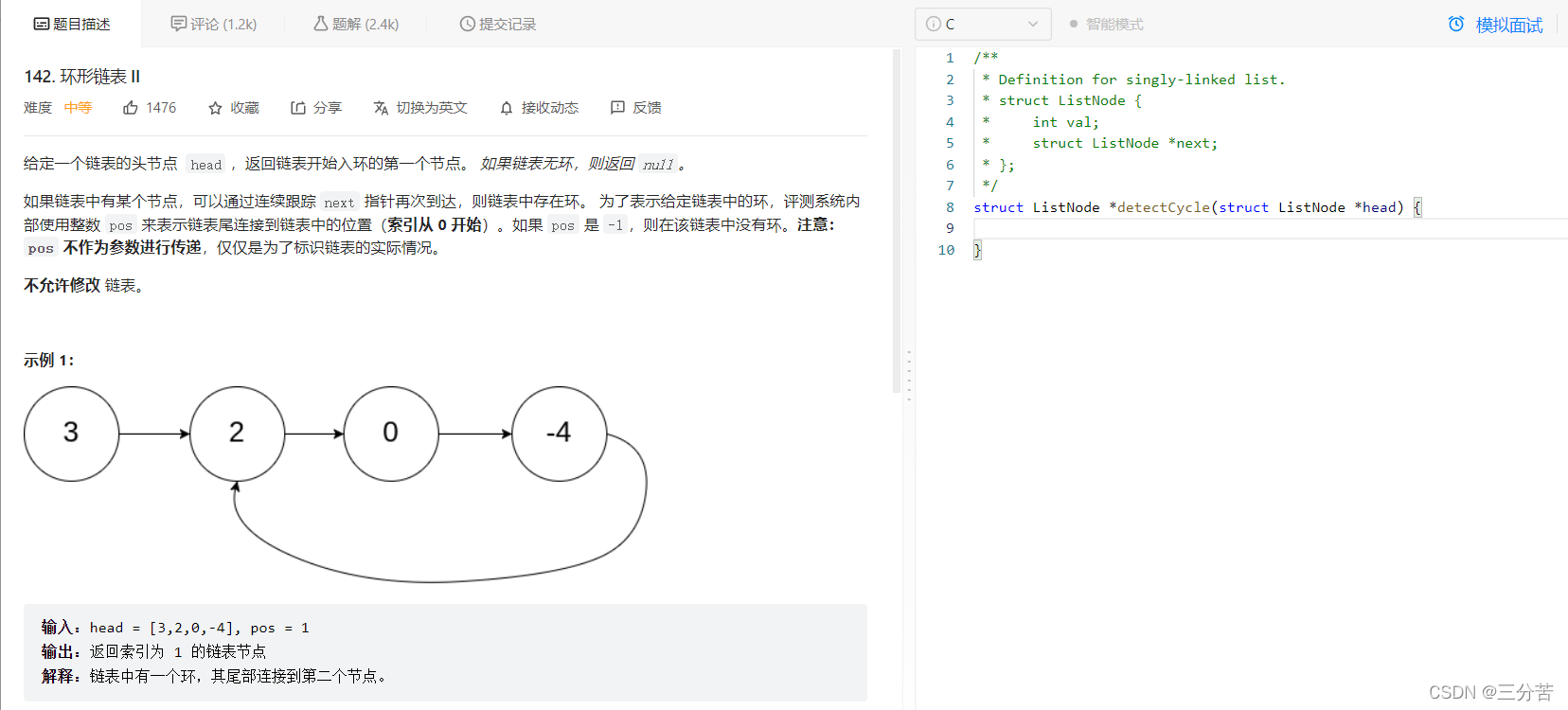
用一道切实的题目来具体解出入口点的位置：链接直达：
题目：
代码如下：
struct ListNode* detectCycle(struct ListNode* head) {
struct ListNode* slow = head;
struct ListNode* fast = head;
while (fast && fast->next)
{
//判断是否是带环链表
slow = slow->next;
fast = fast->next->next;
if (slow == fast)
{
struct ListNode* meet = slow;
while (meet != head)
{
//求出相遇点
meet = meet->next;
head = head->next;
}
return meet;
}
}
return NULL;
}
求相遇点还有另外一种方法：
找到相遇点meet后，让meet做尾，让下一个点做新链表的头
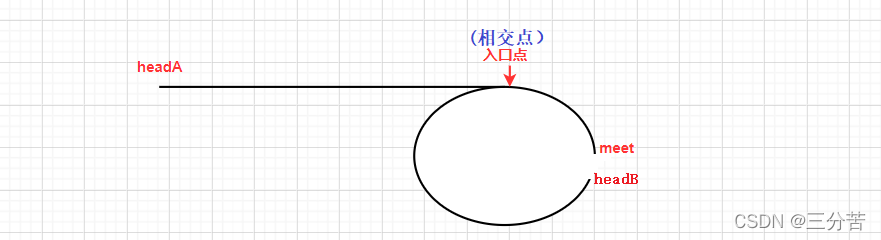
此法显的尤为巧妙，刚好转换成了两个链表求交点的问题。因为此时headA链表的尾部是meet，而headB链表的尾部也是meet，此时就意味着俩链表必会相交，而相交的地方就是入口点，两链表相交正是博主上篇博文中所详细讲解的，这里就不过多强调了。
到此这篇关于C语言超详细讲解数据结构中单向环形链表的文章就介绍到这了,更多相关C语言 单向环形链表内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！
相关推荐
-
C语言数据结构之单向链表详解分析
链表的概念:链表是一种动态存储分布的数据结构,由若干个同一结构类型的结点依次串连而成. 链表分为单向链表和双向链表. 链表变量一般用指针head表示,用来存放链表首结点的地址. 每个结点由数据部分和下一个结点的地址部分组成,即每个结点都指向下一个结点.最后一个结点称为表尾,其下一个结点的地址部分的值为NULL(表示为空地址). 特别注意:链表中的各个结点在内存中是可以不连续存放的,具体存放位置由系统分配. 例如:int *ptr ; 因此不可以用ptr++的方式来寻找下一个结点. 使用链表的优点
-
C语言实现带头双向循环链表
目录 前言 1. 创建结构体 2.malloc新节点 3.创建哨兵位节点 4.尾插 5.打印 6.尾删 7.头插 8.在指定位置pos的前面进行插入 9. 删除指定位置pos节点 10.销毁链表 前言 在实际生活中最常用的就是这两种链表.无头单向非循环链表.和带头双向循环链表.无头单向非循环链表:结构简单,一般不会单独用来存数据.实际中更多是作为其他数据结构的子结构,如哈希桶.图的邻接表等等.另外这种结构在笔试面试中出现很多.带头双向循环链表:结构最复杂,一般用在单独存储数据.实际中使用的链表数
-
C语言单向链表的表示与实现实例详解
1.概述: C语言中的单向链表(单链表)是链表的一种,其特点是链表的链接方向是单向的,对链表的访问要通过顺序读取从头部开始. 链表中最简单的一种是单向链表,它包含两个域,一个信息域和一个指针域.这个链接指向列表中的下一个节点,而最后一个节点则指向一个空值. 如下图所示: 一个单向链表包含两个值: 当前节点的值和一个指向下一个节点的链接 一个单向链表的节点被分成两个部分.第一个部分保存或者显示关于节点的信息,第二个部分存储下一个节点的地址.单向链表只可向一个方向遍历. 链表最基本的结构是在每个节点
-
C语言实现带头双向环形链表
双向循环链表 上一次我们讲了单向无头非循环链表的实现,单向无头非循环链表的特点是:结构简单,一般不会单独用来存数据.实际中更多是作为其他数据结构的子结构.而带头双向循环链表则恰恰与无头单向非循环链表相反,它的结构最复杂,一般用来单独存储数据.这个结构虽然复杂,但是使用单吗实现后会发现,这个结构用起来很简单. 结构示意图 带头双向循环链表在逻辑上大概就是这样的一个样子,链表的最后一个节点的后继指向的是头结点.而头结点的前驱则是指向链表的最后一个结点.所以,一个空的带头双向循环链表的逻辑结构应该是这
-
C语言实现无头单向链表的示例代码
目录 一.易错的接口实现 1.1 新节点开辟函数 1.2 尾插 1.3 尾删 二.常见简单接口 2.1 打印链表 2.2 节点计数器 2.3 判断是否为空链表 2.4 通过值查找节点 2.5 头插 2.6 头删 2.7 在任意节点后插入节点 2.8 在任意节点后删除节点 2.9 销毁链表 三.头文件相关内容 3.1 引用的库函数 3.2 结构体声明 一.易错的接口实现 1.1 新节点开辟函数 由于创建一个新节点是频繁的操作,所以封装为一个接口最佳. 链表节点的属性有:(1)数值.(2)指向下一个
-
C语言超详细讲解数据结构中双向带头循环链表
目录 一.概念 二.必备工作 2.1.创建双向链表结构 2.2.初始化链表 2.3.动态申请节点 2.4.打印链表 2.5.销毁链表 三.主要功能 3.1.在pos节点前插入数据 尾插 头插 3.2.删除pos处节点数据 尾删 头删 3.3.查找数据 四.总代码 List.h 文件 List.c 文件 Test.c 文件 五.拓展 一.概念 前文我们已经学习了单向链表,并通过oj题目深入了解了带头节点的链表以及带环链表,来画张图总体回顾下: 在我们学习的链表中,其实总共有8种,都是单双向和带不带
-
C语言数据结构超详细讲解单向链表
目录 1.链表概况 1.1 链表的概念及结构 1.2 链表的分类 2. 单向链表的实现 2.1 SList.h(头文件的汇总,函数的声明) 2.2 SList.c(函数的具体实现逻辑) 2.2.1 打印链表 2.2.2 搞出一个新节点(为其他函数服务) 2.2.3 链表尾插 2.2.4 链表头插 2.2.5 链表尾删 2.2.6 链表头删 2.2.7 查找节点 2.2.8 在pos位置之前插入 2.2.9 在pos位置之后插入 2.2.10 删除pos位置 2.2.11 删除pos之后位置 2.
-
C语言之单向链表详解及实例代码
1,单向链简洁. 单向链表(单链表)是链表的一种,其特点是链表的链接方向是单向的,对链表的访问要通过顺序读取从头部开始:链表是使用指针进行构造的列表:又称为结点列表,因为链表是由一个个结点组装起来的:其中每个结点都有指针成员变量指列表中的下一个结点:列表是由结点构成,由head指针指向第一个成为表头的结点而终止于最后一个指向nuLL的指针: 2,例子要求: 根据示例代码中的例子,完成单向链表(single linked list)中的以字符串为数据的链表的插入.删除以及查找,并支持单向链表的反转
-
C语言实例真题讲解数据结构中单向环形链表
目录 1.例题引入 2.何为带环链表 3.题解思路 4.拓展问题 目录 1.例题引入 链接直达: 环形链表 题目: 2.何为带环链表 正常的单链表每个节点顺次链接,最后一个节点指向NULL,如下: 而带环链表的最后一个节点不再指向NULL了,指向的是前面任意一个节点,以此形成带环链表,并一直循环下去.如下: 3.题解思路 我们可以将上述图画的抽象一点,在没有进入环之前我们用直线表示,进入环之后用圈来表示,以此示意循环.此题需要用到我们之前讲解的求中间节点和求倒数第k个节点的快慢指针的思想.定义两
-
C语言超详细讲解数据结构中的线性表
目录 前言 一.分文件编写 1.分文件编写概念 2.代码展示 二.动态分布内存malloc 1.初识malloc 2.使用方法 三.创建链表并进行增删操作 1.初始化链表 2.在链表中增加数据 3.删除链表中指定位置数据 四.代码展示与运行效果 1.代码展示 2.运行效果 总结 前言 计算机专业都逃不了数据结构这门课,而这门课无疑比较难理解,所以结合我所学知识,我准备对顺序表做一个详细的解答,为了避免代码过长,采用分文件编写的形式,不仅可以让代码干净利落还能提高代码可读性,先解释部分代码的含义,
-
C语言单值二叉树真题讲解
目录 一.题目描述 二.解题思路 [OJ - 二叉树]单值二叉树 LeetCode链接:单值二叉树 题目难度:简单 一.题目描述 如果二叉树每个节点都具有相同的值,那么该二叉树就是 单值 二叉树. 只有给定的树是单值二叉树时,才返回 true:否则返回 false. 二.解题思路 二叉树的递归遍历,一般都会把问题拆分成 当前树(根节点) 和 子树,然后子树又进行拆分,来解决问题. 核心思路: 1.先判断当前节点是否为空,如果为空,返回 true(空树也满足单值二叉树的条件) 2.判断当前树是不是
-
Java 超详细讲解数据结构中的堆的应用
目录 一.堆的创建 1.向下调整(以小堆为例) 2.创建堆 3.创建堆的时间复杂度 二.堆的插入和删除 1.堆的插入 2.堆的删除 三.堆的应用 1.堆排序 2.top-k问题 [求最小的K个数] 四.常用接口的介绍 1.PriorityQueue的特性 2.优先级队列的构造 一.堆的创建 1.向下调整(以小堆为例) 让parent标记需要调整的节点,child标记parent的左孩子(注意:parent如果有孩子一定先是有左孩子) 如果parent的左孩子存在,即:child < size,
-
Java 超详细讲解数据结构中的堆的应用
目录 一.堆的创建 1.向下调整(以小堆为例) 2.创建堆 3.创建堆的时间复杂度 二.堆的插入和删除 1.堆的插入 2.堆的删除 三.堆的应用 1.堆排序 2.top-k问题(求最小的K个数) 四.常用接口的介绍 1.PriorityQueue的特性 2.优先级队列的构造 一.堆的创建 1.向下调整(以小堆为例) 让parent标记需要调整的节点,child标记parent的左孩子(注意:parent如果有孩子一定先是有左孩子) 如果parent的左孩子存在,即:child < size, 进
-
C语言平衡二叉树真题练习
目录 一.题目描述 二.解题思路 自顶向下的递归(暴力解法) 自底向上的递归(最优解法) 题目难度:简单 LeetCode链接:平衡二叉树 一.题目描述 给定一个二叉树,判断它是否是高度平衡的二叉树. 本题中,一棵高度平衡二叉树定义为:一个二叉树 每个节点 的左右两个子树的高度差的绝对值不超过 1 . 二.解题思路 一棵二叉树是平衡二叉树,当且仅当其所有子树也都是平衡二叉树,因此我们使用递归的方式依次判断其所有子树是否为平衡二叉树,就知道这棵二叉树是不是平衡二叉树了. 自顶向下的递归(暴力解法)
-
Java数组与二维数组及替换空格实战真题讲解
目录 数组中重复的数字 题目描述 思路详解 代码与结果 二维数组中的查找 题目描述 思路详解 代码与结果 替换空格 题目描述 思路详解 代码与结果 数组中重复的数字 题目描述 思路详解 本题的思路比较简单,首先将这个数组排序,遍历数组,找到当前的和前一个相同的直接输出就好了.没找到输出-1. 注意:这个方法要注意循环的时候下标要从1开始哦,不然会报数组下标异常滴. 代码与结果 import java.util.*; public class Solution { /** * 代码中的类名.方法名
-
Java跳跃游戏实例真题解决思路详解
目录 变式题—跳跃游戏 I 一.题目描述 二.思路 三.代码 变式题—跳跃游戏 II 一.题目描述 二.思路 三.代码 变式题—跳跃游戏 I 一.题目描述 给定一个非负整数数组 nums ,你最初位于数组的 第一个下标 .数组中的每个元素代表你在该位置可以跳跃的最大长度.判断你是否能够到达最后一个下标. 来源:https://leetcode.cn/problems/jump-game/ 示例: 二.思路 本题可以使用贪心法解决,对每个能到达的位置(可覆盖到的位置),计算其每次能覆盖的最大长度,
-
用C语言举例讲解数据结构中的算法复杂度结与顺序表
数据结构算法复杂度 1.影响算法效率的主要因素 (1)算法采用的策略和方法: (2)问题的输入规模: (3)编译器所产生的代码: (4)计算机执行速度. 2.时间复杂度 // 时间复杂度:2n + 5 long sum1(int n) { long ret = 0; \\1 int* array = (int*)malloc(n * sizeof(int)); \\1 int i = 0; \\1 for(i=0; i<n; i++) \\n { array[i] = i + 1; } for(