python实现IOU计算案例

计算两个矩形的交并比，通常在检测任务里面可以作为一个检测指标。你的预测bbox和groundtruth之间的差异，就可以通过IOU来体现。很简单的算法实现，我也随便写了一个，嗯，很简单。

1. 使用时，请注意bbox四个数字的顺序(y0,x0,y1,x1)，顺序不太一样。

#!/usr/bin/env python
# encoding: utf-8

def compute_iou(rec1, rec2):
  """
  computing IoU
  :param rec1: (y0, x0, y1, x1), which reflects
      (top, left, bottom, right)
  :param rec2: (y0, x0, y1, x1)
  :return: scala value of IoU
  """
  # computing area of each rectangles
  S_rec1 = (rec1[2] - rec1[0]) * (rec1[3] - rec1[1])
  S_rec2 = (rec2[2] - rec2[0]) * (rec2[3] - rec2[1])

  # computing the sum_area
  sum_area = S_rec1 + S_rec2

  # find the each edge of intersect rectangle
  left_line = max(rec1[1], rec2[1])
  right_line = min(rec1[3], rec2[3])
  top_line = max(rec1[0], rec2[0])
  bottom_line = min(rec1[2], rec2[2])

  # judge if there is an intersect
  if left_line >= right_line or top_line >= bottom_line:
    return 0
  else:
    intersect = (right_line - left_line) * (bottom_line - top_line)
    return (intersect / (sum_area - intersect))*1.0

if __name__=='__main__':
  rect1 = (661, 27, 679, 47)
  # (top, left, bottom, right)
  rect2 = (662, 27, 682, 47)
  iou = compute_iou(rect1, rect2)
  print(iou)

补充知识：基于Python实现的IOU算法---最简单易懂的代码实现

概念介绍：

交并比:(Intersection over Union)

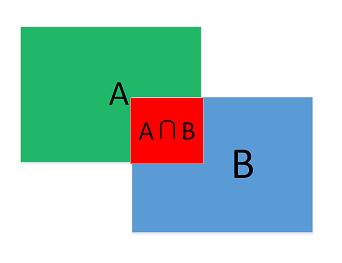
如上图所示，IOU值定位为两个矩形框面积的交集和并集的比值。即:

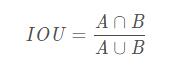
交并比的实现也是非常简单的，执行过程如下：

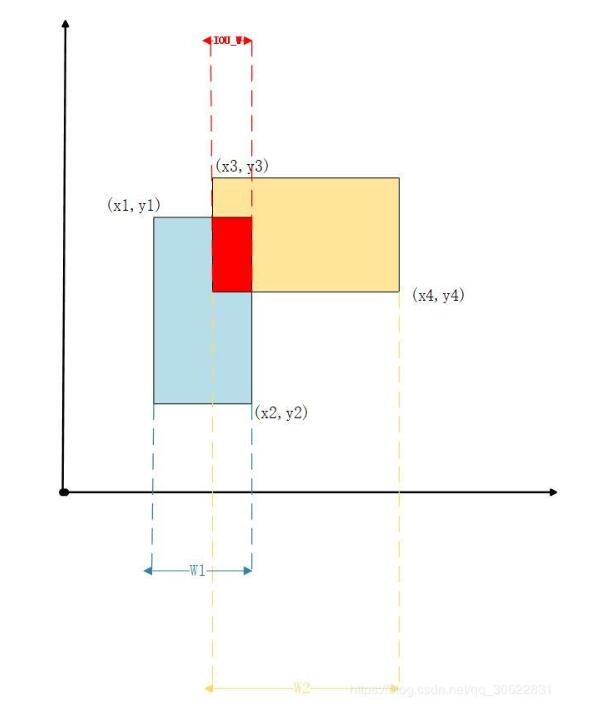
1. 交集形状的宽度计算为：

IOU_W = min(x1,x2,x3,x4)+w1+w2-max(x1,x2,x3,x4)

2. 交集形状的高度计算为：

IOU_H = min(y1,y2,y3,y4)+h1+h2-max(y1,y2,y3,y4)

其实是很简单的几何关系变换，上面的图可以帮助你很好的理解这个意思。

代码实现：001-IOU计算

以上这篇python实现IOU计算案例就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持我们。

赞 (0)

相关推荐

  • python计算二维矩形IOU实例

    计算交并比:交的面积除以并的面积. 要求矩形框的长和宽应该平行于图片框.不然不能用这样的公式计算. 原理,从一维上来理解:两条红线的距离之和减去黑色线之间的距离就是相交的距离.两条红线之和很容易算,两条黑线之间的距离就是最小的起点到到最大的末点,最小的起点好算,最大的末点就是两点加上各自长度之后的最大值.这就算出了一维的情况,二维的情况一样,计算二次而已. def iou(rect1,rect2): ''' 计算两个矩形的交并比 :param rect1:第一个矩形框.表示为x,y,w,h,其中

  • python shapely.geometry.polygon任意两个四边形的IOU计算实例

    在目标检测中一个很重要的问题就是NMS及IOU计算,而一般所说的目标检测检测的box是规则矩形框,计算IOU也非常简单,有两种方法: 1. 两个矩形的宽之和减去组合后的矩形的宽就是重叠矩形的宽,同比重叠矩形的高 2. 右下角的minx减去左上角的maxx就是重叠矩形的宽,同比高 然后 IOU = 重叠面积 / (两矩形面积和-重叠面积) 然,不规则四边形就不能通过这种方式来计算,找了好久数学资料,还是没找到答案(鄙人数学渣渣),最后看了白翔老师的textBoxes++论文源码后,知道python

  • Python计算机视觉里的IOU计算实例

    其中x1,y1;x2,y2分别表示两个矩形框的中心点 def calcIOU(x1, y1, w1, h1, x2, y2, w2, h2): if((abs(x1 - x2) < ((w1 + w2)/ 2.0)) and (abs(y1-y2) < ((h1 + h2)/2.0))): left = max((x1 - (w1 / 2.0)), (x2 - (w2 / 2.0))) upper = max((y1 - (h1 / 2.0)), (y2 - (h2 / 2.0))) righ

  • python实现的Iou与Giou代码

    最近看了网上很多博主写的iou实现方法,但Giou的代码似乎比较少,于是便自己写了一个,新手上路,如有错误请指正,话不多说,上代码: def Iou(rec1,rec2): x1,x2,y1,y2 = rec1 #分别是第一个矩形左右上下的坐标 x3,x4,y3,y4 = rec2 #分别是第二个矩形左右上下的坐标 area_1 = (x2-x1)*(y1-y2) area_2 = (x4-x3)*(y3-y4) sum_area = area_1 + area_2 w1 = x2 - x1#第

  • 浅谈Python3实现两个矩形的交并比(IoU)

    一.前言 因为最近刚好被问到这个问题,但是自己当时特别懵逼,导致没有做出来.所以下来后自己Google了很多IoU的博客,但是很多博客要么过于简略,要么是互相转载的,有一些博客图和代码还有点问题,也导致自己这个萌新走了不少弯路.所以自己重新整理了看的博客,力求以更简单的方式展现这个问题的解答办法,方便日后自己回顾.如果朋友们觉得写的有问题的地方,非常欢迎大家在下面留言交流,避免因为我的问题导致读者走弯路. 二.交并比的概念及应用 假设平面坐标中有一个矩形,并且这个矩形的长和宽均分别与x轴和y轴平

  • python:目标检测模型预测准确度计算方式(基于IoU)

    训练完目标检测模型之后,需要评价其性能,在不同的阈值下的准确度是多少,有没有漏检,在这里基于IoU(Intersection over Union)来计算. 希望能提供一些思路,如果觉得有用欢迎赞我表扬我~ IoU的值可以理解为系统预测出来的框与原来图片中标记的框的重合程度.系统预测出来的框是利用目标检测模型对测试数据集进行识别得到的. 计算方法即检测结果DetectionResult与GroundTruth的交集比上它们的并集,如下图: 蓝色的框是:GroundTruth 黄色的框是:Dete

  • python不使用for计算两组、多个矩形两两间的iou方式

    解决问题: 不使用for计算两组.多个矩形两两间的iou 使用numpy广播的方法,在python程序中并不建议使用for语句,python中的for语句耗时较多,如果使用numpy广播的思想将会提速不少. 代码: def calc_iou(bbox1, bbox2): if not isinstance(bbox1, np.ndarray): bbox1 = np.array(bbox1) if not isinstance(bbox2, np.ndarray): bbox2 = np.arr

  • python实现IOU计算案例

    计算两个矩形的交并比,通常在检测任务里面可以作为一个检测指标.你的预测bbox和groundtruth之间的差异,就可以通过IOU来体现.很简单的算法实现,我也随便写了一个,嗯,很简单. 1. 使用时,请注意bbox四个数字的顺序(y0,x0,y1,x1),顺序不太一样. #!/usr/bin/env python # encoding: utf-8 def compute_iou(rec1, rec2): """ computing IoU :param rec1: (y0

  • 如何通过python实现IOU计算代码实例

    Intersection over Union(IOU)是一种测量在特定数据集中检测相应物体准确度的一个标准.IoU是一个简单的测量标准,只要是在输出中得出一个预测范围(bounding boxes)的任务都可以用IoU来进行测量. IoU分数是对象类别分割问题的标准性能度量 [1] . 给定一组图像,IoU测量给出了在该组图像中存在的对象的预测区域和地面实况区域之间的相似性 计算两个矩形的交并比,通常在检测任务里面可以作为一个检测指标.你的预测bbox和groundtruth之间的差异,就可以

  • 使用Python三角函数公式计算三角形的夹角案例

    题目内容: 对于三角形,三边长分别为a, b, c,给定a和b之间的夹角C,则有:.编写程序,使得输入三角形的边a, b, c,可求得夹角C(角度值). 输入格式: 三条边a.b.c的长度值,每个值占一行. 输出格式: 夹角C的值,保留1位小数. 输入样例: 3 4 5 输出样例: 90.0 code: import math a = float(eval(input('请输入a的边长'))) b = float(eval(input('请输入b的边长'))) c = float(eval(in

  • 详解Python OpenCV数字识别案例

    详解Python OpenCV数字识别案例

    前言 实践是检验真理的唯一标准. 因为觉得一板一眼地学习OpenCV太过枯燥,于是在网上找了一个以项目为导向的教程学习.话不多说,动手做起来. 一.案例介绍 提供信用卡上的数字模板: 要求:识别出信用卡上的数字,并将其直接打印在原图片上.虽然看起来很蠢,但既然可以将数字打印在图片上,说明已经成功识别数字,因此也可以将其转换为数字文本保存.车牌号识别等项目的思路与此案例类似. 示例: 原图 处理后的图 二.步骤 大致分为如下几个步骤: 1.模板读入 2.模板预处理,将模板数字分开,并排序 3.输入

  • python实现CTC以及案例讲解

    python实现CTC以及案例讲解

    在大多数语音识别任务中,我们都缺少文本和音频特征的alignment,Connectionist Temporal Classification作为一个损失函数,用于在序列数据上进行监督式学习,可以不需要对齐输入数据及标签. 对于输入序列 X = [ x 1 , x 2 , . . , x T ] X=[x_1, x_2, .., x_T] X=[x1​,x2​,..,xT​] 和 输出序列 Y = [ y 1 , y 2 , . . . , y U ] Y = [y_1, y_2, ...,

  • Python 概率生成问题案例详解

    概率生成问题 有一枚不均匀的硬币,要求产生均匀的概率分布 有一枚均匀的硬币,要求产生不均匀的概率分布,如 0.25 和 0.75 利用 Rand7() 实现 Rand10() 不均匀硬币 产生等概率 现有一枚不均匀的硬币 coin(),能够返回 0.1 两个值,其概率分别为 0.6.0.4.要求使用这枚硬币,产生均匀的概率分布.即编写一个函数 coin_new() 使得它返回 0.1 的概率均为 0.5. # 不均匀硬币,返回 0.1 的概率分别为 0.6.0.4 def coin(): ret

  • 7个关于Python的经典基础案例

    目录 1.列表排序 2.调换字典键值 3.删除列表中的重复元素 4.输出质数 5.判断是一年中第几天 6.猜数字 7.进制转换 1.列表排序 def que6(): # 6.输入三个整数x, y, z,形成一个列表,请把这n个数由小到大输出. # 程序分析:列表有sort方法,所以把他们组成列表即可. li = np.random.randint(-100, 100, size=10) # 就地转化 li = li.tolist() # 用sort()结果 li_sort = sorted(li

  • python学习实操案例(三)

    python学习实操案例(三)

    目录 任务1.循环输出26个字母对应的ASCII码值 任务2.模拟用户登录 任务3.猜数游戏 任务4.计算100-999之间的水仙花数 任务1.循环输出26个字母对应的ASCII码值 x=97#代表的是a的ASCII值 for _ in range(1,27):     print(chr(x),'----->',x)     x+=1 print('--------------------------------------') x=97 while x<123:     print(chr

随机推荐