Java深入分析了解平衡二叉树

目录

• AVL树的引入
• 基本概念
• 基础设计
• RR(左旋)
• LL(右旋)
• LR(先左旋再右旋)
• RL(先右旋再左旋)
• 添加节点
• 删除节点

AVL树的引入

搜索二叉树有着极高的搜索效率，但是搜索二叉树会出现以下极端情况：

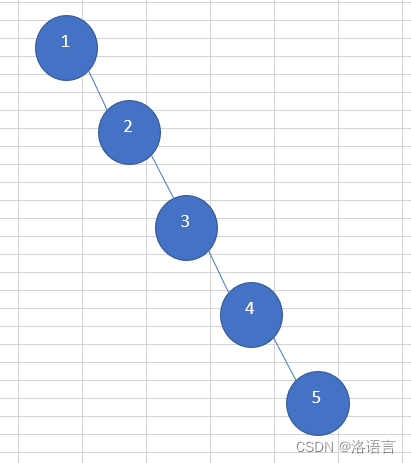
这样的二叉树搜索效率甚至比链表还低。在搜索二叉树基础上出现的平衡二叉树(AVL树)就解决了这样的问题。当平衡二叉树(AVL树)的某个节点左右子树高度差的绝对值大于1时，就会通过旋转操作减小它们的高度差。

基本概念

AVL树本质上还是一棵二叉搜索树，它的特点是：

• 本身首先是一棵二叉搜索树。
• 每个结点的左右子树的高度之差的绝对值（平衡因子）最多为1。也就是说，AVL树，本质上是带了平衡功能的二叉查找树（二叉排序树，二叉搜索树）。
• 当插入一个节点或者删除一个节点时，导致某一个节点的左右子树高度差的绝对值大于1，这时需要通过左旋和右旋的操作使二叉树再次达到平衡状态。

平衡因子(balanceFactor)

• 一个结点的左子树与右子树的高度之差。
• AVL树中的任意结点的BF只可能是-1，0和1。

基础设计

下面是AVL树需要的简单方法和属性：

public class AVLTree <E extends Comparable<E>>{
    class Node{
        E value;
        Node left;
        Node right;
        int height;
        public Node(){}
        public Node(E value){
            this.value = value;
            height = 1;
            left = null;
            right = null;
        }
        public void display(){
            System.out.print(this.value + " ");
        }
    }
    Node root;
    int size;
    public int size(){
        return size;
    }
    public int getHeight(Node node) {
        if(node == null) return 0;
        return node.height;
    }
    //获取平衡因子(左右子树的高度差，大小为1或者0是平衡的，大小大于1不平衡)
    public int getBalanceFactor(){
        return getBalanceFactor(root);
    }
    public int getBalanceFactor(Node node){
        if(node == null) return 0;
        return getHeight(node.left) - getHeight(node.right);
    }
    //判断一个树是否是一个平衡二叉树
    public boolean isBalance(Node node){
        if(node == null) return true;
        int balanceFactor = Math.abs(getBalanceFactor(node.left) - getBalanceFactor(node.right));
        if(balanceFactor > 1) return false;
        return isBalance(node.left) && isBalance(node.right);
    }
    public boolean isBalance(){
        return isBalance(root);
    }
    //中序遍历树
    private  void inPrevOrder(Node root){
        if(root == null) return;
        inPrevOrder(root.left);
        root.display();
        inPrevOrder(root.right);
    }
    public void inPrevOrder(){
        System.out.print("中序遍历：");
        inPrevOrder(root);
    }
}

RR(左旋)

往一个树右子树的右子树上插入一个节点，导致二叉树变得不在平衡，如下图，往平衡二叉树中插入5，导致这个树变得不再平衡，此时需要左旋操作，如下：

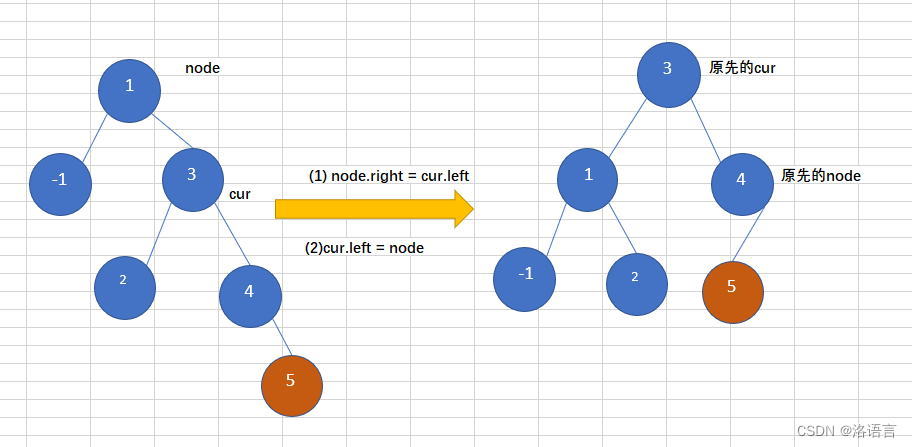
代码如下：

//左旋,并且返回新的根节点
    public Node leftRotate(Node node){
        System.out.println("leftRotate");
       Node cur = node.right;
       node.right = cur.left;
       cur.left = node;
       //跟新node和cur的高度
        node.height = Math.max(getHeight(node.left),getHeight(node.right)) + 1;
        cur.height = Math.max(getHeight(cur.left),getHeight(cur.right)) + 1;
        return cur;
    }

LL(右旋)

往一个AVL树左子树的左子树上插入一个节点，导致二叉树变得不在平衡，如下图，往平衡二叉树中插入2，导致这个树变得不再平衡，此时需要左旋操作，如下：

代码如下：

 //右旋，并且返回新的根节点
    public Node rightRotate(Node node){
        System.out.println("rightRotate");
        Node cur = node.left;
        node.left = cur.right;
        cur.right = node;
        //跟新node和cur的高度
        node.height = Math.max(getHeight(node.left),getHeight(node.right)) + 1;
        cur.height = Math.max(getHeight(cur.left),getHeight(cur.right)) + 1;
        return cur;
    }

LR(先左旋再右旋)

往AVL树左子树的右子树上插入一个节点，导致该树不再平衡，需要先对左子树进行左旋，再对整棵树右旋，如下图所示，插入节点为5.

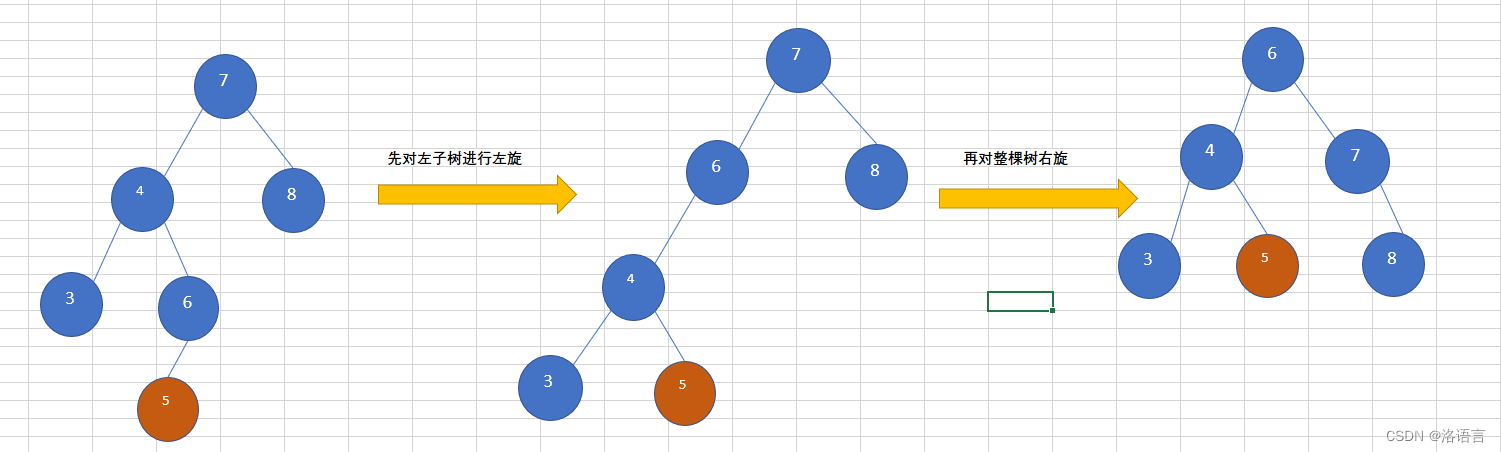
RL(先右旋再左旋)

往AVL树右子树的左子树上插入一个节点，导致该树不再平衡，需要先对右子树进行右旋，再对整棵树左旋，如下图所示，插入节点为2.

添加节点

//添加元素
    public  void add(E e){
        root = add(root,e);
    }
    public Node add(Node node, E value) {
        if (node == null) {
            size++;
            return new Node(value);
        }
        if (value.compareTo(node.value) > 0) {
            node.right = add(node.right, value);
        } else if (value.compareTo(node.value) < 0) {
            node.left = add(node.left, value);
        }
        //跟新节点高度
        node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
        //获取当前节点的平衡因子
        int balanceFactor = getBalanceFactor(node);
        //该子树不平衡且新插入节点(导致不平衡的节点)在左子树的左子树上，此时需要进行右旋
        if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0) {
            return rightRotate(node);
        }
        //该子树不平衡且新插入节点(导致不平衡的节点)在右子树子树的右子树上，此时需要进行左旋
        else if (balanceFactor < -1 && getBalanceFactor(node.right) <= 0) {
            return leftRotate(node);
        }
        //该子树不平衡且新插入节点(导致不平衡的节点)在左子树的右子树上，此时需要先对左子树左旋，在整个树右旋
        else if (balanceFactor > 1 && getBalanceFactor(node.left) < 0) {
            node.left = leftRotate(node.left);
            return rightRotate(node);
        }
        //balanceFactor < -1 && getBalanceFactor(node.left) > 0
        //该子树不平衡且新插入节点(导致不平衡的节点)在右子树的左子树上，此时需要先对右子树右旋，再整个树左旋
        else if(balanceFactor < -1 && getBalanceFactor(node.right) > 0) {
            node.right = rightRotate(node.right);
            return leftRotate(node);
        }
        return node;
    }

删除节点

 //删除节点
    public E remove(E value){
        root = remove(root,value);
        if(root == null){
            return null;
        }
        return root.value;
    }
    public Node remove(Node node, E value){
        Node retNode = null;
        if(node == null)
            return retNode;
        if(value.compareTo(node.value) > 0){
            node.right = remove(node.right,value);
            retNode = node;
        }
        else if(value.compareTo(node.value) < 0){
            node.left = remove(node.left,value);
            retNode = node;
        }
        //value.compareTo(node.value) = 0
        else{
            //左右节点都为空，或者左节点为空
            if(node.left == null){
                size--;
                retNode = node.right;
            }
            //右节点为空
            else if(node.right == null){
                size--;
                retNode = node.left;
            }
            //左右节点都不为空
            else{
                Node successor = new Node();
                //寻找右子树最小的节点
                Node cur = node.right;
                while(cur.left != null){
                    cur = cur.left;
                }
                successor.value  = cur.value;
                successor.right = remove(node.right,value);
                successor.left = node.left;
                node.left =  node.right = null;
                retNode = successor;
            }
            if(retNode == null)
                return null;
            //维护二叉树平衡
            //跟新height
            retNode.height = Math.max(getHeight(retNode.left),getHeight(retNode.right));
        }
        int balanceFactor = getBalanceFactor(retNode);
        //该子树不平衡且新插入节点(导致不平衡的节点)在左子树的左子树上，此时需要进行右旋
        if (balanceFactor > 1 && getBalanceFactor(retNode.left) >= 0) {
            return rightRotate(retNode);
        }
        //该子树不平衡且新插入节点(导致不平衡的节点)在右子树子树的右子树上，此时需要进行左旋
        else if (balanceFactor < -1 && getBalanceFactor(retNode.right) <= 0) {
            return leftRotate(retNode);
        }
        //该子树不平衡且新插入节点(导致不平衡的节点)在左子树的右子树上，此时需要先对左子树左旋，在整个树右旋
        else if (balanceFactor > 1 && getBalanceFactor(retNode.left) < 0) {
            retNode.left = leftRotate(retNode.left);
            return rightRotate(retNode);
        }
        //该子树不平衡且新插入节点(导致不平衡的节点)在右子树的左子树上，此时需要先对右子树右旋，再整个树左旋
        else if(balanceFactor < -1 && getBalanceFactor(retNode.right) > 0) {
            retNode.right = rightRotate(retNode.right);
            return leftRotate(retNode);
        }
        return  retNode;
    }

到此这篇关于Java深入分析了解平衡二叉树的文章就介绍到这了,更多相关Java平衡二叉树内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！