python数据结构算法分析

目录

• 1.算法分析的定义
• 2. 大O记法
• 3. 不同算法的大O记法
• 3.1 清点法
• 3.2 排序法
• 3.3 蛮力法
• 3.4 计数法
• 4. 列表和字典操作的复杂度
• 4.1 列表
• 4.2 字典

前文学习：

python数据类型: python数据结构：数据类型.
python的输入输出: python数据结构输入输出及控制和异常.
python面向对象: python数据结构面向对象.

今天我们来学习的内容是面试题中都避免不小了的问题，就是算法分析了，什么是算法分析，算法分析是用来分析一个算法的好坏的，大家完成一件事情写不一样的算法，就需要算法分析来评判算法的好坏，最常见的就是程序的复杂的O(n)。

1.算法分析的定义

有这样一个问题：当两个看上去不同的程序 解决同一个问题时，会有优劣之分么？答案是肯定的。算法分析关心的是基于所使用的计算资源比较算法。我们说甲算法比乙算法好，依据是甲算法有更高的资源利用率或使用更少的资源。从这个角度来看，上面两个函数其实差不多，它们本质上都利用同一个算法解决累加问题。

计算资源究竟指什么？思考这个问题很重要。有两种思考方式。

• 一是考虑算法在解决问题时 要占用的空间或内存。解决方案所需的空间总量一般由问题实例本身决定，但算法往往也会有特定的空间需求。
• 二是根据算法执行所需的时间进行分析和比较。这个指标有时称作算法的执行 时间或运行时间。要 衡 量 sumOfN 函数的执行时间，一个方法就是做基准分析。也就是说，我们会记录程序计算出结果所消耗的实际时间。在 Python 中，我们记录下函数就所处系统而言的开始时间和结束时间。time 模块中有一个 time 函数，它会以秒为单位返回自指定时间点起到当前的系统时钟时间。在首尾各调用一次这个函数，计算差值，就可以得到以秒为单位的执行时间。

举个例子：我们需要求解前n个数之和，通过计算所需时间来评判效率好坏。(这里使用time函数,并计算5次来看看大致需要多少时间)

第一种方法：循环方案

import time
def sumOfN2(n):
        start=time.time()
        thesum=0
        for i in range(1,n+1):
            thesum=thesum+i
        end=time.time()
        return thesum,end-start
#循环5次
for i in range(5):
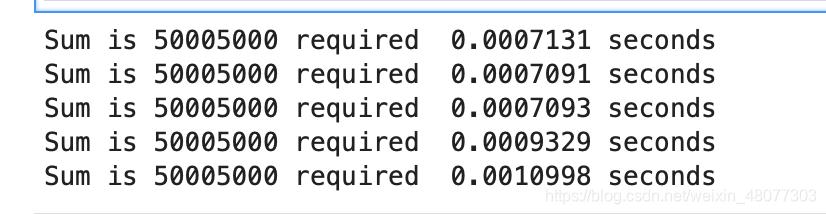
     print("Sum is %d required %10.7f seconds" % sumOfN2(10000))

结果如下：

第二种方法：公式方法

#直接利用求和公式
def sumOfN3(n):
        start=time.time()
        thesum=(1+n)*n/2
        end=time.time()
        return thesum,end-start
for i in range(5):
     print("Sum is %d required %10.7f seconds" % sumOfN3(10000))

结果如下：

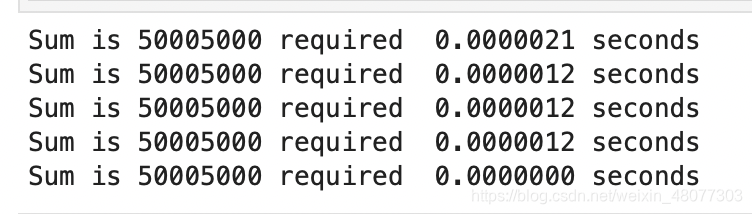
直觉上，循环方案看上去工作量更大，因为有些步骤重复。这好像是耗时更久的原因。而且，循环方案的耗时会随着 n 一起增长。然而，这里有个问题。如果在另一台计算机上运行这个函数，或用另一种编程语言来实现，很可能会得到不同的结果。如果计算机再旧些，sumOfN3 的执行时间甚至更长。
我们需要更好的方式来描述算法的执行时间。基准测试计算的是执行算法的实际时间。 这不是一个有用的指标，因为它依赖于特定的计算机、程序、时间、编译器与编程语言。我们希 望找到一个独立于程序或计算机的指标。这样的指标在评价算法方面会更有用，可以用来比较不同实现下的算法。

2. 大O记法

这里为了让大家知道一些函数的增长速度，我决定将一些函数的列举出来。

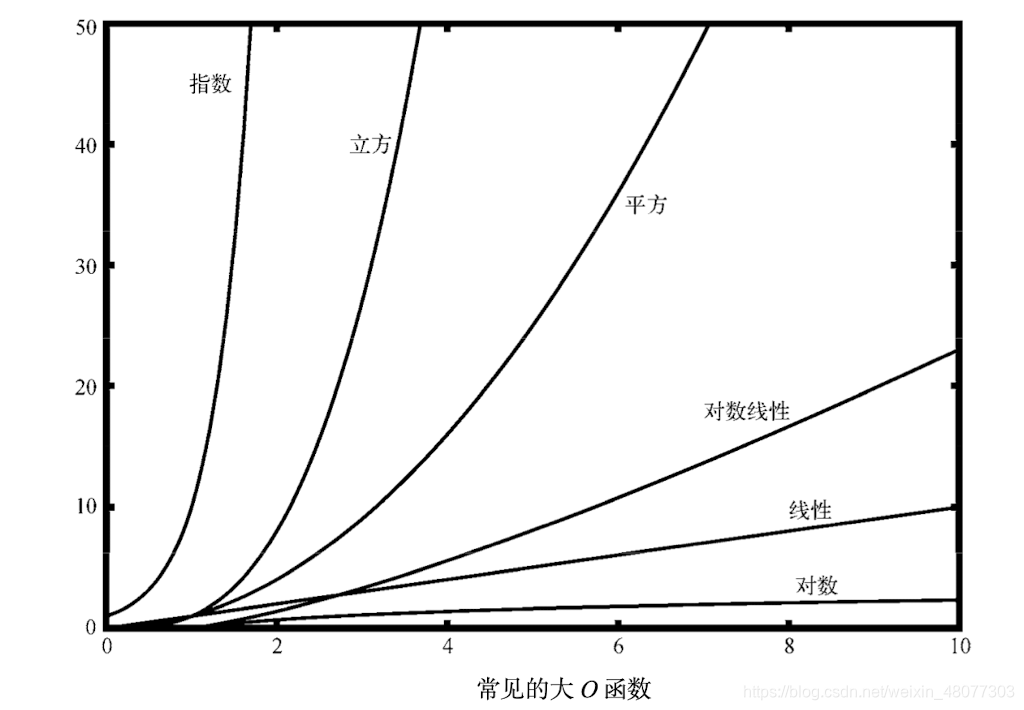
例：计算如下程序的步骤数，和数量级大O

a = 5
b = 6
c = 10
for i in range(n):
    for j in range(n):
        x = i * i
        y = j * j
        z = i * j
for k in range(n):
    w = a * k + 45
    v = b * b
d = 33

这段程序的赋值次数为：

大家可以自己算一下。

3. 不同算法的大O记法

这里我们采用不同的算法实现一个经典的异序词检测问，所谓异序词，就是组成单词的字母一样，只是顺序不同，例如heart和earth，python和typhon。为了简化问题，我们假设要检验的两个单词字符串的长度已经一样长。

3.1 清点法

该方法主要是清点第 1 个字符串的每个字符，看看它们是否都出现在第 2 个字符串中。如果是，那么两个字符串必然是异序词。清点是通过用 Python 中的特殊值 None 取代字符来实现的。但是，因为 Python 中的字符串是不可修改的，所以先要将第 2 个字符串转换成列表。在字符列表中检查第 1 个字符串中的每个字符，如果找到了，就替换掉。

def anagramSolution1(s1, s2):
    alist = list(s2)
    pos1=0
    stillOK = True
    while pos1 < len(s1) and stillOK:
          pos2 = 0
          found = False
          while pos2 < len(alist) and not found:
                if s1[pos1] == alist[pos2]:
                   found = True
                else:
                   pos2 = pos2 + 1
          if found:
                alist[pos2] = None
          else:
                stillOK = False
          pos1 = pos1 + 1
    return stillOK

来分析这个算法。注意，对于 s1 中的 n 个字符，检查每一个时都要遍历 s2 中的 n 个字符。 要匹配 s1 中的一个字符，列表中的 n 个位置都要被访问一次。因此，访问次数就成了从 1 到 n 的整数之和。这可以用以下公式来表示。

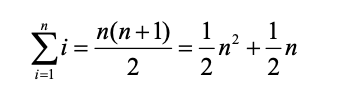
因此，该方法的时间复杂度是

3.2 排序法

尽管 s1 与 s2 是不同的字符串，但只要由相同的字符构成，它们就是异序词。基于这一点， 可以采用另一个方案。如果按照字母表顺序给字符排序，异序词得到的结果将是同一个字符串。

def anagramSolution2(s1, s2):
       alist1 = list(s1)
       alist2 = list(s2)
       alist1.sort()
       alist2.sort()
       pos=0
       matches = True
       while pos < len(s1) and matches:
             if alist1[pos] == alist2[pos]:
                pos = pos + 1
             else:
                matches = False
      return matches

乍看之下，你可能会认为这个算法的时间复杂度是O ( n ) O(n)O(n)，因为在排序之后只需要遍历一次就可以比较 n 个字符。但是，调用两次 sort 方法不是没有代价。我们在后面会看到，排序的时 间复杂度基本上是O ( n 2 ) O(n2 )O(n2)或 O ( n l o g n ) O(nlogn)O(nlogn) ，所以排序操作起主导作用。也就是说，该算法和排序过程的数量级相同。

3.3 蛮力法

用蛮力解决问题的方法基本上就是穷尽所有的可能。就异序词检测问题而言，可以用 s1 中 的字符生成所有可能的字符串，看看 s2 是否在其中。但这个方法有个难处。用 s1 中的字符生 成所有可能的字符串时，第 1 个字符有 n 种可能，第 2 个字符有 n-1 种可能，第 3 个字符有 n-2 种可能，依此类推。字符串的总数是n ∗ ( n − 1 ) ∗ ( n − 2 ) ∗ . . . . . . ∗ 3 ∗ 2 ∗ 1 n*(n-1)*(n-2)*......*3*2*1n∗(n−1)∗(n−2)∗......∗3∗2∗1,即为n ! n!n!也许有些字符串会重复，但程序无法预见，所以肯定会生成n ! n!n!个字符串。
当 n 较大时， n! 增长得比2n还要快。实际上，如果 s1 有20个字符，那么字符串的个数就 是 20!= 2432902008176640000 。假设每秒处理一个，处理完整个列表要花 77146816596 年。 这可不是个好方案。

3.4 计数法

最后一个方案基于这样一个事实:两个异序词有同样数目的 a、同样数目的 b、同样数目的 c，等等。要判断两个字符串是否为异序词，先数一下每个字符出现的次数。因为字符可能有 26 种，所以使用 26 个计数器，对应每个字符。每遇到一个字符，就将对应的计数器加 1。最后， 如果两个计数器列表相同，那么两个字符串肯定是异序词。

def anagramSolution4(s1, s2):
       c1=[0]*26
       c2=[0]*26

       for i in range(len(s1)):
           pos = ord(s1[i]) - ord('a')
           c1[pos] = c1[pos] + 1

       for i in range(len(s2)):
          pos = ord(s2[i]) - ord('a')
          c2[pos] = c2[pos] + 1
       j=0
       stillOK = True
       while j < 26 and stillOK:
             if c1[j] == c2[j]:
                j=j+1
             else:
                stillOK = False
       return stillOK

这个方案也有循环。但不同于方案 1，这个方案的循环没有嵌套。前两个计数循环都是 n 阶 的。第 3 个循环比较两个列表，由于可能有 26 种字符，因此会循环 26 次。全部加起来，得到总步骤数 T (n) =2n - 26 ，即 O(n) 。我们找到了解决异序词检测问题的线性阶算法。

4. 列表和字典操作的复杂度

4.1 列表

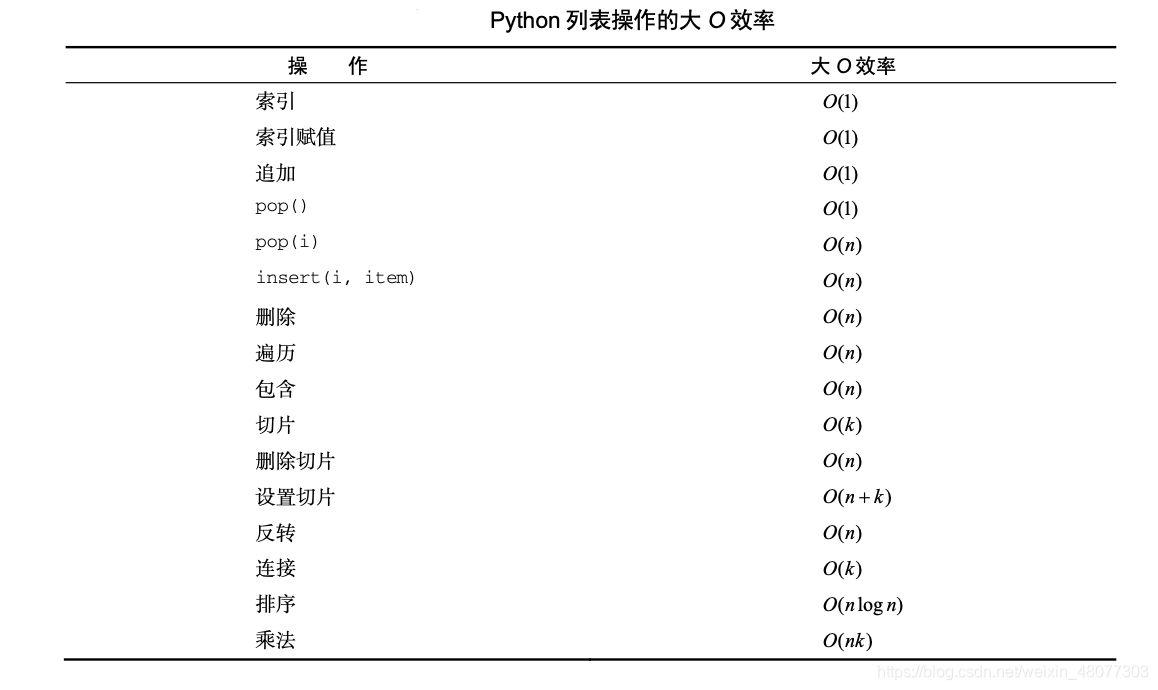
4.2 字典

到此这篇关于python数据结构算法分析的文章就介绍到这了,更多相关python 算法分析内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！