Java 数据结构与算法系列精讲之排序算法
概述
从今天开始, 小白我将带大家开启 Java 数据结构 & 算法的新篇章.

冒泡排序
冒泡排序 (Bubble Sort) 是一种简单的排序算法. 它重复地遍历要排序的数列, 一次比较两个元素, 如果他们的顺序错误就把他们交换过来. 遍历数列的工作是重复地进行直到没有再需要交换, 也就是说该数列已经排序完成. 这个算法的名字由来是因为越小的元素会经由交换慢慢 “浮” 到数列的顶端.

冒泡排序流程:
- 通过比较相邻的元素, 判断两个元素位置是否需要互换
- 进行 n-1 次比较, 结尾的元素就会是最大元素
- 重复以上冒泡过程 n 次
代码实现:
import java.util.Arrays;
public class bubble {
public static void main(String[] args) {
// 创建数据
int[] array = {426,375474,8465,453};
// 实现排序
System.out.println(Arrays.toString(array));
System.out.println(Arrays.toString(bubbleSort(array)));
}
public static int[] bubbleSort(int[] array) {
// 如果数组为空, 返回
if (array.length == 0){
return array;
}
// 执行冒泡过程n次, n为数组长度
for (int i = 0; i < array.length; i++) {
// 冒泡过程
for (int j = 0; j < array.length - 1 - i; j++) {
// 判断j索引的元素是否比j+1索引的元素大
if (array[j+1] < array[j]) {
// 交换位置
int temp = array[j + 1];
array[j + 1] = array[j];
array[j] = temp;
}
}
}
return array;
}
}
输出结果:
[426, 375474, 8465, 453]
[426, 453, 8465, 375474]
插入排序
插入排序 (Insertion Sort) 是一种简单直观的排序算法. 它的工作原理是通过构建有序序列, 对于未排序数据, 在已排序序列中从后向前扫描,找到相应位置并插入. 插入排序在实现上, 在从后向前扫描过程中, 需要反复把已排序元素逐步向后挪位, 为最新元素提供插入空间.

插入排序流程:
- 从第二个元素开始, 从后往前扫描
- 逐个比较元素大小, 之道插入到合适的位置
- 重复以上步骤 n-1 次
代码实现:
import java.util.Arrays;
public class insert {
public static void main(String[] args) {
// 创建数据
int[] array = {426,375474,8465,453};
// 实现排序
System.out.println(Arrays.toString(array));
System.out.println(Arrays.toString(insertionSort(array)));
}
public static int[] insertionSort(int[] array) {
// 如果数组为空, 返回
if (array.length == 0)
return array;
// 待排序元素
int current;
// 执行插入过程n-1次
for (int i = 0; i < array.length - 1; i++) {
// 指定待排序元素
current = array[i + 1];
int preIndex = i;
// 执行插入过程, 往前一个个比对
while (preIndex >= 0 && current < array[preIndex]) {
array[preIndex + 1] = array[preIndex];
preIndex--;
}
// 插入元素
array[preIndex + 1] = current;
}
return array;
}
}
输出结果:
[426, 375474, 8465, 453]
[426, 453, 8465, 375474]
归并排序
归并排序 (Merge Sort) 是一种建立在归并操作上的算法, 是分治的一个经典应用.
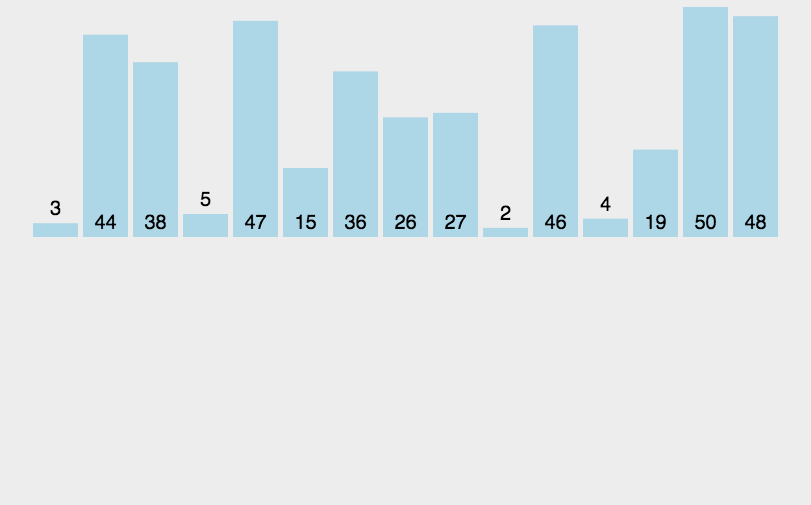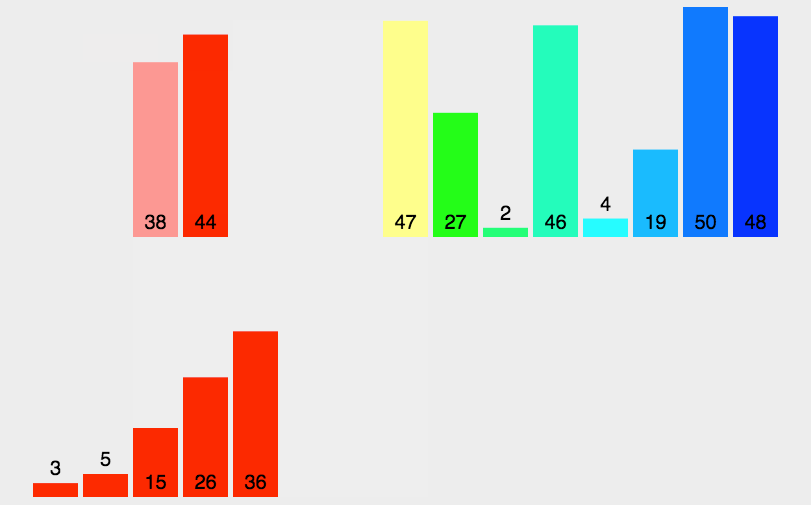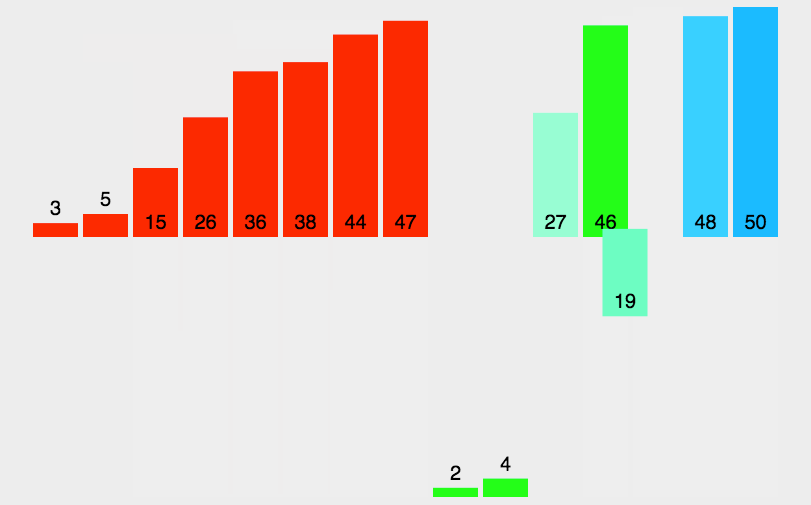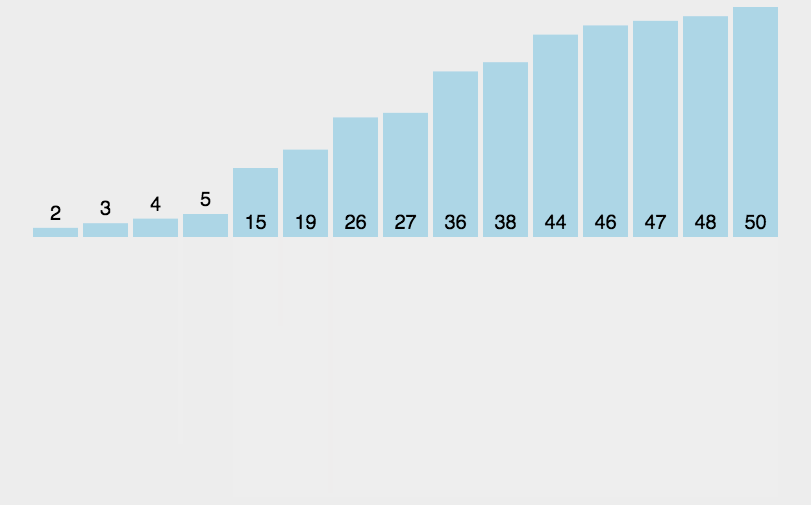
归并排序流程:
- 把数组拆分成两个 n/2 长度的子序列
- 对这两个子序列分别采用归并排序
- 将排序好的序列合并成最终序列
代码实现:
import java.util.Arrays;
public class merge {
public static void main(String[] args) {
// 创建数据
int[] array = {426,375474,8465,453};
// 实现排序
System.out.println(Arrays.toString(array));
System.out.println(Arrays.toString(mergeSort(array)));
}
public static int[] mergeSort(int[] array) {
// 如果数组长度小于2, 返回
if (array.length < 2) {
return array;
}
// 分治
int mid = array.length / 2;
int[] left = Arrays.copyOfRange(array, 0, mid);
int[] right = Arrays.copyOfRange(array, mid, array.length);
return merge(mergeSort(left), mergeSort(right));
}
public static int[] merge(int[] left, int[] right) {
// 创建数组用于存放合并后的序列
int[] result = new int[left.length + right.length];
for (int index = 0, i = 0, j = 0; index < result.length; index++) {
// 左序列取完
if (i >= left.length)
result[index] = right[j++];
// 右序列取完
else if (j >= right.length)
result[index] = left[i++];
// 左序列的第i个大于有序列的第j个
else if (left[i] > right[j])
result[index] = right[j++];
else
result[index] = left[i++];
}
return result;
}
}
输出结果:
[426, 375474, 8465, 453]
[426, 453, 8465, 375474]
快速排序
快速排序 (Quicksort) 通过一趟排序将要排序的数据分割成独立的两部分, 其中一部分的所有数据都比另外一部分的所有数据都要小, 然后再按此方法对这两部分数据分别进行快速排序, 整个排序过程可以递归进行, 以此达到整个数据变成有序序列.

快速排序流程:
- 从数组中挑出一个元素作为基准 (Pivot), 通常为第一个或者最后一个元素将比基准元素
- 小的值放到基准前面, 比基准元素大的值放到基准后面
- 递归进行分区操作
代码实现:
import java.util.Arrays;
public class quick {
public static void main(String[] args) {
// 创建数据
int[] array = {426, 375474, 8465, 453};
// 实现排序
System.out.println(Arrays.toString(array));
quickSort(array, 0, array.length - 1);
System.out.println(Arrays.toString(array));
}
public static void quickSort(int[] arr, int low, int high) {
// 定义
int p, i, j, temp;
if (low >= high) {
return;
}
// p就是基准数, 每个数组的第一个
p = arr[low];
i = low;
j = high;
while (i < j) {
//右边当发现小于p的值时停止循环
while (arr[j] >= p && i < j) {
j--;
}
//这里一定是右边开始,上下这两个循环不能调换(下面有解析,可以先想想)
//左边当发现大于p的值时停止循环
while (arr[i] <= p && i < j) {
i++;
}
temp = arr[j];
arr[j] = arr[i];
arr[i] = temp;
}
// 交换p和arr[i]
arr[low] = arr[i];
arr[i] = p;
// 分别进行快排
quickSort(arr, low, j - 1);
quickSort(arr, j + 1, high);
}
}
输出结果:
[426, 375474, 8465, 453]
[426, 453, 8465, 375474]
总结
| 算法 | 时间复杂度 | 稳定性 | 适用场景 |
|---|---|---|---|
| 冒泡排序 | O ( n 2 ) O(n^2) O(n2) | 稳定 | 数组大致为从小到大 |
| 插入排序 | O ( n 2 ) O(n^2) O(n2) | 稳定 | 适用于数组较小的场景 |
| 归并排序 | O ( n l o g n ) O(nlogn) O(nlogn) | 稳定 | 适用于数组较大的场景 |
| 快速排序 | O ( n l o g n ) O(nlogn) O(nlogn) | 不稳定 | 适用于数组较大的场景 |
到此这篇关于Java 数据结构与算法系列精讲之排序算法的文章就介绍到这了,更多相关Java 排序算法内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们!

