带你了解Java数据结构和算法之链表

目录

• 1、链表（Linked List）
• 2、单向链表（Single-Linked List）
• ①、单向链表的具体实现
• ②、用单向链表实现栈
• 4、双端链表
• ①、双端链表的具体实现
• ②、用双端链表实现队列
• 5、抽象数据类型（ADT）
• 6、有序链表
• 7、有序链表和无序数组组合排序
• 8、双向链表
• 9、总结

前面博客我们在讲解数组中，知道数组作为数据存储结构有一定的缺陷。在无序数组中，搜索性能差，在有序数组中，插入效率又很低，而且这两种数组的删除效率都很低，并且数组在创建后，其大小是固定了，设置的过大会造成内存的浪费，过小又不能满足数据量的存储。

本篇博客我们将讲解一种新型的数据结构——链表。我们知道数组是一种通用的数据结构，能用来实现栈、队列等很多数据结构。而链表也是一种使用广泛的通用数据结构，它也可以用来作为实现栈、队列等数据结构的基础，基本上除非需要频繁的通过下标来随机访问各个数据，否则很多使用数组的地方都可以用链表来代替。

但是我们需要说明的是，链表是不能解决数据存储的所有问题的，它也有它的优点和缺点。本篇博客我们介绍几种常见的链表，分别是单向链表、双端链表、有序链表、双向链表以及有迭代器的链表。并且会讲解一下抽象数据类型（ADT）的思想，如何用 ADT 描述栈和队列，如何用链表代替数组来实现栈和队列。

1、链表（Linked List）

链表通常由一连串节点组成，每个节点包含任意的实例数据（data fields）和一或两个用来指向上一个/或下一个节点的位置的链接（"links"）

链表（Linked list）是一种常见的基础数据结构，是一种线性表，但是并不会按线性的顺序存储数据，而是在每一个节点里存到下一个节点的指针(Pointer)。

使用链表结构可以克服数组链表需要预先知道数据大小的缺点，链表结构可以充分利用计算机内存空间，实现灵活的内存动态管理。但是链表失去了数组随机读取的优点，同时链表由于增加了结点的指针域，空间开销比较大。

2、单向链表（Single-Linked List）

单链表是链表中结构最简单的。一个单链表的节点(Node)分为两个部分，第一个部分(data)保存或者显示关于节点的信息，另一个部分存储下一个节点的地址。最后一个节点存储地址的部分指向空值。

单向链表只可向一个方向遍历，一般查找一个节点的时候需要从第一个节点开始每次访问下一个节点，一直访问到需要的位置。而插入一个节点，对于单向链表，我们只提供在链表头插入，只需要将当前插入的节点设置为头节点，next指向原头节点即可。删除一个节点，我们将该节点的上一个节点的next指向该节点的下一个节点。　　

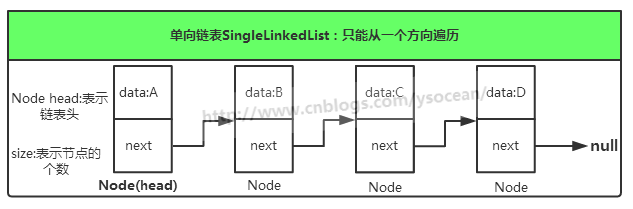
在表头增加节点：

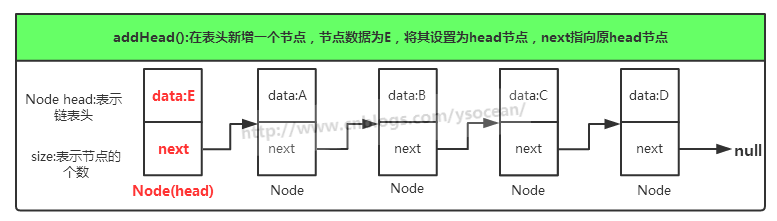
删除节点：　　

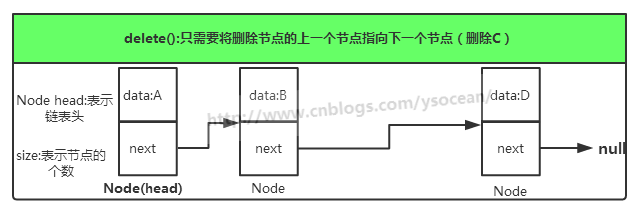
①、单向链表的具体实现

package com.ys.datastructure;
public class SingleLinkedList {
    private int size;//链表节点的个数
    private Node head;//头节点
    public SingleLinkedList(){
        size = 0;
        head = null;
    }
    //链表的每个节点类
    private class Node{
        private Object data;//每个节点的数据
        private Node next;//每个节点指向下一个节点的连接
        public Node(Object data){
            this.data = data;
        }
    }
    //在链表头添加元素
    public Object addHead(Object obj){
        Node newHead = new Node(obj);
        if(size == 0){
            head = newHead;
        }else{
            newHead.next = head;
            head = newHead;
        }
        size++;
        return obj;
    }
    //在链表头删除元素
    public Object deleteHead(){
        Object obj = head.data;
        head = head.next;
        size--;
        return obj;
    }
    //查找指定元素，找到了返回节点Node，找不到返回null
    public Node find(Object obj){
        Node current = head;
        int tempSize = size;
        while(tempSize > 0){
            if(obj.equals(current.data)){
                return current;
            }else{
                current = current.next;
            }
            tempSize--;
        }
        return null;
    }
    //删除指定的元素，删除成功返回true
    public boolean delete(Object value){
        if(size == 0){
            return false;
        }
        Node current = head;
        Node previous = head;
        while(current.data != value){
            if(current.next == null){
                return false;
            }else{
                previous = current;
                current = current.next;
            }
        }
        //如果删除的节点是第一个节点
        if(current == head){
            head = current.next;
            size--;
        }else{//删除的节点不是第一个节点
            previous.next = current.next;
            size--;
        }
        return true;
    }
    //判断链表是否为空
    public boolean isEmpty(){
        return (size == 0);
    }
    //显示节点信息
    public void display(){
        if(size >0){
            Node node = head;
            int tempSize = size;
            if(tempSize == 1){//当前链表只有一个节点
                System.out.println("["+node.data+"]");
                return;
            }
            while(tempSize>0){
                if(node.equals(head)){
                    System.out.print("["+node.data+"->");
                }else if(node.next == null){
                    System.out.print(node.data+"]");
                }else{
                    System.out.print(node.data+"->");
                }
                node = node.next;
                tempSize--;
            }
            System.out.println();
        }else{//如果链表一个节点都没有，直接打印[]
            System.out.println("[]");
        }
    }
}

测试：

@Test
public void testSingleLinkedList(){
    SingleLinkedList singleList = new SingleLinkedList();
    singleList.addHead("A");
    singleList.addHead("B");
    singleList.addHead("C");
    singleList.addHead("D");
    //打印当前链表信息
    singleList.display();
    //删除C
    singleList.delete("C");
    singleList.display();
    //查找B
    System.out.println(singleList.find("B"));
}

打印结果：

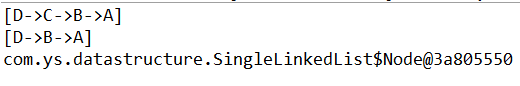
②、用单向链表实现栈

栈的pop()方法和push()方法，对应于链表的在头部删除元素deleteHead()以及在头部增加元素addHead()。

package com.ys.datastructure;
public class StackSingleLink {
    private SingleLinkedList link;
    public StackSingleLink(){
        link = new SingleLinkedList();
    }
    //添加元素
    public void push(Object obj){
        link.addHead(obj);
    }
    //移除栈顶元素
    public Object pop(){
        Object obj = link.deleteHead();
        return obj;
    }
    //判断是否为空
    public boolean isEmpty(){
        return link.isEmpty();
    }
    //打印栈内元素信息
    public void display(){
        link.display();
    }
}

4、双端链表

对于单项链表，我们如果想在尾部添加一个节点，那么必须从头部一直遍历到尾部，找到尾节点，然后在尾节点后面插入一个节点。这样操作很麻烦，如果我们在设计链表的时候多个对尾节点的引用，那么会简单很多。　　

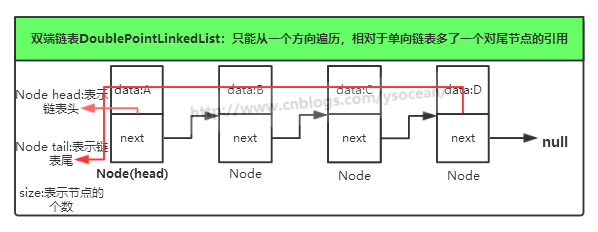
注意和后面将的双向链表的区别！！！

①、双端链表的具体实现

package com.ys.link;
public class DoublePointLinkedList {
    private Node head;//头节点
    private Node tail;//尾节点
    private int size;//节点的个数
    private class Node{
        private Object data;
        private Node next;
        public Node(Object data){
            this.data = data;
        }
    }
    public DoublePointLinkedList(){
        size = 0;
        head = null;
        tail = null;
    }
    //链表头新增节点
    public void addHead(Object data){
        Node node = new Node(data);
        if(size == 0){//如果链表为空，那么头节点和尾节点都是该新增节点
            head = node;
            tail = node;
            size++;
        }else{
            node.next = head;
            head = node;
            size++;
        }
    }
    //链表尾新增节点
    public void addTail(Object data){
        Node node = new Node(data);
        if(size == 0){//如果链表为空，那么头节点和尾节点都是该新增节点
            head = node;
            tail = node;
            size++;
        }else{
            tail.next = node;
            tail = node;
            size++;
        }
    }
    //删除头部节点，成功返回true，失败返回false
    public boolean deleteHead(){
        if(size == 0){//当前链表节点数为0
            return false;
        }
        if(head.next == null){//当前链表节点数为1
            head = null;
            tail = null;
        }else{
            head = head.next;
        }
        size--;
        return true;
    }
    //判断是否为空
    public boolean isEmpty(){
        return (size ==0);
    }
    //获得链表的节点个数
    public int getSize(){
        return size;
    }
    //显示节点信息
    public void display(){
        if(size >0){
            Node node = head;
            int tempSize = size;
            if(tempSize == 1){//当前链表只有一个节点
                System.out.println("["+node.data+"]");
                return;
            }
            while(tempSize>0){
                if(node.equals(head)){
                    System.out.print("["+node.data+"->");
                }else if(node.next == null){
                    System.out.print(node.data+"]");
                }else{
                    System.out.print(node.data+"->");
                }
                node = node.next;
                tempSize--;
            }
            System.out.println();
        }else{//如果链表一个节点都没有，直接打印[]
            System.out.println("[]");
        }
    }
}

②、用双端链表实现队列

package com.ys.link;
public class QueueLinkedList {
    private DoublePointLinkedList dp;
    public QueueLinkedList(){
        dp = new DoublePointLinkedList();
    }
    public void insert(Object data){
        dp.addTail(data);
    }
    public void delete(){
        dp.deleteHead();
    }
    public boolean isEmpty(){
        return dp.isEmpty();
    }
    public int getSize(){
        return dp.getSize();
    }
    public void display(){
        dp.display();
    }
}

5、抽象数据类型（ADT）

在介绍抽象数据类型的时候，我们先看看什么是数据类型，听到这个词，在Java中我们可能首先会想到像 int,double这样的词，这是Java中的基本数据类型，一个数据类型会涉及到两件事：

• ①、拥有特定特征的数据项
• ②、在数据上允许的操作

比如Java中的int数据类型，它表示整数，取值范围为：-2147483648~2147483647，还能使用各种操作符，+、-、*、/ 等对其操作。数据类型允许的操作是它本身不可分离的部分，理解类型包括理解什么样的操作可以应用在该类型上。

那么当年设计计算机语言的人，为什么会考虑到数据类型？

我们先看这样一个例子，比如，大家都需要住房子，也都希望房子越大越好。但显然，没有钱，考虑房子没有意义。于是就出现了各种各样的商品房，有别墅的、复式的、错层的、单间的……甚至只有两平米的胶囊房间。这样做的意义是满足不同人的需要。

同样，在计算机中，也存在相同的问题。计算1+1这样的表达式不需要开辟很大的存储空间，不需要适合小数甚至字符运算的内存空间。于是计算机的研究者们就考虑，要对数据进行分类，分出来多种数据类型。比如int，比如float。

虽然不同的计算机有不同的硬件系统，但实际上高级语言编写者才不管程序运行在什么计算机上，他们的目的就是为了实现整形数字的运算，比如a+b等。他们才不关心整数在计算机内部是如何表示的，也不管CPU是如何计算的。于是我们就考虑，无论什么计算机、什么语言都会面临类似的整数运算，我们可以考虑将其抽象出来。抽象是抽取出事物具有的普遍性本质，是对事物的一个概括，是一种思考问题的方式。

抽象数据类型（ADT）是指一个数学模型及定义在该模型上的一组操作。它仅取决于其逻辑特征，而与计算机内部如何表示和实现无关。比如刚才说得整型，各个计算机，不管大型机、小型机、PC、平板电脑甚至智能手机，都有“整型”类型，也需要整形运算，那么整型其实就是一个抽象数据类型。　

更广泛一点的，比如我们刚讲解的栈和队列这两种数据结构，我们分别使用了数组和链表来实现，比如栈，对于使用者只需要知道pop()和push()方法或其它方法的存在以及如何使用即可，使用者不需要知道我们是使用的数组或是链表来实现的。

ADT的思想可以作为我们设计工具的理念，比如我们需要存储数据，那么就从考虑需要在数据上实现的操作开始，需要存取最后一个数据项吗？还是第一个？还是特定值的项？还是特定位置的项？回答这些问题会引出ADT的定义，只有完整的定义了ADT后，才应该考虑实现的细节。

这在我们Java语言中的接口设计理念是想通的。

6、有序链表

前面的链表实现插入数据都是无序的，在有些应用中需要链表中的数据有序，这称为有序链表。

在有序链表中，数据是按照关键值有序排列的。一般在大多数需要使用有序数组的场合也可以使用有序链表。有序链表优于有序数组的地方是插入的速度（因为元素不需要移动），另外链表可以扩展到全部有效的使用内存，而数组只能局限于一个固定的大小中。

package com.ys.datastructure;
public class OrderLinkedList {
    private Node head;
    private class Node{
        private int data;
        private Node next;
        public Node(int data){
            this.data = data;
        }
    }
    public OrderLinkedList(){
        head = null;
    }
    //插入节点，并按照从小打到的顺序排列
    public void insert(int value){
        Node node = new Node(value);
        Node pre = null;
        Node current = head;
        while(current != null && value > current.data){
            pre = current;
            current = current.next;
        }
        if(pre == null){
            head = node;
            head.next = current;
        }else{
            pre.next = node;
            node.next = current;
        }
    }
    //删除头节点
    public void deleteHead(){
        head = head.next;
    }
    public void display(){
        Node current = head;
        while(current != null){
            System.out.print(current.data+" ");
            current = current.next;
        }
        System.out.println("");
    }
}

在有序链表中插入和删除某一项最多需要O(N)次比较，平均需要O(N/2)次，因为必须沿着链表上一步一步走才能找到正确的插入位置，然而可以最快速度删除最值，因为只需要删除表头即可，如果一个应用需要频繁的存取最小值，且不需要快速的插入，那么有序链表是一个比较好的选择方案。比如优先级队列可以使用有序链表来实现。

7、有序链表和无序数组组合排序

比如有一个无序数组需要排序，前面我们在讲解冒泡排序、选择排序、插入排序这三种简单的排序时，需要的时间级别都是O(N2)。

现在我们讲解了有序链表之后，对于一个无序数组，我们先将数组元素取出，一个一个的插入到有序链表中，然后将他们从有序链表中一个一个删除，重新放入数组，那么数组就会排好序了。和插入排序一样，如果插入了N个新数据，那么进行大概N2/4次比较。但是相对于插入排序，每个元素只进行了两次排序，一次从数组到链表，一次从链表到数组，大概需要2*N次移动，而插入排序则需要N2次移动，

效率肯定是比前面讲的简单排序要高，但是缺点就是需要开辟差不多两倍的空间，而且数组和链表必须在内存中同时存在，如果有现成的链表可以用，那么这种方法还是挺好的。

8、双向链表

我们知道单向链表只能从一个方向遍历，那么双向链表它可以从两个方向遍历。

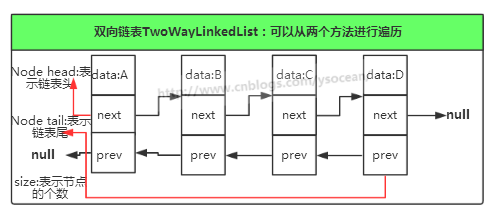
具体代码实现：

package com.ys.datastructure;
public class TwoWayLinkedList {
    private Node head;//表示链表头
    private Node tail;//表示链表尾
    private int size;//表示链表的节点个数
    private class Node{
        private Object data;
        private Node next;
        private Node prev;
        public Node(Object data){
            this.data = data;
        }
    }
    public TwoWayLinkedList(){
        size = 0;
        head = null;
        tail = null;
    }
    //在链表头增加节点
    public void addHead(Object value){
        Node newNode = new Node(value);
        if(size == 0){
            head = newNode;
            tail = newNode;
            size++;
        }else{
            head.prev = newNode;
            newNode.next = head;
            head = newNode;
            size++;
        }
    }
    //在链表尾增加节点
    public void addTail(Object value){
        Node newNode = new Node(value);
        if(size == 0){
            head = newNode;
            tail = newNode;
            size++;
        }else{
            newNode.prev = tail;
            tail.next = newNode;
            tail = newNode;
            size++;
        }
    }
    //删除链表头
    public Node deleteHead(){
        Node temp = head;
        if(size != 0){
            head = head.next;
            head.prev = null;
            size--;
        }
        return temp;
    }
    //删除链表尾
    public Node deleteTail(){
        Node temp = tail;
        if(size != 0){
            tail = tail.prev;
            tail.next = null;
            size--;
        }
        return temp;
    }
    //获得链表的节点个数
    public int getSize(){
        return size;
    }
    //判断链表是否为空
    public boolean isEmpty(){
        return (size == 0);
    }
    //显示节点信息
    public void display(){
        if(size >0){
            Node node = head;
            int tempSize = size;
            if(tempSize == 1){//当前链表只有一个节点
                System.out.println("["+node.data+"]");
                return;
            }
            while(tempSize>0){
                if(node.equals(head)){
                    System.out.print("["+node.data+"->");
                }else if(node.next == null){
                    System.out.print(node.data+"]");
                }else{
                    System.out.print(node.data+"->");
                }
                node = node.next;
                tempSize--;
            }
            System.out.println();
        }else{//如果链表一个节点都没有，直接打印[]
            System.out.println("[]");
        }
    }
}

我们也可以用双向链表来实现双端队列，这里就不做具体代码演示了。

9、总结

上面我们讲了各种链表，每个链表都包括一个LinikedList对象和许多Node对象，LinkedList对象通常包含头和尾节点的引用，分别指向链表的第一个节点和最后一个节点。而每个节点对象通常包含数据部分data，以及对上一个节点的引用prev和下一个节点的引用next，只有下一个节点的引用称为单向链表，两个都有的称为双向链表。next值为null则说明是链表的结尾，如果想找到某个节点，我们必须从第一个节点开始遍历，不断通过next找到下一个节点，直到找到所需要的。栈和队列都是ADT，可以用数组来实现，也可以用链表实现。

本篇文章就到这里了，希望能够给你带来帮助，也希望您能够多多关注我们的更多内容!