Python要求O(n)复杂度求无序列表中第K的大元素实例
昨天面试上来就是一个算法,平时基本的算法还行,结果变个法就不会了。。。感觉应该刷一波Leecode冷静下。。。今天抽空看下。
题目就是要求O(n)复杂度求无序列表中第K的大元素
如果没有复杂度的限制很简单。。。加了O(n)复杂度确实有点蒙
虽然当时面试官说思路对了,但是还是没搞出来,最后面试官提示用快排的思想
主要还是设立一个flag,列表中小于flag的组成左列表,大于等于flag的组成右列表,主要是不需要在对两侧列表在进行排序了,只需要生成左右列表就行,所以可以实现复杂度O(n)。
举个例子说明下步骤,比如有列表test_list=[6,5,4,3,2,1],找出第3大的元素,就是4,
如果flag=4:
l_list=[3,2,1]
r_list=[6,5]
因为第3大的元素,r_list长度为2,自然flag就是第3大的元素了,return flag,len(r_list)==k-1,就是结束递归的基线条件。
如果flag=1:
l_list=[]
r_list=[6,5,4,3,2]
问题就变成了求r_list里面第K大的元素了
如果flag=6:
l_list=[5,4,3,2,1]
r_list=[]
相当于求l_list里第k-(len(test_list)-len(r_list)+1)大的元素了,这里就是相当于求l_list=[5,4,3,2,1]第2大的元素
通过这三种情况进行递归,最终返回flag就是目标元素
最差复杂度就是n+n-1+n-2+n-3+......+1=(1+n)n/2,就是O(n²)
当时我就会回答出了最差复杂度肯定是n²啊,面试小哥说平均复杂度,我说计算平均复杂度好像很复杂吧?感觉他也有点蒙,就说每次都是二分的情况的复杂度,
当时竟然回答了个logn*logn。。。最后还是被面试管提示的。。。太尴尬了。。。
实际上如果每次刚好二分,第一次取flag比较次数是n,第二次是n/2,依次下去是n/4,n/8.....n/2
就是n+n/2+n/4....
最最丢人的是计算这个结果还想了一会。。。看样该做点高中上数学了。。。
实际结果自然是n(1+1/2+1/4+1/8+....1/2ⁿ)=2n,复杂度自然就是O(n)了
最后实现代码如下:
#给定一个无序列表,求出第K大的元素,要求复杂度O(n) def find_k(test_list,k): flag=test_list[0] test_list.pop(0) l_list=[i for i in test_list if i < flag] r_list=[i for i in test_list if i >= flag] #结果递归的基线条件 if len(r_list)==k-1: return flag elif len(r_list)>k-1: return find_k(r_list,k) else: #因为test_list.pop(0)让test_list少了一个元素,所以下面需要+1 gap=len(test_list)-len(l_list)+1 k=k-gap return find_k(l_list,k) if __name__ == '__main__': test_list = [5, 4, 3, 2, 1,10,20,100] res=find_k(test_list,1) print(res)
补充知识:从N个数选取k个数的组合--不降原则(DFS)
原理 :不降原则(看代码前先看一下原理吧)
举个例子:
比如说在6里面随便选5个数,那么选法都是什么呢?
瞎枚举?
12345
12346
前两个还不会弄混
然后很可能就乱了
少点数可能不会乱
但是多了就不好整了
比如说在100里随便选50个数。
1 2 3 4 5 6 7 8 9 10 11 12…
所以我们可以运用不降原则:
保证枚举的这些数是升序排列
其实真正的不降原则还可以平
比如 1 2 2 3 3 4…
但是这里要说的“不降原则”不能平哦!
对于这道题也不能平
否则就有重复数字了
拿6个里面选3个举例子
1 2 3
1 2 4
1 2 5
1 2 6
第一轮枚举完毕。
第二个数加一
1 3 ?
这个“?”应该是4,因为是升序排列
1 3 4
1 3 5
1 3 6
接着,就是这样
1 4 5
1 4 6
1 5 6
第一位是1枚举完毕
第一位是2呢?
2 3 4
2 3 5
2 3 6
2 4 5
2 4 6
2 5 6
就是这样的,枚举十分清晰,对吗?
以此类推…
3 4 5
3 4 6
3 5 6
4 5 6
然后就枚举不了了,结束。
所以说,这样就可以避免判重了。
代码
#include<iostream>
#include<cstring>
using namespace std;
int n,k; //全局变量:从n个数的集合中选取k个数
int a[25]; //存放n个数的集合数据
int vis[25];//在dfs中记录数据是否被访问过
int re[25];//存放被选取的数字
void dfs(int step,int start)//参数step代表选取第几个数字,参数start代表从集合的第几个开始选
{
if(step==k)//如果选够了k个就输出
{
for(int i=0;i<k;i++)
{
cout<<re[i]<<" ";
}
cout<<endl;
}
for(int i=start;i<n;i++)//不降原则的核心步骤1:从第i+1个开始选取数字(避免重选)
{
if(vis[i]==1)
continue;
vis[i]=1;
re[step]=a[i];
dfs(step+1,i+1); //不降原则的核心步骤2:从第i+1个开始选取数字(避免重选)
vis[i]=0;
}
return;
}
int main()
{
while(cin>>n>>k)
{
memset(a,0,sizeof(a));
memset(re,0,sizeof(re));
memset(vis,0,sizeof(vis));
for(int i=0;i<n;i++)
{
cin>>a[i];
}
dfs(0,0);
}
return 0;
}
运行结果
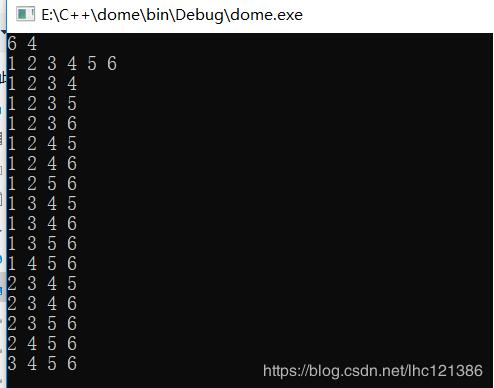
变形——从N个数中选取k个数求和(举一反三)
代码
#include<iostream>
#include<cstring>
using namespace std;
int n,k; //全局变量:从n个数的集合中选取k个数
int a[25]; //存放n个数的集合数据
int vis[25];//在dfs中记录数据是否被访问过
int re[25];//存放被选取的数字
void dfs(int step,int sum,int start)//参数step代表选取第几个数字,参数sum代表从选取前step-1个数时的总数,参数start代表从集合的第几个开始选
{
if(step==k)//如果选够了k个就输出
{
cout<<re[0];
for(int i=1;i<k;i++)
{
cout<<'+'<<re[i];
}
cout<<'='<<sum<<endl;
}
for(int i=start;i<n;i++)//不降原则的核心步骤1:从第i+1个开始选取数字(避免重选)
{
if(vis[i]==1)
continue;
vis[i]=1;
re[step]=a[i];
dfs(step+1,sum+a[i],i+1); //不降原则的核心步骤2:从第i+1个开始选取数字(避免重选)
vis[i]=0;
}
return;
}
int main()
{
while(cin>>n>>k)
{
memset(a,0,sizeof(a));
memset(re,0,sizeof(re));
memset(vis,0,sizeof(vis));
for(int i=0;i<n;i++)
{
cin>>a[i];
}
dfs(0,0,0);
}
return 0;
}
运行结果

变形——从N个数中选取k个数求积(举一反三)
代码
#include<iostream>
#include<cstring>
using namespace std;
int n,k; //全局变量:从n个数的集合中选取k个数
int a[25]; //存放n个数的集合数据
int vis[25];//在dfs中记录数据是否被访问过
int re[25];//存放被选取的数字
void dfs(int step,int sum,int start)//参数step代表选取第几个数字,参数start代表从集合的第几个开始选
{
if(step==k)//如果选够了k个就输出
{
cout<<re[0];
for(int i=1;i<k;i++)
{
cout<<'*'<<re[i];
}
cout<<'='<<sum<<endl;
}
for(int i=start;i<n;i++)//不降原则的核心步骤1:从第i+1个开始选取数字(避免重选)
{
if(vis[i]==1)
continue;
vis[i]=1;
re[step]=a[i];
dfs(step+1,sum*a[i],i+1); //不降原则的核心步骤2:从第i+1个开始选取数字(避免重选)
vis[i]=0;
}
return;
}
int main()
{
while(cin>>n>>k)
{
memset(a,0,sizeof(a));
memset(re,0,sizeof(re));
memset(vis,0,sizeof(vis));
for(int i=0;i<n;i++)
{
cin>>a[i];
}
dfs(0,1,0);
}
return 0;
}
运行结果

以上这篇Python要求O(n)复杂度求无序列表中第K的大元素实例就是小编分享给大家的全部内容了,希望能给大家一个参考,也希望大家多多支持我们。
