C语言数据结构中树与森林专项详解

目录

• 树的存储结构
• 树的逻辑结构
• 双亲表示法（顺序存储）
• 孩字表示法（顺序+链式存储）
• 孩子兄弟表示法（链式存储）
• 森林
• 树的遍历
• 树的先根遍历（深度优先遍历）
• 树的后根遍历（树的深度优先遍历）
• 树的层序遍历（广度优先遍历）
• 森林的遍历
• 先序遍历森林
• 中序遍历森林

树的存储结构

树的逻辑结构

树是n(n≥0)个结点的有限集合，n=0时，称为空树，这是一种特殊情况。在任意--棵非空树中应满足:

1)有且仅有一个特定的称为根的结点。

2)当n>1时，其余结点可分为m(m>0)个互不相交的有限集合T1,2....Tm，其中每个集合本身又是一-棵树，并且称为根结点的子树。

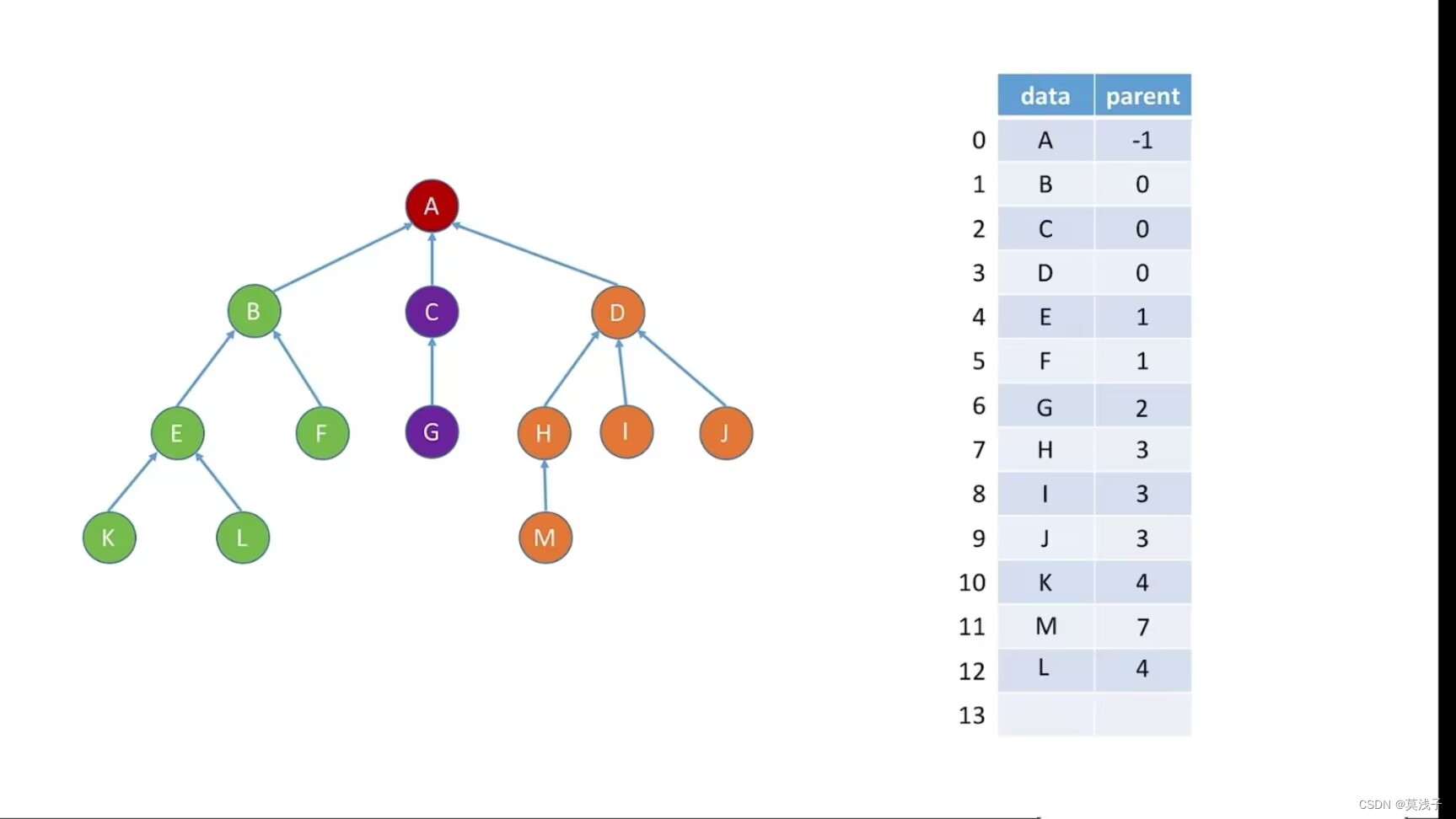
双亲表示法（顺序存储）

每个结点保存双亲的“指针”， 结点中保存父节点在数组的下标

优点：找父节点方便

缺点：找孩子不方便

删除元素方案一 ，数据删除后，parent 变为-1

删除元素方案二，数据删除后，将尾部数据填充到那

#define MAX_TREE_SIZE 100    //树中最多结点树
typedef struct{             //树的结点定义
	Elemtype date;         //数据元素
	int parent;           //双亲位置域
}PTNode;
typedef struct{                    //树的类型定义
	PTNode nodes[MAX_TREE_SIZE];   //双亲表示
	int n;                        //结点树
}PTree; 

孩字表示法（顺序+链式存储）

顺序存储各个结点，每个结点保存孩子链表头指针

优点：找孩子方便

缺点：找双亲不方便

代码

#define MAX_TREE_SIZE 100    //树中最多结点树
typedef struct{             //树的结点定义
	Elemtype date;         //数据元素
	int parent;           //双亲位置域
}PTNode;
typedef struct{                    //树的类型定义
	PTNode nodes[MAX_TREE_SIZE];   //双亲表示
	int n;                        //结点树
}PTree;
struct CTNOde{
	int child; //孩子结点在数组的位置
	struct CTNode *next;   //下一个孩子
}CTBox;
typedef struct {
	CTBox nodes[MAX_TREE_SIZE];
	int n,r;   //结点树和根的位置
}; 

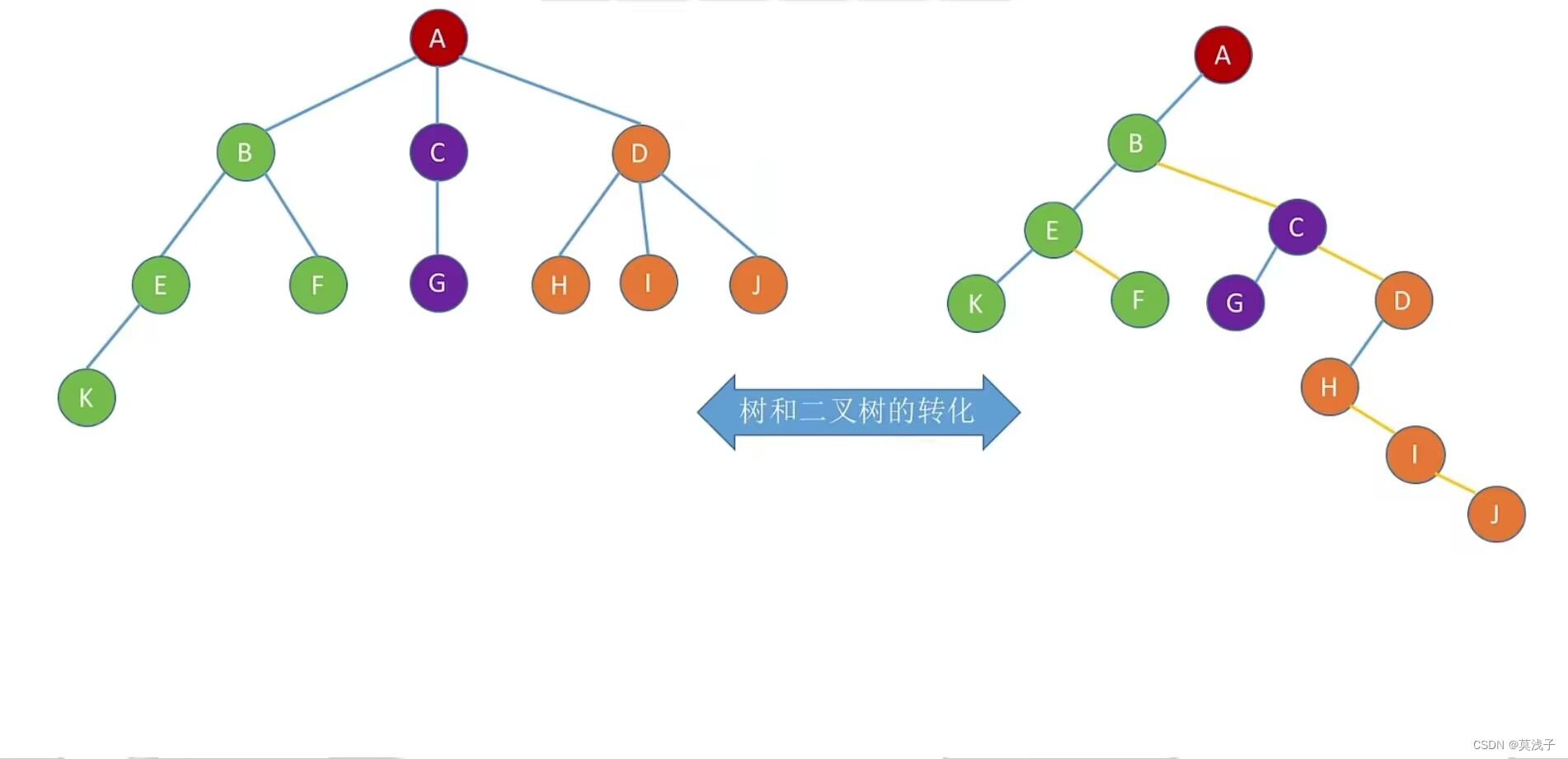
孩子兄弟表示法（链式存储）

优点：可以用二叉树的操作来处理树

代码

//树的存储-孩子兄弟表示法
typedef struct CSDode{
	Elemtype date;                    //数据域
	struct CSDode *firstchild ,*nextsibling;  //第一个孩子和右兄弟指针
}CSDode ,*CSTree; 

森林

森林是m（m>=0）棵互不相交的树集合

森林中各个树的根结点之间是为兄弟关系

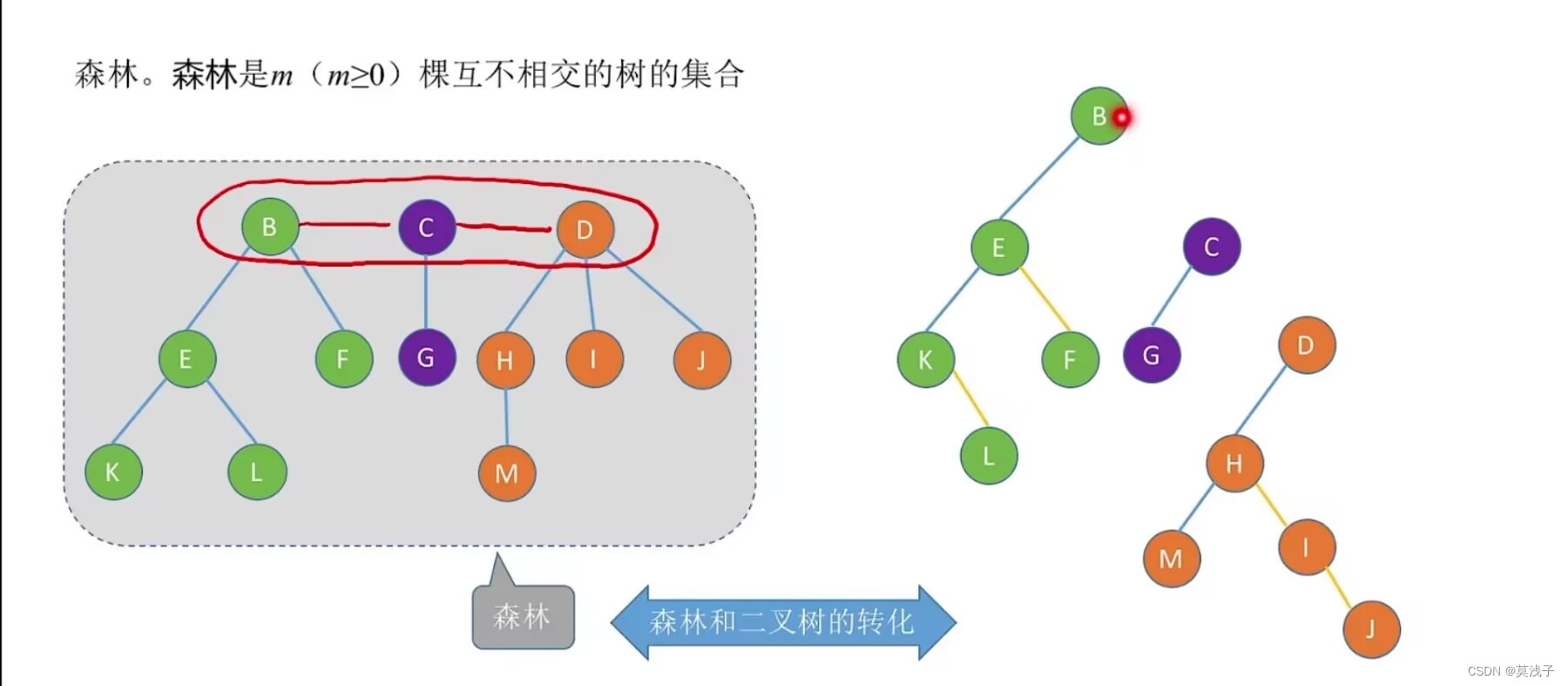
在二叉树中，如果是兄弟关系就在右边，如果是孩子就在左边，本质上，用二叉链表存储森林

树的遍历

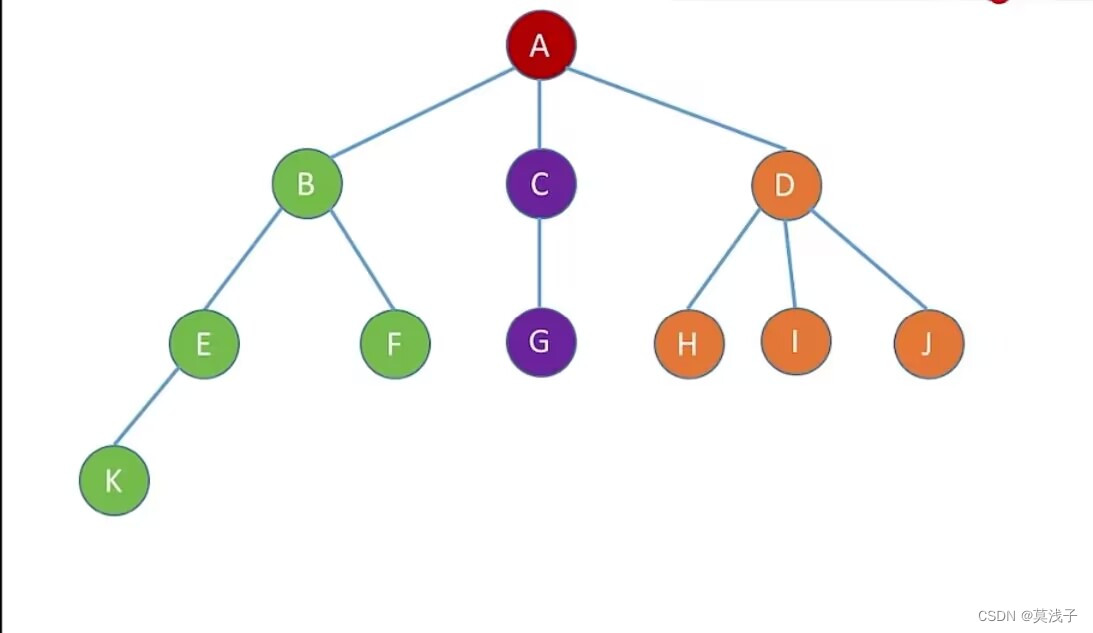
树的先根遍历（深度优先遍历）

先根遍历。若树非空，先访问根结点，在依次对没棵子树进行先根遍历。

上图这样一棵树的先根遍历顺序和二叉树的很像，按照二叉树的方法

//树的先根遍历
void PreOrder(TreeNode *R){
	if(R!=NULL){
		visit(R);     //访问根结点
		while(R还有下一个子树T)
		  PreOrder(T);   //先根遍历下一棵子树
	}
} 

树的后根遍历（树的深度优先遍历）

若树非空，先依次对没棵子树进行后根遍历，最后在访问根结点

上图这样一棵树的后根遍历顺序和二叉树的很像，按照二叉树的方法

代码

//树的后根遍历
void PostOrder(TReeNode *R)
{
	if(R != NULL){
		while(R还有下一个子树T)
		   PodtOrder(T);   //后根遍历下一棵子树
		visit(R)    //访问根结点
	}
} 

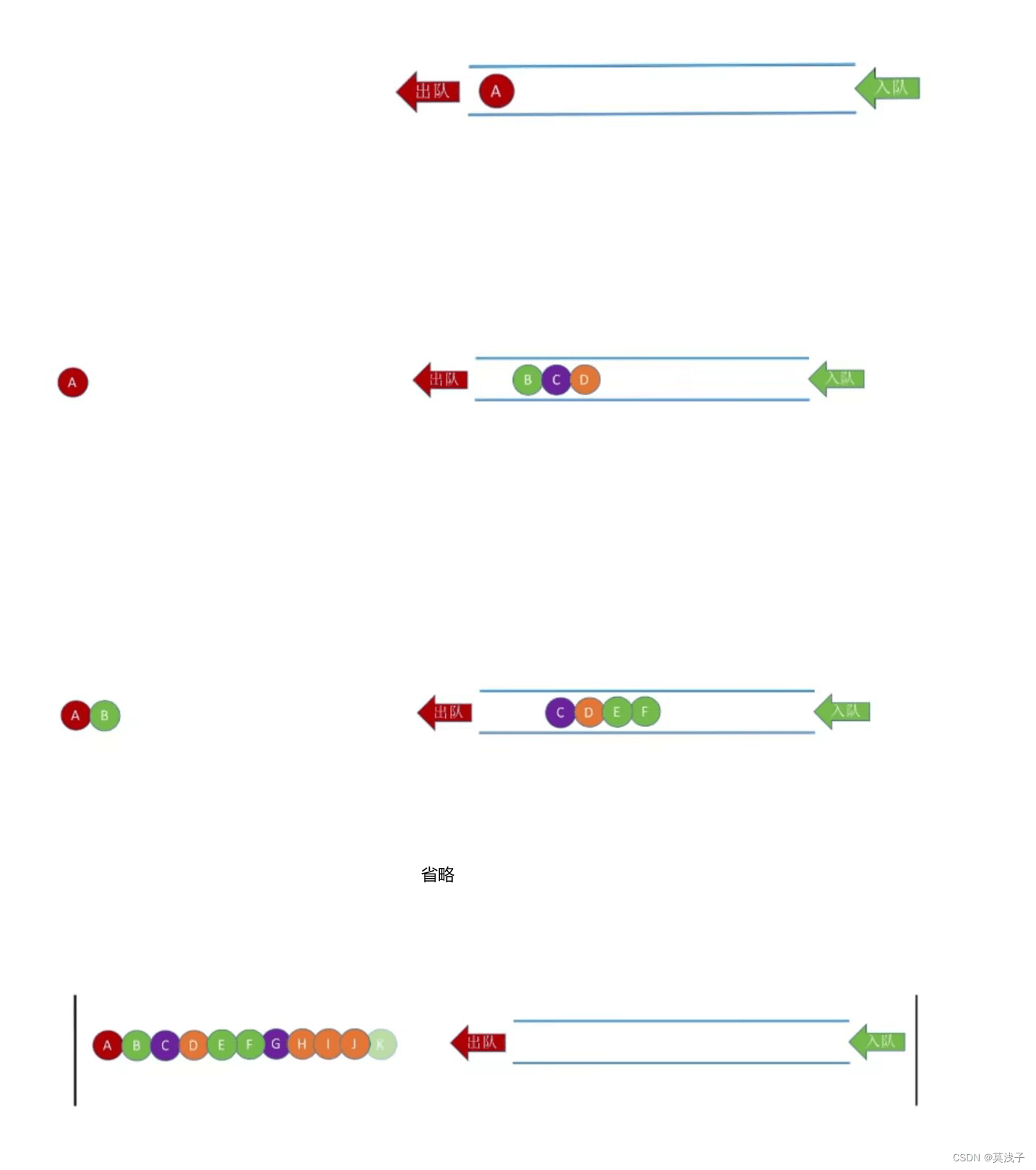
树的层序遍历（广度优先遍历）

层次遍历（用队列实现)

①若树非空，则根节点入队

②若队列非空，队头元素出队并访问，同时将该元素的孩子依次入队

③重复②直到队列为空

如图

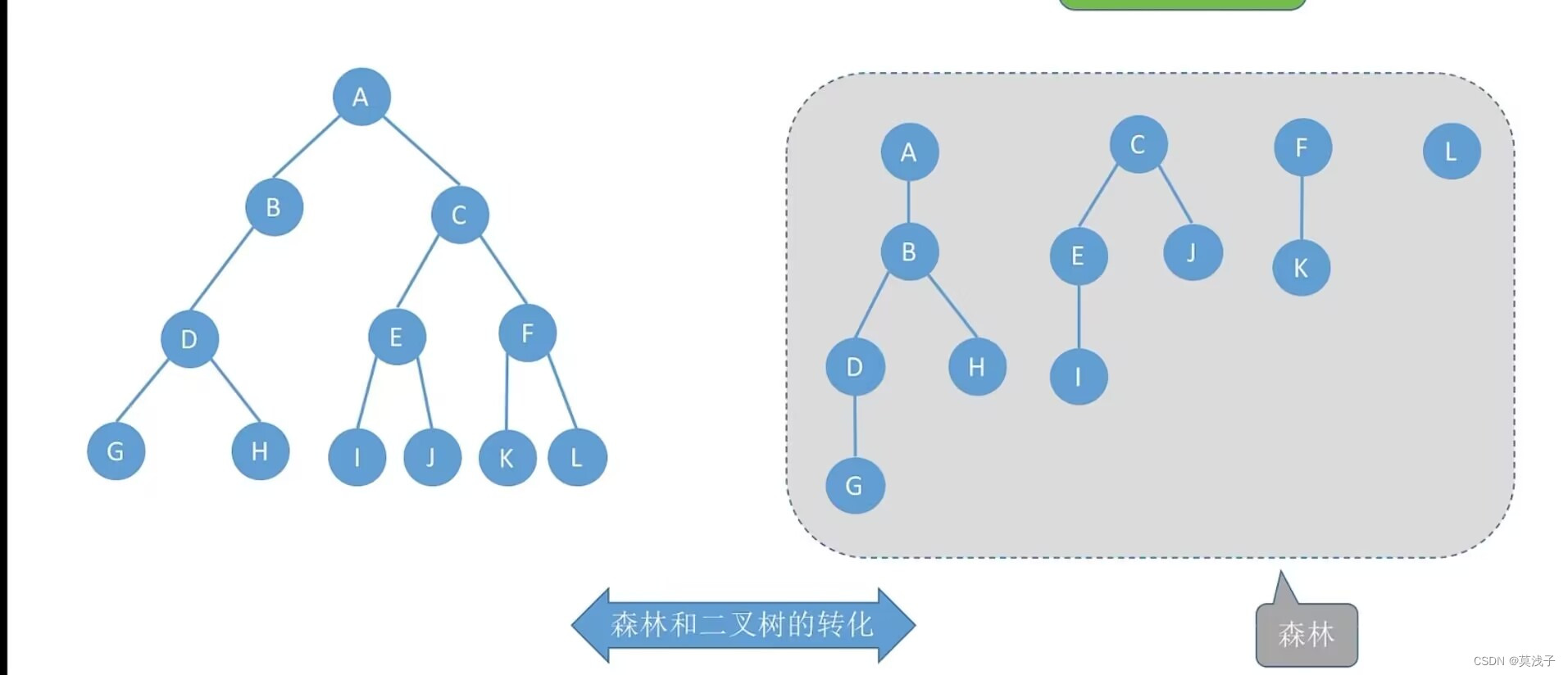
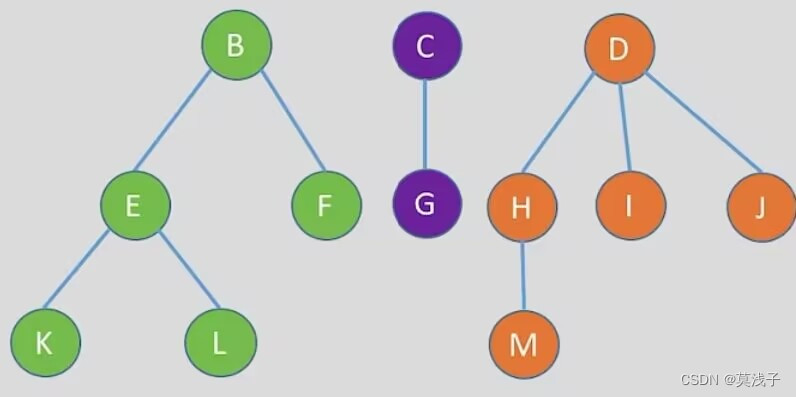
森林的遍历

森林。森林是m (m>0）棵互不相交的树的集合。每棵树去掉根节点后，其各个子树又组成森林。

先序遍历森林

效果等同于依次对各二叉树进行先序遍历

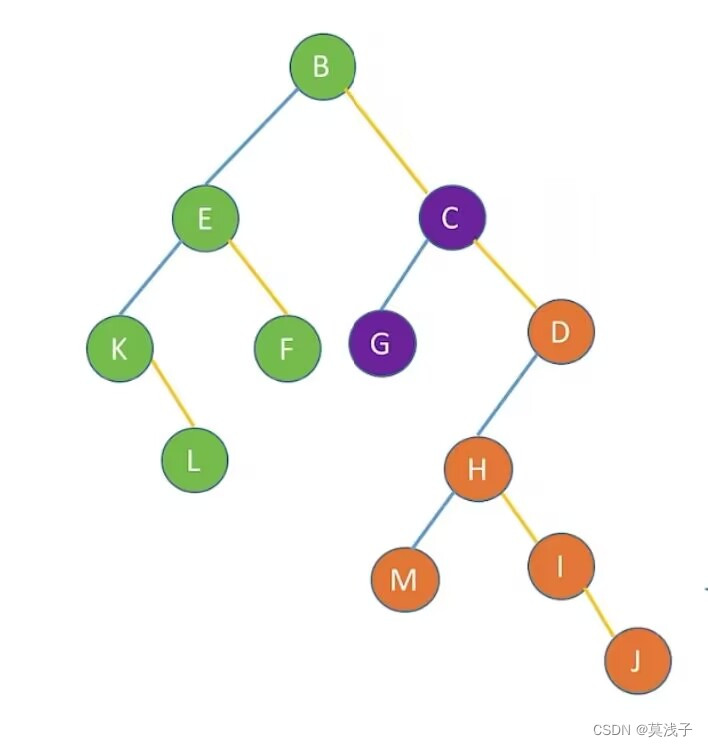
若森林为非空，则按如下规则进行遍历:

1.访问森林中第一棵树的根结点

2.先序遍历第一棵树中根结点的子树森林。

3.先序遍历除去第一棵树之后剩余的树构成的森林。

效果如下

中序遍历森林

效果等同于依次对二叉树进行中序遍历

若森林为非空，则按如下规则进行遍历:

中序遍历森林中第一棵树的根结点的子树森林。

访问第一棵树的根结点。

中序遍历除去第一棵树之后剩余的树构成的森林。

效果如下

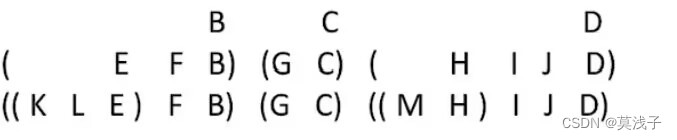
到此这篇关于C语言数据结构中树与森林专项详解的文章就介绍到这了,更多相关C语言树与森林内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！