python机器学习之决策树分类详解

决策树分类与上一篇博客k近邻分类的最大的区别就在于，k近邻是没有训练过程的，而决策树是通过对训练数据进行分析，从而构造决策树，通过决策树来对测试数据进行分类，同样是属于监督学习的范畴。决策树的结果类似如下图：

图中方形方框代表叶节点，带圆边的方框代表决策节点，决策节点与叶节点的不同之处就是决策节点还需要通过判断该节点的状态来进一步分类。

那么如何通过训练数据来得到这样的决策树呢？

这里涉及要信息论中一个很重要的信息度量方式，香农熵。通过香农熵可以计算信息增益。

香农熵的计算公式如下：

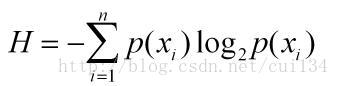
p(xi)代表数据被分在i类的概率，可以通过计算数据集中i类的个数与总的数据个数之比得到，计算香农熵的python代码如下：

from math import log 

def calcShannonEnt(dataSet):
  numEntries=len(dataSet)
  labelCounts={}
  for featVec in dataSet:
    currentLabel=featVec[-1]
    if currentLabel not in labelCounts.keys():
      labelCounts[currentLabel]=0
    labelCounts[currentLabel]+=1
  shannonEnt=0.0
  for key in labelCounts:
    prob=float(labelCounts[key])/numEntries
    shannonEnt-=prob*log(prob,2)
  return shannonEnt

一般来说，数据集中，不同的类别越多，即信息量越大，那么熵值越大，通过计算熵，就可以知道选择哪一个特征能够最好的分开数据，这个特征就是一个决策节点。

下面就可以根据训练数据开始构造决策树。

首先编写一个根据给定特征划分数据集的函数：

#划分数据集，返回第axis轴为value值的数据集
def splitDataSet(dataset,axis,value):
  retDataSet=[]
  for featVec in dataset:
    if featVec[axis]==value:
      reducedFeatVec=featVec[:]
      del(reducedFeatVec[axis])
      retDataSet.append(reducedFeatVec)
  return retDataSet 

下面找出数据集中能够最好划分数据的那个特征，它的原理是计算经过每一个特征轴划分后的数据的信息增益，信息增益越大，代表通过该特征轴划分是最优的。

#选择最好的数据集划分方式，返回最佳的轴
def chooseBestFeatureToSplit(dataset):
  numFeatures=len(dataset[0])-1
  baseEntrypy=calcShannonEnt(dataset)
  bestInfoGain=0.0
  bestFeature=-1
  for i in range(numFeatures):
    featList=[example[i] for example in dataset]
    uniqueVals=set(featList)
    newEntrypy=0.0
    for value in uniqueVals:
      subDataSet=splitDataSet(dataset,i,value)
      prob=len(subDataSet)/float(len(dataset))
      newEntrypy+=prob*calcShannonEnt(subDataSet)
    infoGain=baseEntrypy-newEntrypy        #计算信息增益，信息增益最大，就是最好的划分
    if infoGain>bestInfoGain:
      bestInfoGain=infoGain
      bestFeature=i
  return bestFeature

找出最优的划分轴之后，便可以通过递归来构建决策树，递归有两个终止条件，第一个是程序遍历完所有划分数据集的特征轴，第二 个是每个分支下的所有实例都有相同的分类。那么，这里有一个问题，就是当遍历完所有数据集时，分出来的数据还不是同一类别，这种时候，一般选取类别最多的作为该叶节点的分类。

首先编写一个在类别向量中找出类别最多的那一类：

#计算类型列表中，类型最多的类型
def majorityCnt(classList):
  classCount={}
  for vote in classList:
    if vote not in classCount.keys():
      classCount[vote]=0
    classCount[vote]+=1
  sortedClassCount=sorted(classCount.iteritems(),key=operator.itemgetter(1),reverse=True)
  return sortedClassCount[0][0]

递归创建决策树：

#根据训练数据创建树
def createTree(dataSet,labels):
  myLabels=labels[:]
  classList=[example[-1] for example in dataSet] #类别
  if classList.count(classList[0])==len(classList):#数据集中都是同类
    return classList[0]
  if len(dataSet[0])==1:#训练集中只有一个数据
    return majorityCnt(classList)
  bestFeat=chooseBestFeatureToSplit(dataSet)
  bestFeatLabel=myLabels[bestFeat]
  myTree={bestFeatLabel:{}}
  del(myLabels[bestFeat])
  featValue=[example[bestFeat] for example in dataSet]
  uniqueVal=set(featValue)
  for value in uniqueVal:
    subLabels=myLabels[:]
    myTree[bestFeatLabel][value]=createTree(splitDataSet(dataSet,bestFeat,value),subLabels)
  return myTree

将上述代码保存到tree.py中，在命令窗口输入以下代码：

>>> dataSet=[[1,1,'yes'],
       [1,1,'yes'],
       [1,0,'no'],
       [0,1,'no'],
       [0,1,'no']]
>>> labels=['no sufacing','flippers']
>>> tree.createTree(dataSet,labels)
{'no sufacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}

就得到了决策树的结构，可以画出树的结构图

上面数据的实际意义是通过生物特征，来判断是否属于鱼类，第一列数据中1代表在水中可以生存，0代表在水中不可以生存。第二列中1代表有脚蹼，0代表没有脚蹼。yes是鱼类，no不是鱼类。label是训练数据中每一列代表的意义。那么通过训练数据我们就构造出了决策树，由图可知，我们首先可以根据第一列特征，即在水中是否可以生存来进行第一步判断，不可以生存的肯定不是鱼类，可以生存的还要看是否有脚蹼，有脚蹼的才是鱼类。

不难看出，决策树最大的优势就是它的数据形式易于理解，分类方式直观。

训练出决策树之后，我们就可以根据根据决策树来对新的测试数据进行分类。

分类代码如下：

#根据决策树分类
def classify(inputTree,featLabels,testVec):
  firstStr=inputTree.keys()[0]
  secondDict=inputTree[firstStr]
  featIndex=featLabels.index(firstStr)
  for key in secondDict.keys():
    if testVec[featIndex]==key:
      if type(secondDict[key]).__name__=='dict':
        classLabel=classify(secondDict[key],featLabels,testVec)
      else:
        classLabel=secondDict[key]
  return classLabel

这里有一个通过决策数算法进行分类的一个实例，眼科医生是如何判断患者需要佩戴隐形眼镜的类型的。

判断的结果有三种，硬材料，软材料和不适合佩戴。

训练数据采用隐形眼镜数据集，数据集来自UCI数据库，它包含了很多患者眼部状况的观察条件以及医生推荐的眼镜类型。

数据集如下：

测试代码如下：

def example():
  fr=open('lenses.txt')
  lenses=[inst.strip().split('\t') for inst in fr.readlines()]
  lensesLabels=['age','prescript','astigmatic','tearRate']
  lensesTree=createTree(lenses,lensesLabels)
  return lensesTree 

结果：

决策树结构如下：

这样，医生便可以一步步的观察来最终得知该患者适合什么材料的隐形眼镜了。

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。