PHP实现八皇后算法

回溯算法实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。回溯法是一种选优搜索法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。

回溯算法的基本思想是：从一条路往前走，能进则进，不能进则退回来，换一条路再试。

八皇后问题，是一个古老而著名的问题，是回溯算法的典型案例。该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出：在8×8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。

这边先以4皇后来解释解决步骤：

详细说明

在第一行有四种可能，选择第一个位置放上皇后

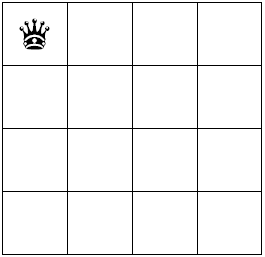
第二行原本可以有四种可能摆放，但是第一第二个已经和第一行的皇后冲突了，因此只剩下第三第四个格子了，先选择第三个格子

接下来是第三行，根据规则可以看出，第三行已经没有位置放了，因为都跟第一第二行的皇后冲突，此时返回到第二行第四个

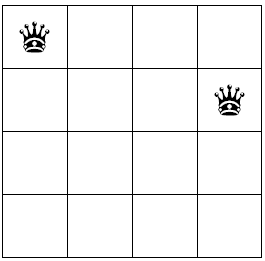
继续来到第三行，发现只有第二个满足条件

然后发现第四行已经不能放了，只能继续返回，返回到第一行，开始下一种可能

按照 1-5 的步骤，可以找到下面的其中一种解法

总而言之，回溯法就是开始一路到底，碰到南墙了就返回走另外一条路，有点像穷举法那样走遍所有的路。

PHP代码实现：

<?php

class Backtracking {

 protected $chessboard;  // 棋盘 二维数组 表示坐标轴
 protected $N;      // N表示几皇后
 protected $has_set_x;  // 已经设置的x坐标数组 已经设置的x坐标就不能重复了，用于检查坐标是否可用
 protected $has_set_y;  // 已经设置的y坐标数组 已经设置的y坐标就不能重复了，用于检查坐标是否可用
 protected $has_set_site; // 已经设置的点

 function __construct($N) {
 // 初始化数据
 $this->N = $N;
 $this->chessboard = array();
 for ($i=0; $i < $N; $i++) {
  for ($j=0; $j < $N; $j++) {
  $this->chessboard[$i][$j] = 0;
  }
 }
 $this->has_set_x = array();
 $this->has_set_y = array();
 $this->has_set_site = array();
 }

 // 获取排列
 public function getPermutation($is_get_on = true) { // is_get_on 是否获取一种排列 true:是 false:获取所有排列
 $current_n = 0; // 当前设置第几个皇后
 $start_x = 0;  // 当前的x坐标 从x开始放置尝试
 $permutation_array = array(); // 全部皇后放置成功的排列数组
 while ($current_n < $this->N && $current_n >= 0) {
  $site_result = $this->setQueenSite($current_n, $start_x); // 设置皇后位置
  if($site_result == true && $current_n + 1 >= $this->N) { // 如果最后的皇后位置放置成功则记录信息
  $permutation_array[] = array_merge($this->has_set_site, array(array('x' => $site_result['x'], 'y' => $site_result['y'])));
  if($is_get_on == false) { // 如果是获取所有排列，则设置当前放置失败，让程序回溯继续找到其他排列
   $site_result = false;
  }
  }
  if($site_result == true) {
  $this->chessboard[$site_result['x']][$site_result['y']] = 1;
  $this->has_set_x[] = $site_result['x'];
  $this->has_set_y[] = $site_result['y'];
  $this->has_set_site[] = array('x' => $site_result['x'], 'y' => $site_result['y']);
  $current_n++; // 皇后位置放置成功，继续设置下一个皇后，重置下一个皇后的x坐标从0开始
  $start_x = 0;
  }else {
  // 当前皇后找不到放置的位置，则需要回溯到上一步
  $previous_site = array_pop($this->has_set_site); // 找到上一步皇后的位置
  if(!empty($previous_site)) {
   $start_x = $previous_site['x'] + 1; // 让上一步的皇后的x坐标+1继续尝试放置
   $this->deleteArrayValue($this->has_set_x, $previous_site['x']);
   $this->deleteArrayValue($this->has_set_y, $previous_site['y']);
   $this->chessboard[$previous_site['x']][$previous_site['y']] = 0;
  }
  $current_n--; // 回溯到上一步，即让一个皇后x坐标+1继续尝试放置
  }
 }
 return $permutation_array;
 }

 // 设置皇后位置
 public function setQueenSite($n, $start_x) {
 $start_y = $n;
 if($start_x >= $this->N) return false;
 $check_result = $this->checkQueenSite($start_x, $start_y); // 检查当前是否可放置
 if($check_result == true) {
  return array('x' => $start_x, 'y' => $start_y);
 }else { // 不可放置，则x坐标+1，继续尝试
  $start_x++;
  return $this->setQueenSite($n, $start_x);
 }
 }

 // 检查皇后位置是否正确
 public function checkQueenSite($x, $y) {
 // 判断当前坐标的横、纵、斜线是否存在已经放置的皇后
 if(in_array($x, $this->has_set_x)) return false;
 if(in_array($y, $this->has_set_y)) return false;
 $operate_array = array(
  array('operate_x' => '+', 'operate_y' => '+'),
  array('operate_x' => '-', 'operate_y' => '-'),
  array('operate_x' => '+', 'operate_y' => '-'),
  array('operate_x' => '-', 'operate_y' => '+')
 );
 foreach ($operate_array as $key => $value) {
  $diagonal_x = $x;
  $diagonal_y = $y;
  while (true) {
  eval("\$diagonal_x=$diagonal_x {$value['operate_x']} 1;");
  eval("\$diagonal_y=$diagonal_y {$value['operate_y']} 1;");
  if($diagonal_x >= $this->N || $diagonal_y >= $this->N || $diagonal_x < 0 || $diagonal_y < 0) break;
  if($this->chessboard[$diagonal_x][$diagonal_y] == 1) return false;
  }
 }
 return true;
 }

 // 删除数组元素
 public function deleteArrayValue(&$array, $value) {
 $delete_key = array_search($value, $array);
 array_splice($array, $delete_key, 1);
 }

}

$N = 8; // 8表示获取8皇后的排列组合
$backtracking = new Backtracking($N);
$permutations = $backtracking->getPermutation(false);
var_dump($permutations); // 输出92种排列

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。