JavaScript中关于递归与回溯的实例详解

目录

• 何为递归
• 构成递归条件
• 关于回溯
• 实际业务
• 组合问题

何为递归

递归作为一种算法在程序设计语言中广泛应用。 一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解，递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算，大大地减少了程序的代码量。递归的能力在于用有限的语句来定义对象的无限集合。需要注意的是，递归必须要用边界条件，否则很容易导致死循环

构成递归条件

• 子问题须与原始问题为同样的事，且更为简单
• 不能无限制地调用本身，须有个出口，化简为非递归状况处理

但是递归函数并不容易一下子就能想的出来，所以我们可以先通过一个子问题来逐步延申。

问题一： 假设我们需要求1+2+3+...+100的值，我们很容易想出下面的代码

 function calcNum(n) {
      let sum = 0
      for (let i = 0; i <= 100; i++) {
        sum += i
      }
      return sum
    }
    console.log(calcNum()) // 5050

这样的代码是不满足于递归中，直接或者间接调用本身的定义。那么如何变成递归版本呢？(任何的循环，都可以写成递归)

• 寻找相同的子问题 该题目相同的子问题很明显是sum+=i，该过程是重复调用的过程。
• 寻找终止条件 寻找递归的终止条件，该问题的终止条件是i>100的情况

这两大要素都找到了，就很容易写出下面的递归版本

function calcNum(n) {
      let sum = 0
      function dfs(n) {
        if (n > 100) {
          return
        }
        sum += n
        n++
        dfs(n)
      }
      dfs(n)
      return sum
    }
    console.log(calcNum(1)) // 5050

关于回溯

递归一定伴随着回溯，那么什么是回溯呢？以上面的代码为例子，我们分别在这两处地方输出n的值

function calcNum(n) {
      let sum = 0
      function dfs(n) {
        if (n > 100) {
          return
        }
        sum += n
        n++
        console.log(n, '递归前的n')
        dfs(n)
        console.log(n, '递归后的n')
      }
      dfs(n)
      return sum
    }

毫无疑问，"递归前的n"会按照1-100输出，而"递归后的n"则会100-1输出，这就说明了一个很重要的知识点，递归函数是类似一个栈迭代的过程，它的值输出的顺序为先进后出。通俗一点说，递归函数后面的参数，会反转输出。

要想理解回溯的含义，最为经典的还是二叉树的遍历。二叉树的遍历，又分为前序遍历，中序遍历，后序遍历，分别通过代码来感受一下这三种遍历的方式。 前序遍历

// 基本结构
 const treeNode = {
      val: 1,
      left: null,
      right: {
        val: 2,
        left: {
          val: 3,
          left: null,
          right: null
        },
        right: null
      }
    }

来看下leetcode 前序遍历原题

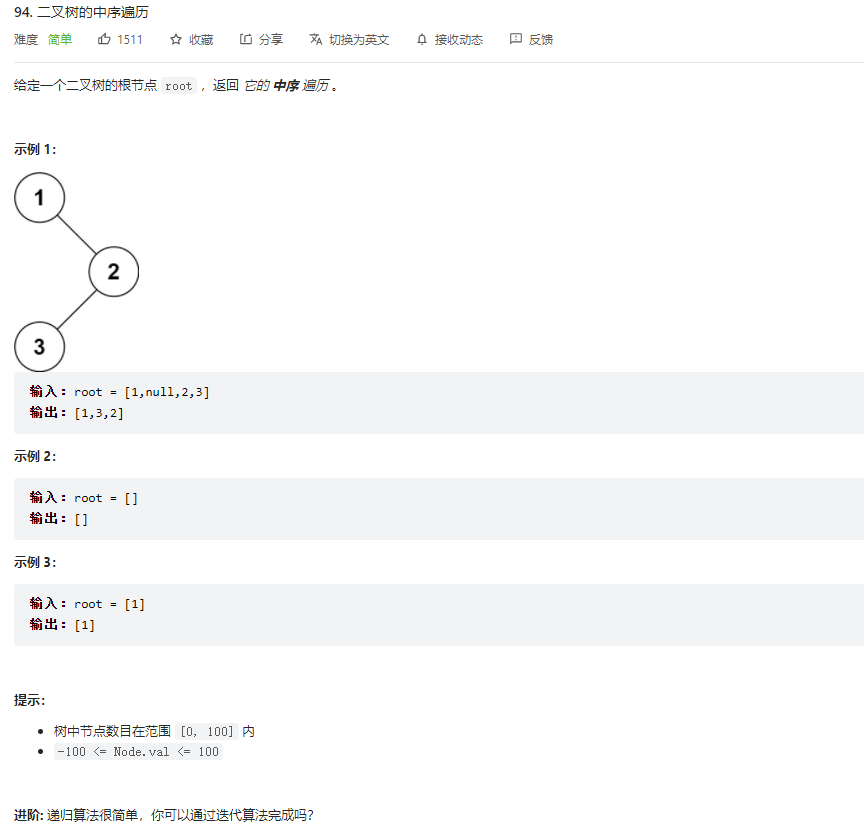
const root = {
      val: 5,
      left: {
        val: 4,
        left: {
          val: 1,
          right: null,
          left: null
        },
        right: {
          val: 2,
          right: null,
          left: null
        }
      },
      right: {
        val: 6,
        left: {
          val: 7,
          left: null,
          right: null
        },
        right: {
          val: 8,
          left: null,
          right: null
        }
      }
    }
    function getRoot(root) {
      const res = []
      function dfs(root) {
        if (!root) {
          return
        }
        res.push(root.val)
        dfs(root.left)
        dfs(root.right)
      }
      dfs(root)
      return res
    }
    console.log(getRoot(root)) // 5 4 1 2 6 7 8

中序遍历

function getRoot(root) {
      const res = []
      function dfs(root) {
        if (!root) {
          return
        }
        dfs(root.left)
        res.push(root.val)
        dfs(root.right)
      }
      dfs(root)
      return res
    }
    console.log(getRoot(root)) // 1 4 2 5 6 7 8

后续遍历

function getRoot(root) {
      const res = []
      function dfs(root) {
        if (!root) {
          return
        }
        dfs(root.left)
        dfs(root.right)
        res.push(root.val)
      }
      dfs(root)
      return res
    }
    console.log(getRoot(root)) // 1 2 4 7 8 6 5

在写递归的时候，时刻都要注意边界，以上场景的边界，则是找不到节点（节点为null）的时候，就退出。

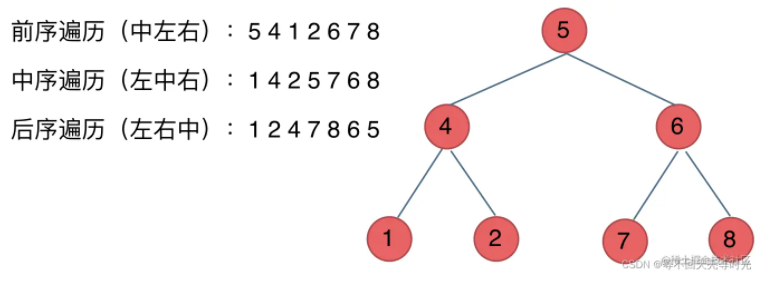
通过输出的结果可以得知以下规律：

• 前序遍历：中左右
• 中序遍历：左中右
• 后序遍历：左右中

而实现该规律的主要依据，是通过递归的回溯导致，我们以中序遍历为例子：

 dfs(root.left)
 res.push(root.val)
 dfs(root.right)

当第一个dfs(root.left)递归结束后，就会弹出'1'的节点，然后就进了dfs(root.right)的节点，发现是个null，说明这个dfs(root.right)递归结束，那么此时则回到了'4'的节点，然后就进入了dfs(root.right)节点...

实际业务

二叉树的遍历，其实类比于我们常见操作菜单树，或着树形结构的操作...

let tree = [
  {
    id: '1',
    title: '节点1',
    children: [
      {
        id: '1-1',
        title: '节点1-1'
      },
      {
        id: '1-2',
        title: '节点1-2'
      }
    ]
  },
  {
    id: '2',
    title: '节点2',
    children: [
      {
        id: '2-1',
        title: '节点2-1'
      }
    ]
  }
]

当我们要寻找遍历每个节点的时候，同样需要注意边界，当我们操作的数据没有的时候或者不存在的时候，则退出当次遍历。

 function getRootData(tree) {
      const res = []
      function dfs(tree) {
        if (!tree || tree.length === 0) {
          return res
        }
        for (let i = 0; i < tree.length; i++) {
          const t = tree[i]
          if (t.children && t.children.length > 0) {
            dfs(t.children) // 开始递归
          } else {
            res.push(t.title) //  ['节点1-1', '节点1-2', '节点2-1']
          }
        }
      }
      dfs(tree)
      return res
    }

可能有人会有疑问，这也没有利用到回溯的操作啊，那么我就换个场景，假如我给个你节点的id，你帮我找出他所有的父节点，那么你可能会怎么操作呢？

 const tree = [
      {
        id: '1',
        title: '节点1',
        children: [
          {
            id: '1-1',
            title: '节点1-1'
          },
          {
            id: '1-2',
            title: '节点1-2'
          }
        ]
      },
      {
        id: '2',
        title: '节点2',
        children: [
          {
            id: '2-1',
            title: '节点2-1',
            children: [
              {
                id: '2-1-1',
                title: '节点2-1-1'
              }
            ]
          }
        ]
      }
    ]
    function pathTree(tree, id) {
      const res = []
      function dfs(tree, path) {
        if (!tree || tree.length === 0) {
          return
        }
        for (let i = 0; i < tree.length; i++) {
          const t = tree[i]
          path.push(t.id)
          if (path.includes(id)) {
            res.push(path.slice())
          }
          if (t.children && t.children.length > 0) {
            dfs(t.children, path)
          }
          path.pop() // 路径回溯
        }
      }
      dfs(tree, [])
      return res
    }
    console.log(pathTree(tree, '2-1-1')) // [2,2-1,2-1-1]

其实以上核心的代码为path.pop()，为什么需要这句代码呢？我们可以通过leetcode上的排列组合问题来进行讨论。

组合问题

经典的组合问题

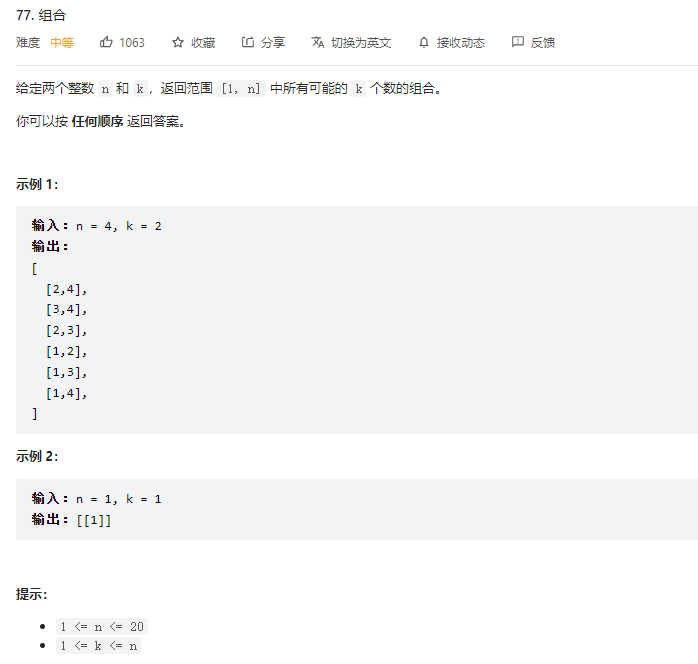
以上面题目为例子，从1-4(n)的数字中，排列2(k)个数的组合。解这个题目，可以使用暴力的做法，嵌套for循环来完成该功能。

function combine(n) {
      const res = []
      for (let i = 1; i <= n; i++) {
        for (let j = i + 1; j <= n; j++) {
          res.push([i, j])
        }
      }
      return res
    }

  console.log(combine(4), 'res') // [1,2][1,3][1,4][2,3][3,4][2,4]

细心朋友就会发现，它嵌套for次数则是等于它排列(k)的次数，那么我假如k的次数是10，或者20，那么岂不是要嵌套10个或者20个for循环。这套代码写下来，估计是个人都会晕了。在以上代码块中也可以发现重复的子问题也就是for循环，它想要的结果则为当我们找个了k个数的时候就停止。那么我们可以尝试通过递归来解决该问题（递归for循环），但是这样的过程还是很抽象的，需要借助图例理解。（任何的组合问题，都可以理解成为n叉树的遍历）

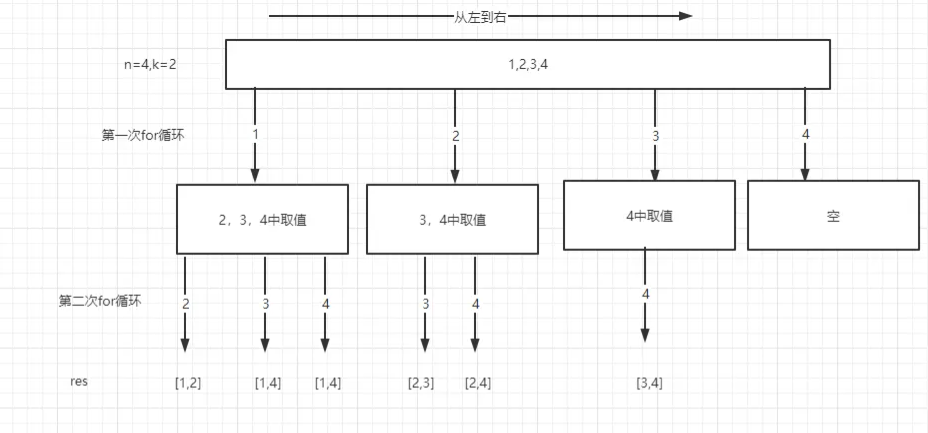
 function combine(n, k) {
      const res = []
      function dfs(n, path, startIndex) {
        if (path.length === k) {
          res.push(path.slice())
          return
        }
        for (let i = startIndex; i <= n; i++) {
          path.push(i)
          dfs(n, path, i + 1)
          path.pop()
        }
      }
      dfs(n, [], 1)
      return res
    }

当我们选择到了[1,2]之后，则需要回到1的位置，因为这个时候需要选择3选项，形成[1,3]，那么回到'1'的操作，就类似于二叉树遍历回到父节点的操作，如果此时我们不操作，path.pop()，那么此时就会形成了[1,2,3]，这样的结果明显不是我们想要，所以在操作push "3"的过程，需要先把2给pop掉。而递归的终止条件则为当路径的长度等于k的时候则退出。 另外在函数体中，还发现了startIndex的存在，这个是作为横向for循环开始的位置，我们结合上面两个for循环的代码，是不是发现了j = i + 1的操作，而这个startIndex则是还原了这个操作而已。

到此这篇关于JavaScript中关于递归与回溯的实例详解的文章就介绍到这了,更多相关JavaScript递归 回溯内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！