Python查找算法之分块查找算法的实现

一、分块查找算法

分块查找是二分法查找和顺序查找的改进方法，分块查找要求索引表是有序的，对块内结点没有排序要求，块内结点可以是有序的也可以是无序的。

分块查找就是把一个大的线性表分解成若干块，每块中的节点可以任意存放，但块与块之间必须排序。与此同时，还要建立一个索引表，把每块中的最大值作为索引表的索引值，此索引表需要按块的顺序存放到一个辅助数组中。查找时，首先在索引表中进行查找，确定要找的结点所在的块。由于索引表是排序的，因此，对索引表的查找可以采用顺序查找或二分查找；然后，在相应的块中采用顺序查找，即可找到对应的结点。

例如，有这样一列数据：23、43、56、78、97、100、120、135、147、150。如下图所示：

想要查找的数据是 150，使用分块查找法步骤如下：

步骤1：将上图所示的数据进行分块，按照每块长度为 4 进行分块，分块情况如下图所示：

说明：每块的长度是任意指定的，博主在这里用的长度为4，读者可以根据自己的需要指定每块长度。

步骤2：选取各块中的最大关键字构成一个索引表，即选取上图所示的各块的最大值，第一块最大的值是 78，第二块最大的值是 135，第三块最大值是 155，形成的索引表如下图所示：

步骤3：用顺序查找或者二分查找判断想要查找数据 150 在上图所示的索引表中的哪块内容中，这里博主用的是二分查找法，即先取中间值 135 与 150 比较，如下图所示：

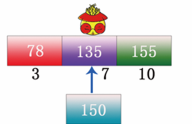
步骤4：结果是中间位置的数据 135 比目标数据 150 小，因此目标数据在 135 的下一块内。将数据定位在第 3 块内，此时将第 3 块内的数据取出，进行顺序比较，如下图所示：

步骤5：通过顺序查找第 3 块的内容，终于在第 9 个位置找到目标数，此时分块查找结束。

总结：至此，分块查找算法已经讲解完毕。通过和二分查找法和顺序查找法对比来看，分块查找的速度虽然不如二分查找算法，但比顺序查找算法快得多。当数据很多且块数很大时，对索引表可以采用二分查找，这样能够进一步提高查找的速度。

二、实例：实现分块查找算法

具体代码如下：

def search(data, key):  # 用二分查找 想要查找的数据在哪块内
    length = len(data)  # 数据列表长度
    first = 0  # 第一位数位置
    last = length - 1  # 最后一个数据位置
    print(f"长度:{length} 分块的数据是:{data}")  # 输出分块情况
    while first <= last:
        mid = (last + first) // 2  # 取中间位置
        if data[mid] > key:  # 中间数据大于想要查的数据
            last = mid - 1  # 将last的位置移到中间位置的前一位
        elif data[mid] < key:  # 中间数据小于想要查的数据
            first = mid + 1  # 将first的位置移到中间位置的后一位
        else:
            return mid  # 返回中间位置
    return False

# 分块查找
def block(data, count, key):  # 分块查找数据，data是列表，count是每块的长度，key是想要查找的数据
    length = len(data)  # 表示数据列表的长度
    block_length = length // count  # 一共分的几块
    if count * block_length != length:  # 每块长度乘以分块总数不等于数据总长度
        block_length += 1  # 块数加1
    print("一共分", block_length, "块")  # 块的多少
    print("分块情况如下：")
    for block_i in range(block_length):  # 遍历每块数据
        block_data = []  # 每块数据初始化
        for i in range(count):  # 遍历每块数据的位置
            if block_i * count + i >= length:  # 每块长度要与数据长度比较，一旦大于数据长度
                break  # 就退出循环
            block_data.append(data[block_i * count + i])  # 每块长度要累加上一块的长度
        result = search(block_data, key)  # 调用二分查找的值
        if result != False:  # 查找的结果不为False
            return block_i * count + result  # 就返回块中的索引位置
    return False

data = [23, 43, 56, 78, 97, 100, 120, 135, 147, 150, 155]  # 数据列表
result = block(data, 4, 150)  # 第二个参数是块的长度，最后一个参数是要查找的元素
print("查找的值得索引位置是:", result)  # 输出结果

运行结果如下图所示：

从上面的运行结果看到，当查找 150 时，查找结果完全符合上述描述的步骤。

到此这篇关于Python查找算法之分块查找算法的实现的文章就介绍到这了,更多相关Python 分块查找算法内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！

赞 (0)

相关推荐

  • python二分查找算法的递归实现方法

    本文实例讲述了python二分查找算法的递归实现方法.分享给大家供大家参考,具体如下: 这里先提供一段二分查找的代码: def binarySearch(alist, item): first = 0 last = len(alist)-1 found = False while first<=last and not found: midpoint = (first + last)//2 if alist[midpoint] == item: found = True else: if ite

  • Python实现二分查找算法实例

    本文实例讲述了Python实现二分查找算法的方法.分享给大家供大家参考.具体实现方法如下: #!/usr/bin/env python import sys def search2(a,m): low = 0 high = len(a) - 1 while(low <= high): mid = (low + high)/2 midval = a[mid] if midval < m: low = mid + 1 elif midval > m: high = mid - 1 else:

  • Python实现查找数组中任意第k大的数字算法示例

    本文实例讲述了Python实现查找数组中任意第k大的数字算法.分享给大家供大家参考,具体如下: 模仿partion方法,当high=low小于k的时候,在后半部分搜索,当high=low大于k的时候,在前半部分搜索.与快排不同的是,每次都减少了一半的排序. def partitionOfK(numbers, start, end, k): if k < 0 or numbers == [] or start < 0 or end >= len(numbers) or k > end

  • python快速查找算法应用实例

    本文实例讲述了Python快速查找算法的应用,分享给大家供大家参考. 具体实现方法如下: import random def partition(list_object,start,end): random_choice = start #random.choice(range(start,end+1)) #把这里的start改成random()效率会更高些 x = list_object[random_choice] i = start j = end while True: while li

  • python有序查找算法 二分法实例解析

    python有序查找算法 二分法实例解析

    这篇文章主要介绍了python有序查找算法 二分法实例解析,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友可以参考下 二分法是一种快速查找的方法,时间复杂度低,逻辑简单易懂,总的来说就是不断的除以2除以2... 但是需要注意: 待查找的序列区间单调有序 例如需要查找有序数组arr里面的某个关键字key的位置,那么首先确认arr的中位数或者中点center,下面分为三种情况: 假如arr[center]>key,说明key在arr中心左边范围: 假如arr[

  • Python中的二叉树查找算法模块使用指南

    python中的二叉树模块内容: BinaryTree:非平衡二叉树  AVLTree:平衡的AVL树  RBTree:平衡的红黑树 以上是用python写的,相面的模块是用c写的,并且可以做为Cython的包. FastBinaryTree  FastAVLTree  FastRBTree 特别需要说明的是:树往往要比python内置的dict类慢一些,但是它中的所有数据都是按照某个关键词进行排序的,故在某些情况下是必须使用的. 安装和使用 安装方法 安装环境: ubuntu12.04, py

  • Python有序查找算法之二分法实例分析

    本文实例讲述了Python有序查找算法之二分法.分享给大家供大家参考,具体如下: 二分法是一种快速查找的方法,时间复杂度低,逻辑简单易懂,总的来说就是不断的除以2除以2... 例如需要查找有序数组arr里面的某个关键字key的位置,那么首先确认arr的中位数或者中点center,下面分为三种情况: ① 假如arr[center]>key,说明key在arr中心左边范围: ② 假如arr[center]<key,说明key在arr中心右边范围: ③ 假如arr[center]=key,说明key

  • Python实现在某个数组中查找一个值的算法示例

    第一种算法思路: 第一步:随机出来一个数组的下标 第二步:判断下标对应的值是否等于被查找的值,是的话终止,已找到,否的话转第三步. 第三步:判断是否随机完数组的所有下标,是的话终止,没找到,否的话转第一步. 代码如下: #本程序的功能是在字典中查找存在某个值 import random di = {'a':1,'b':2,'c':3,'d':4,'e':5,'f':6} key = 2 di1 = {} while True: tmp = random.choice(di.keys()) #随机

  • python实现二分查找算法

    二分查找算法:简单的说,就是将一个数组先排序好,比如按照从小到大的顺序排列好,当给定一个数据,比如target,查找target在数组中的位置时,可以先找到数组中间的数array[middle]和target进行比较,当它比target小时,那么target一定是在数组的右边,反之,则target在数组的左边,比如它比target小,则下次就可以只比较[middle+1, end]的数,继续使用二分法,将它一分为二,直到找到target这个数返回或者数组全部遍历完成(target不在数组中) 优

  • Python查找算法之分块查找算法的实现

    Python查找算法之分块查找算法的实现

    一.分块查找算法 分块查找是二分法查找和顺序查找的改进方法,分块查找要求索引表是有序的,对块内结点没有排序要求,块内结点可以是有序的也可以是无序的. 分块查找就是把一个大的线性表分解成若干块,每块中的节点可以任意存放,但块与块之间必须排序.与此同时,还要建立一个索引表,把每块中的最大值作为索引表的索引值,此索引表需要按块的顺序存放到一个辅助数组中.查找时,首先在索引表中进行查找,确定要找的结点所在的块.由于索引表是排序的,因此,对索引表的查找可以采用顺序查找或二分查找:然后,在相应的块中采用顺序

  • Python查找算法之折半查找算法的实现

    Python查找算法之折半查找算法的实现

    一.折半查找算法 折半查找算法又称为二分查找算法,折半查找算法是将数据分割成两等份,首先用键值(要查找的数据)与中间值进行比较.如果键值小于中间值,可确定要查找的键值在前半段:如果键值大于中间值,可确定要查找的键值在后半段.然后对前半段(后半段)进行分割,将其分成两等份,再对比键值.如此循环比较.分割,直到找到数据或者确定数据不存在为止.折半查找的缺点是只适用于已经初步排序好的数列:优点是查找速度快. 生活中也有类似于折半查找的例子,例如,猜数字游戏.在游戏开始之前,首先会给出一定的数字范围(例

  • Python机器学习实战之k-近邻算法的实现

    Python机器学习实战之k-近邻算法的实现

    目录 K-近邻算法概述 工作原理 实施KNN算法 示例:手写识别系统 K-近邻算法概述 简单地说, k-近邻算法采用测量不同特征值之间的距离方法进行分类. k-近邻算法 优点:精度高.对异常值不敏感.无数据输入假定. 缺点: 计算复杂度高.空间复杂度高. 适用数据范围: 数值型和标称型. 工作原理 存在一个样本数据集合, 也称作训练样本集, 并且样本集中每个数据都存在标签, 知道样本集中每一数据与所属分类的对应关系. 输入没有标签的新数据后, 将新数据的每个特征与样本集中数据对应的特征进行比较,

  • 查找算法之二分查找的C++实现

    二分查找 二分查找算法,说白了就是在有序的数组里面给予一个存在数组里面的值key,然后将其先和数组中间的比较,如果key大于中间值,进行下一次mid后面的比较,直到找到相等的,就可以得到它的位置. 前提:线性表中的记录必须是关键字有序(通常从小到大),线性表必须采用顺序存储. 基本思想:取中间记录作为比较对象,若给定值与中间记录的关键字相等,则查找成功:若给定值小于中间记录的关键字,则在中间记录的左半区继续查找:否则,在右半区查找.不断重复,直到查找成功或查找失败为止. #include<ios

  • python机器学习案例教程——K最近邻算法的实现

    K最近邻属于一种分类算法,他的解释最容易,近朱者赤,近墨者黑,我们想看一个人是什么样的,看他的朋友是什么样的就可以了.当然其他还牵着到,看哪方面和朋友比较接近(对象特征),怎样才算是跟朋友亲近,一起吃饭还是一起逛街算是亲近(距离函数),根据朋友的优秀不优秀如何评判目标任务优秀不优秀(分类算法),是否不同优秀程度的朋友和不同的接近程度要考虑一下(距离权重),看几个朋友合适(k值),能否以分数的形式表示优秀度(概率分布). K最近邻概念: 它的工作原理是:存在一个样本数据集合,也称作为训练样本集,并

  • 详解Python查找算法的实现(线性、二分、分块、插值)

    详解Python查找算法的实现(线性、二分、分块、插值)

    目录 1. 线性查找 2. 二分查找 3. 插值查找 4. 分块查找 5. 总结 查找算法是用来检索序列数据(群体)中是否存在给定的数据(关键字),常用查找算法有: 线性查找:线性查找也称为顺序查找,用于在无序数列中查找. 二分查找:二分查找也称为折半查找,其算法用于有序数列. 插值查找:插值查找是对二分查找算法的改进. 分块查找:又称为索引顺序查找,它是线性查找的改进版本. 树表查找:树表查找又可分二叉查找树.平衡二叉树查找. 哈希查找:哈希查找可以直接通过关键字查找到所需要数据. 因树表查找

  • Python实现七大查找算法的示例代码

    Python实现七大查找算法的示例代码

    查找算法 -- 简介 查找(Searching)就是根据给定的某个值,在查找表中确定一个其关键字等于给定值的数据元素.     查找表(Search Table):由同一类型的数据元素构成的集合     关键字(Key):数据元素中某个数据项的值,又称为键值     主键(Primary Key):可唯一的标识某个数据元素或记录的关键字 查找表按照操作方式可分为:         1.静态查找表(Static Search Table):只做查找操作的查找表.它的主要操作是:         ①

  • Python 语言实现六大查找算法

    Python 语言实现六大查找算法

    目录 一.顺序查找算法 二.折半查找算法 三.插补查找算法 四.哈希查找算法 五.分块查找算法 六.斐波那契查找算法 七.六种查找算法的时间复杂度 一.顺序查找算法 顺序查找又称为线性查找,是最简单的查找算法.这种算法就是按照数据的顺序一项一项逐个查找,所以不管数据顺序如何,都得从头到尾地遍历一次.顺序查找的优点就是数据在查找前,不需要对其进行任何处理(包括排序).缺点是查找速度慢,如果数据列的第一个数据就是想要查找的数据,则该算法查找速度为最快,只需查找一次即可:如果查找的数据是数据列的最后一

  • Java实现查找算法的示例代码(二分查找、插值查找、斐波那契查找)

    Java实现查找算法的示例代码(二分查找、插值查找、斐波那契查找)

    目录 1.查找概述 2.顺序查找 3.二分查找 3.1 二分查找概述 3.2 二分查找实现 4.插值查找 4.1 插值查找概述 4.2 插值查找实现 5.斐波那契查找 5.1 斐波那契查找概述 5.2 斐波那契查找实现 5.3 总结 1.查找概述 查找表: 所有需要被查的数据所在的集合,我们给它一个统称叫查找表.查找表(Search Table)是由同一类型的数据元素(或记录)构成的集合. 查找(Searching): 根据给定的某个值,在查找表中确定一个其关键字等于给定值的数据元素(或记录).

  • Java实现的两种常见简单查找算法示例【快速查找与二分查找】

    本文实例讲述了Java实现的两种常见简单查找算法.分享给大家供大家参考,具体如下: 前言: 查找是指从一批记录当中找出满足制定条件的某一记录的过程. 在平常的程序的编写当中很多时候时用得上的,这里简单介绍两个查找算法 1. 快速查找: 这个是相当简单的,以数组举例,就用一个for循环去查找数组中需要查找的数据 例子: public static boolean quickSearch(int a[], int x) { boolean f = false; int length = a.leng

随机推荐