python深度总结线性回归
目录
- 概述
- 例子
- 通俗解释
- 数学推导
- 误差
- 评估方法
- 梯度下降
- 批量梯度下降
- 随机梯度下降
- 小批量梯度下降法
- 案例一
概述
线性回归的定义是: 目标值预期是输入变量的线性组合. 线性模型形式简单, 易于建模, 但却蕴含着机器学习中一些重要的基本思想. 线性回归, 是利用数理统计中回归分析, 来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法, 运用十分广泛.
优点: 结果易于理解, 计算不复杂
缺点: 对非线性的数据拟合不好
例子
数据: 工资和年龄 (2 个特征)
目标: 预测银行会贷款给我多少钱 (标签)
| 工资 | 年龄 | 额度 |
| 4000 | 25 | 20000 |
| 8000 | 30 | 70000 |
| 5000 | 28 | 35000 |
| 7500 | 33 | 50000 |
| 12000 | 40 | 85000 |
工资和年龄都会影响最终银行贷款的结果. 那么它们各自有多大的影响呢?
通俗解释
X1, X2 代表我们的两个特征: 年龄和工资. Y 代表银行最终会借给我们多少钱.
找到最合适的一条线 (想象一个高维 ) 来最好的拟合我们的数据点. 如下图所示:
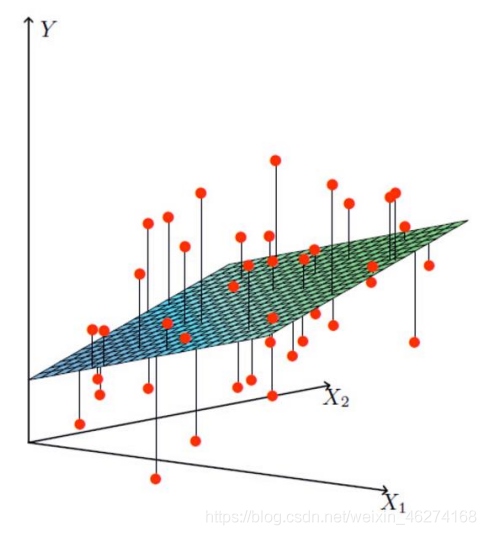
数学推导
假设 θ1 代表年龄的参数, θ2 代表工资的参数, 那么:
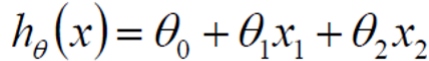
注: θ0 为偏置顶, 相当于 C
线性模型, 中的向量 θ 值. 客观的表达了各属性在预测中的重要性, 因此线性模型有很好的解释性. 对于这种 “多特征预测” 也就是 (多元线性回归), 那么线性回归就是在这个基础上得到这些 θ 的值. 然后以这些值来建立模型, 预测试数据. 简单的来说就是学得一个线性模型以尽可能准确的预测实际输出标记.
那么如果对于多变量线性回归来说我们可以通过向量的方式来表示 θ 值与特征 X 值之间的关系:
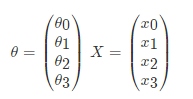
两向量相乘, 结果为一个整数是估计值. 其中所有特征集合的第一个特征值 x0=1, 那么我们可以通过通用的向量公式来表示性模型:
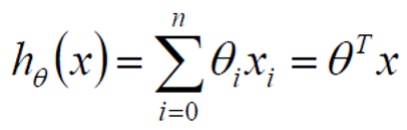
误差
真实值和预测值之间肯定是要存在差异的. 对于每个样本:
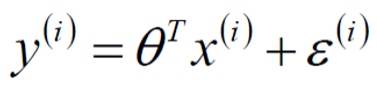
注: ε 代表误差
误差ε^(i)是独立并且具有相同的分布, 并且服从均值为 0 方差为θ^2的正态分布 (normal distribution).
独立: 凹凸曼和马保国一起来贷款, 不可能因为马保国贷款了 30 个亿, 就少给凹凸曼钱.
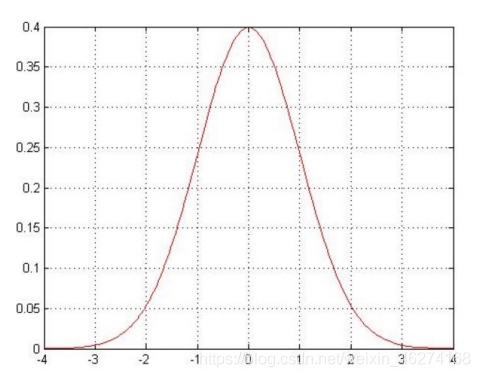
预测值与误差:
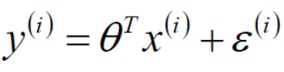
误差服从高斯分布:
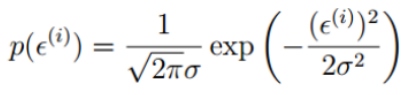
将 1 式带入 2 式:
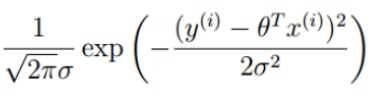
似然函数:
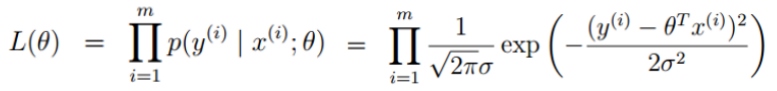
对数似然函数:
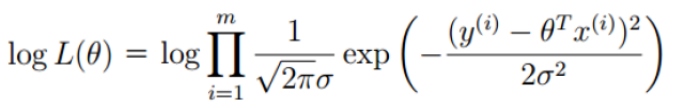
简化:
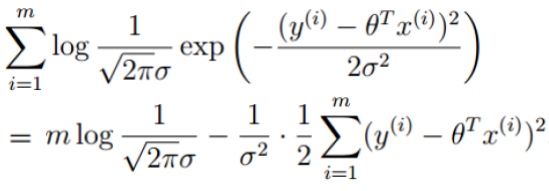
让似然函数越大越好 (最小二乘法):
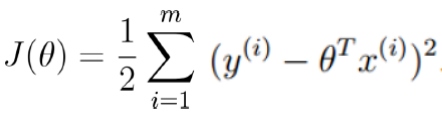
目标函数:
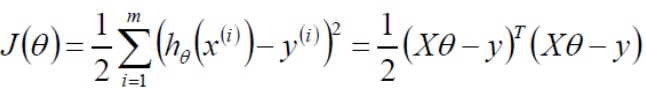
求偏导:
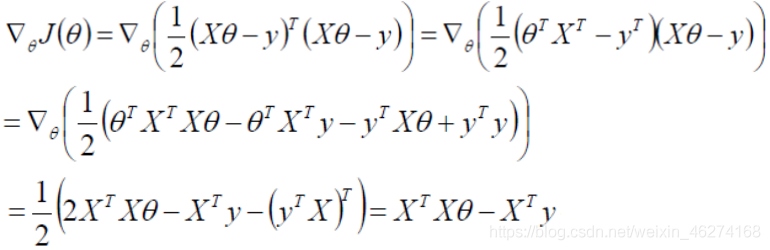
偏导等于 0:
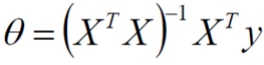
评估方法
最常用的评估项 R^2:

R^2 的取值越接近于 1 我们认为模型拟合的越好.
梯度下降
上面误差公式是一个通式, 我们取两个单个变量来求最小值. 目标函数:
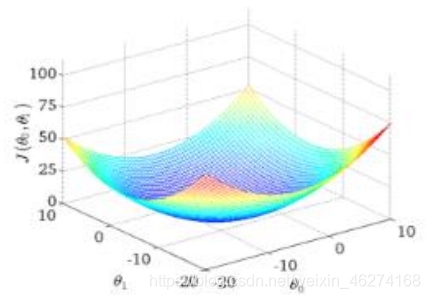
寻找山谷的最低点, 也就是我们的目标函数终点 (什么样的参数能使得目标函数达到极值点)
下山分几步走呢?
找到当前最合适的方向走一小步按照方向与步伐去更新我们的参数
目标函数:
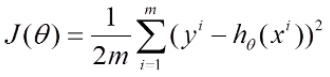
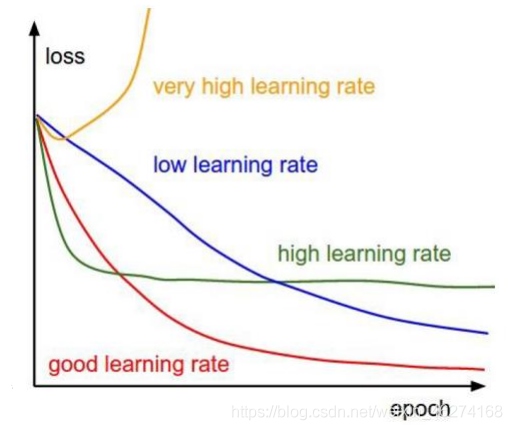
学习率 (learning_rate): 对结果影响较大, 越小越好.
数据批次 (batch_size): 优先考虑内存和效率, 批次大小是次要的.
批量梯度下降
目标
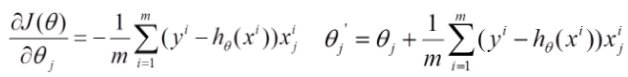
容易得到最优解, 但是由于每次考虑所有样本, 速度很慢.
随机梯度下降
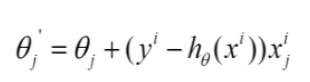
每次找一个样本, 迭代速度快, 但不一定每次都朝着收敛的反向.
小批量梯度下降法

案例一
波士顿房价预测
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression, SGDRegressor
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
def mylinear():
"""
线性回归直接预测房子价格
:return: None
"""
# 获取数据
lb = load_boston()
# 分割数据记到训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)
# 进行标准化处理, 目标值处理
# 特征值和目标是都必须进行标准化处理, 实例化两个标准化API
std_x = StandardScaler()
x_train = std_x.fit_transform(x_train)
x_test = std_x.fit_transform(x_test)
# 目标值
std_y = StandardScaler()
y_train = std_y.fit_transform(y_train.reshape(-1, 1))
y_test = std_y.fit_transform(y_test.reshape(-1, 1))
# estimator预测
# 正规方程求解方式预测结果
lr = LinearRegression()
lr.fit(x_train, y_train)
print(lr.coef_)
# 预测测试集房子价格
y_lr_predict = std_y.inverse_transform(lr.predict(x_test))
print("正规方程式测试集里面每个房子的预测价格: ", y_lr_predict)
print("正规方程的均方误差: ", mean_squared_error(std_y.inverse_transform(y_test), y_lr_predict))
# 梯度下降去进行房价预测
sgd = SGDRegressor()
sgd.fit(x_train, y_train)
print(sgd.coef_)
# 预测测试集的房子价格
y_sgd_predict = std_y.inverse_transform(sgd.predict(x_test))
print("梯度下降式测试集里面每个房子的预测价格: ", y_sgd_predict)
print("梯度下降的均方误差: ", mean_squared_error(std_y.inverse_transform(y_test), y_sgd_predict))
return None
if __name__ == "__main__":
mylinear()
输出结果:
[[-0.12225698 0.12791281 -0.00206122 0.05700013 -0.2608399 0.28139416
0.01481249 -0.33807474 0.3299154 -0.23182836 -0.21123181 0.09206512
-0.39973041]]
正规方程式测试集里面每个房子的预测价格: [[28.95666718]
[25.61614205]
[24.20558764]
[19.30978406]
[35.89982059]
[29.03187299]
[26.34111014]
[19.46710495]
[20.6689787 ]
[29.93653292]
[25.11165216]
[32.91673513]
[19.84546548]
[23.5563843 ]
[21.79474763]
[15.75074992]
[19.80615694]
[12.98286759]
[27.59995691]
[19.00192788]
[36.16248095]
[19.2767701 ]
[16.52561836]
[23.05284655]
[16.59241324]
[25.66405442]
[30.7677223 ]
[19.86797053]
[ 9.39422797]
[27.10530759]
[27.17712717]
[39.44877655]
[10.03000383]
[15.42825832]
[23.13702928]
[14.52254261]
[19.38595173]
[29.06816506]
[36.30187936]
[22.5685246 ]
[ 9.88826283]
[21.33573342]
[31.3551175 ]
[16.18170604]
[27.59483437]
[31.66145736]
[14.31706514]
[24.46295319]
[17.51893204]
[19.35269608]
[24.26523283]
[24.86190305]
[25.11947262]
[28.93202524]
[15.75107827]
[13.3417495 ]
[22.59649735]
[29.00114487]
[12.20666867]
[30.63609004]
[21.96199386]
[27.06032461]
[25.1791211 ]
[17.97595194]
[41.57497749]
[21.43625394]
[24.28803424]
[16.5167138 ]
[19.38589021]
[ 8.06164985]
[23.7550887 ]
[12.10636177]
[23.67230518]
[31.52266655]
[19.30684626]
[20.31342004]
[25.13624205]
[18.6725454 ]
[34.44267213]
[19.76331507]
[33.68001958]
[17.21843608]
[11.93697393]
[20.10130687]
[20.60069168]
[33.02551169]
[12.20848437]
[11.34921413]
[36.81923651]
[43.09091788]
[24.5904135 ]
[27.19519096]
[13.42695648]
[21.31070858]
[18.78980458]
[26.7739455 ]
[21.04064808]
[19.37399749]
[20.61932093]
[12.70789542]
[27.30728839]
[29.19812469]
[18.2215341 ]
[14.88442393]
[13.08985585]
[37.26784993]
[23.0054703 ]
[45.03638993]
[24.43103986]
[ 9.70593527]
[ 7.20755399]
[24.11659246]
[16.87989582]
[23.8839 ]
[36.74286927]
[17.52801739]
[21.14217981]
[ 8.33442145]
[20.77366903]
[25.11687425]
[34.79817667]
[17.48069049]
[ 7.79217297]
[21.46168783]
[12.12750804]
[23.37886385]
[13.03642996]]
正规方程的均方误差: 19.228239448103142
[-0.10382102 0.09549223 -0.0575206 0.06192685 -0.17919477 0.31416038
-0.0060828 -0.2718829 0.16557575 -0.09171927 -0.19702721 0.09358103
-0.38969764]
梯度下降式测试集里面每个房子的预测价格: [28.32281003 25.30899723 24.37354695 19.81132568 35.86134383 29.54339861
26.40901657 19.91790232 21.08280077 30.8745518 25.04025974 32.61880171
20.06776623 23.27211209 21.49391276 15.07364423 19.3604463 13.24307268
27.91816594 18.46564888 36.5121198 18.60090036 17.07584378 23.61453885
15.44119731 26.55848283 30.95932966 20.48910926 8.92774087 25.64122283
26.5405097 39.56312391 9.60876044 16.194631 21.86126606 14.3384503
19.6672515 28.37094255 37.13748452 22.56961348 10.95474568 21.31897902
31.99623025 16.32155785 27.56422641 31.91738771 16.07941322 25.21406318
17.07667764 18.61941274 23.61541029 25.09956295 24.16633871 29.24889477
16.17014144 13.52204965 21.76470038 28.75088192 11.39083277 29.94854783
21.97184713 26.76638021 25.37366415 17.75713168 42.17712979 21.44617697
24.65166416 15.74898705 19.28498974 7.18254411 23.64316345 12.17079475
23.22062874 30.81709679 19.39958374 20.53408606 25.34565728 18.55272456
33.84685681 19.4801645 33.86657711 17.02691146 11.07262797 20.44699002
20.83170047 32.66795247 11.2561216 11.94847677 35.85096014 42.30377951
24.56324407 27.96815655 13.30901928 22.23063794 19.1259557 27.02051826
21.39186325 20.33181273 21.29435341 11.25823767 27.67529642 30.095733
18.76124598 13.85728059 14.68490838 37.53663617 22.46940546 45.09885288
24.49884024 10.51414764 7.91453997 23.66015594 17.30342205 24.23971059
36.76137912 16.98059079 21.46394599 7.28066947 20.76359414 24.55927982
35.63307238 16.9695351 7.33008978 21.71197098 12.31280728 22.41710171
13.31011409]
梯度下降的均方误差: 19.28139772207173
到此这篇关于python深度总结线性回归的文章就介绍到这了,更多相关python线性回归内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们!

