python实现数学模型(插值、拟合和微分方程)

问题1 车辆数量估计

题目描述

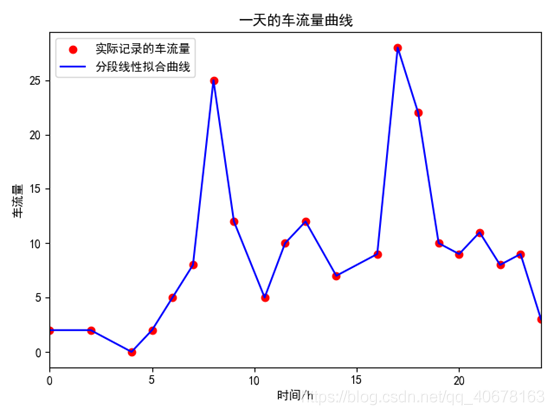
交通管理部门为了掌握一座桥梁的通行情况，在桥梁的一端每隔一段不等的时间，连续记录1min内通过桥梁的车辆数量，连续观测一天24h的通过车辆，车辆数据如下表所示。试建立模型分析估计这一天中总共有多少车辆通过这座桥梁。

python 实现(关键程序)

def get_line(xn, yn):
    def line(x):
        index = -1
        # 找出x所在的区间
        for i in range(1, len(xn)):
            if x <= xn[i]:
                index = i - 1
                break
            else:
                i += 1
        if index == -1:
            return -100
        # 插值
        result = (x - xn[index + 1]) * yn[index] / float((xn[index] - xn[index + 1])) + (x - xn[index]) * yn[
            index + 1] / float((xn[index + 1] - xn[index]))
        return result
    return line
time = [0, 2, 4, 5, 6, 7, 8,
    9, 10.5, 11.5, 12.5, 14, 16, 17,
    18, 19, 20, 21, 22, 23, 24]
num = [2, 2, 0, 2, 5, 8, 25,
    12, 5, 10, 12, 7, 9, 28,
    22, 10, 9, 11, 8, 9, 3]
# 分段线性插值函数
lin = get_line(time, num)
# time_n = np.arange(0, 24, 1/60)
time_n = np.linspace(0, 24, 24*60+1)
num_n = [lin(i) for i in time_n]
sum_num = sum(num_n)
print("估计一天通过的车辆：%d" % sum_num)

结果

问题2 旧车平均价格

题目描述

某年美国旧车价格的调查资料如下表所示，其中 x i x_i xi​表示轿车的使用年数， y i y_i yi​表示相应的平均价格。试分析用什么形式的曲线拟合表中所给的数据，并预测使用4.5年后轿车的平均价格大致为多少?

Python 实现(关键程序)

from scipy.optimize import curve_fit
def func(x, a, b, c): # 指数函数拟合
  return a * (b**(x-1)) + c

year = np.arange(1, 11, 1)
price = [2615, 1943, 1494, 1087, 765, 538, 484, 290, 226, 204]

popt, pcov = curve_fit(func, year, price)
a = popt[0]
b = popt[1]
c = popt[2]
price_fit = func(year, a, b, c)

结果

问题3 微分方程组求解

题目描述

求下列微分方程组(竖直加热板的自然对流)的数值解

Python实现(关键程序)

from scipy.integrate import solve_ivp
def natural_convection(eta, y): # 将含有两个未知函数的高阶微分方程降阶，得到由2+3个一阶微分方程组成的方程组
  T1 = y[0]
  T2 = y[1]
  f1 = y[2]
  f2 = y[3]
  f3 = y[4]
  return T2, -2.1*f1*T2, f2, f3, -3*f1*f3 + 2*(f2**2)-T1

eta = np.linspace(0, 10, 1000)
eta_span = [0, 10]
init = np.array([ 1, -0.5, 0, 0, 0.68])

curve = solve_ivp(natural_convection, eta_span, init, t_eval=eta)

结果

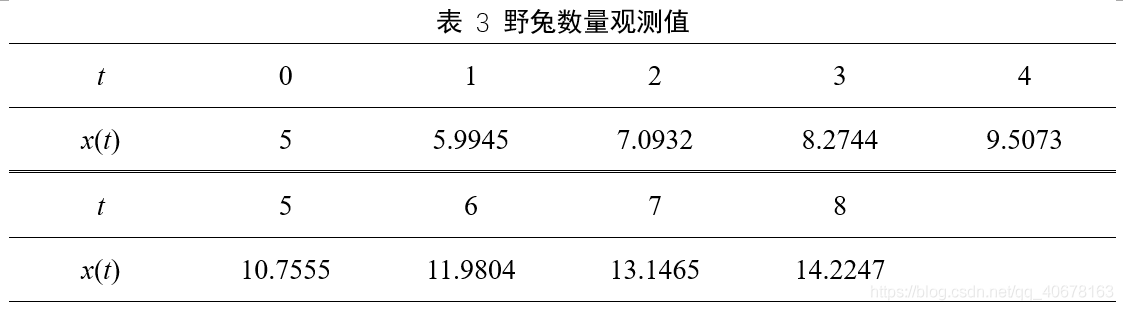
问题4 野兔数量 题目描述

某地区野兔的数量连续9年的统计数量(单位:十万)如下表所示.预测t = 9, 10时野兔的数量。

Python实现(关键程序)

import numpy as np

year = np.arange(0, 9, 1)
num = [5, 5.9945, 7.0932, 8.2744, 9.5073, 10.7555, 11.9804, 13.1465, 14.2247]

fit = np.polyfit(year, num, 1)
print("线性拟合表达式：", np.poly1d(fit))
num_fit = np.polyval(fit, year)
plt.plot(year, num, 'ro', label='原始数据')
plt.plot(year, num_fit, 'b-',label='拟合曲线')
year_later = np.arange(8, 11, 0.5)
num_fit_curve = fit[0] * year_later + fit[1]

结果

到此这篇关于python实现数学模型(插值、拟合和微分方程)的文章就介绍到这了,更多相关python数学模型内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！