R语言时间序列TAR阈值自回归模型示例详解

为了方便起见，这些模型通常简称为TAR模型。这些模型捕获了线性时间序列模型无法捕获的行为，例如周期，幅度相关的频率和跳跃现象。Tong和Lim（1980）使用阈值模型表明，该模型能够发现黑子数据出现的不对称周期性行为。

一阶TAR模型的示例：

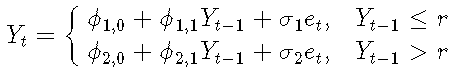
σ是噪声标准偏差，Yt-1是阈值变量，r是阈值参数， {et}是具有零均值和单位方差的iid随机变量序列。

每个线性子模型都称为一个机制。上面是两个机制的模型。

考虑以下简单的一阶TAR模型：

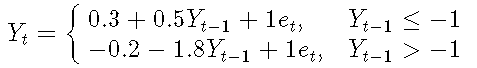
#低机制参数

i1 = 0.3
p1 = 0.5
s1 = 1

#高机制参数

i2 = -0.2
p2 = -1.8
s2 = 1

thresh = -1
delay = 1

#模拟数据
y=sim(n=100,Phi1=c(i1,p1),Phi2=c(i2,p2),p=1,d=delay,sigma1=s1,thd=thresh,sigma2=s2)$y

#绘制数据

plot(y=y,x=1:length(y),type='o',xlab='t',ylab=expression(Y[t])
abline(thresh,0,col="red")

TAR模型框架是原始TAR模型的修改版本。它是通过抑制噪声项和截距并将阈值设置为0来获得的：

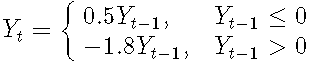
框架的稳定性以及某些规律性条件意味着TAR的平稳性。稳定性可以理解为，对于任何初始值Y1，框架都是有界过程。

在[164]中：

#使用不同的起点检查稳定性
startvals = c(-2, -1.1,-0.5, 0.8, 1.2, 3.4)

count = 1
for (s in startvals) {
	ysk[1
		} else {
			ysk[i] = -1.8*ysk[i-1]
		}

	count = count + 1
}

#绘制不同实现
matplot(t(x),type="l"
abline(0,0)

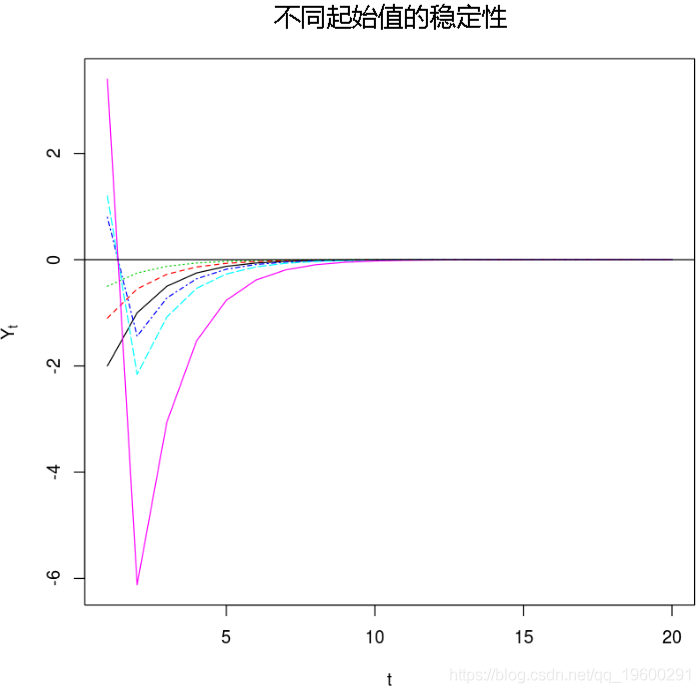
Chan和Tong（1985）证明，如果满足以下条件，则一阶TAR模型是平稳的

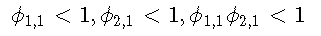
一般的两机制模型写为：

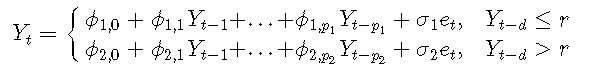
在这种情况下，稳定性更加复杂。然而，Chan and Tong（1985）证明，如果

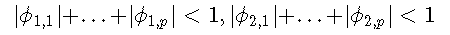
模型估计

一种方法以及此处讨论的方法是条件最小二乘（CLS）方法。

为简单起见，除了假设p1 = p2 = p，1≤d≤p，还假设σ1=σ2=σ。然后可以将TAR模型方便地写为

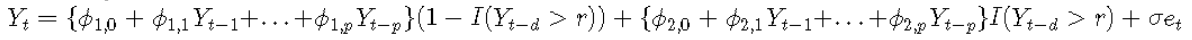
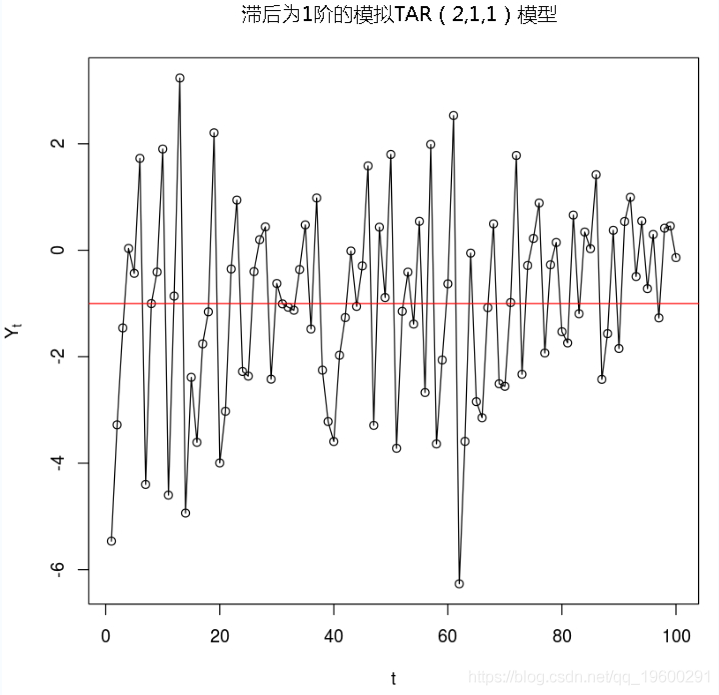
如果Yt-d> r，则I（Yt-d> r）= 1，否则为0。CLS最小化条件残差平方和：

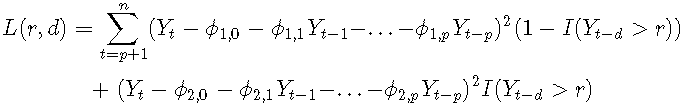
在这种情况下，可以根据是否Yt-d≤r将数据分为两部分，然后执行OLS估计每个线性子模型的参数。

如果r未知。

在r值范围内进行搜索，该值必须在时间序列的最小值和最大值之间，以确保该序列实际上超过阈值。然后从搜索中排除最高和最低10％的值

在此受限频带内，针对不同的r = yt值估算TAR模型。选择r的值，使对应的回归模型的残差平方和最小。

#找到分位数
lq = quantile(y,0.10)
uq = quantile(y,0.90)

#绘制数据
plot(y=y,x=1:length(y),type='o',xlab='t'abline(lq,0,col="blue")
abline(uq,0,col="blue")

#模型估计数

sum( (lq <= y ) & (y <= uq) )

80

如果d未知。

令d取值为1,2,3，...，p。为每个d的潜在值估算TAR模型，然后选择残差平方和最小的模型。

Chan（1993）已证明，CLS方法是一致的。

最小AIC（MAIC）方法

由于在实践中这两种情况的AR阶数是未知的，因此需要一种允许对它们进行估计的方法。对于TAR模型，对于固定的r和d，AIC变为

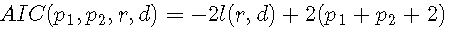
然后，通过最小化AIC对象来估计参数，以便在某个时间间隔内搜索阈值参数，以使任何方案都有足够的数据进行估计。

#估算模型
#如果知道阈值

#如果阈值尚不清楚

#MAIC 方法

for (d in 1:3) {
	if (model.tar.s$AIC < AIC.best) {
		AIC.best = model.tar.s$AIC
		model.best$d = d
		model.best$p1 = model.tar.s
ar.s$AIC, signif(model.tar.s$thd,4)

AICM

d	AIC	R	1	2
1	311.2	-1.0020	1	1
2	372.6	0.2218	1	2
3	388.4	-1.3870	1	0

非线性测试

1.使用滞后回归图进行目测。

绘制Yt与其滞后。拟合的回归曲线不是很直，可能表明存在非线性关系。

在[168]中：

lagplot(y)

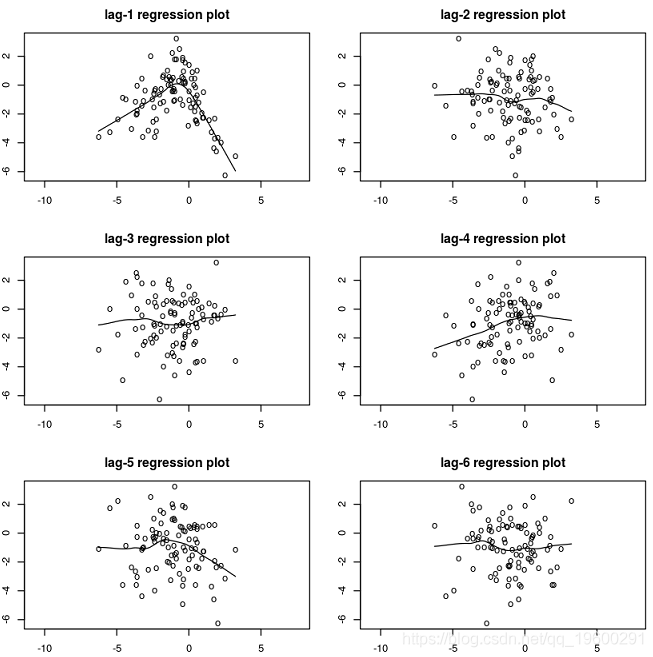
2.Keenan检验：

考虑以下由二阶Volterra展开引起的模型：

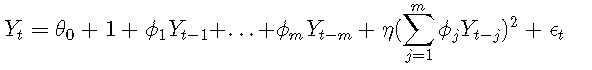
其中{ϵt} 的iid正态分布为零均值和有限方差。如果η=0，则该模型成为AR（mm）模型。

可以证明，Keenan检验等同于回归模型中检验η=0：

其中Yt ^ 是从Yt-1，...，Yt-m上的Yt回归得到的拟合值。

3. Tsay检验：

Keenan测试的一种更通用的替代方法。用更复杂的表达式替换为Keenan检验给出的上述模型中的项η（∑mj = 1ϕjYt-j）2。最后对所有非线性项是否均为零的二次回归模型执行F检验。

在[169]中：

#检查非线性: Keenan, Tsay
#Null is an AR model of order 1
Keenan.test(y,1)

$test.stat

90.2589565661567

$p.value

1.76111433596097e-15

$order

1

在[170]中：

Tsay.test(y,1)

$test.stat

71.34

$p.value

3.201e-13

$order

1

4.检验阈值非线性

这是基于似然比的测试。

零假设是AR（pp）模型；另一种假设是具有恒定噪声方差的p阶的两区域TAR模型，即σ1=σ2=σ。使用这些假设，可以将通用模型重写为

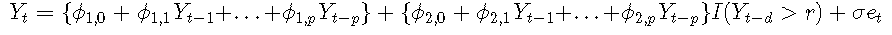
零假设表明ϕ2,0 = ϕ2,1 = ... = ϕ2，p = 0。

似然比检验统计量可以证明等于

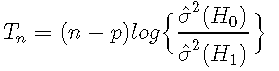
其中n-p是有效样本大小，σ^ 2（H0）是线性AR（p）拟合的噪声方差的MLE，而σ^ 2（H1）来自TAR的噪声方差与在某个有限间隔内搜索到的阈值的MLE。

H0下似然比检验的采样分布具有非标准采样分布；参见Chan（1991）和Tong（1990）。

在[171]中：

res = tlrt(y, p=1, d=1, a=0.15, b=0.85)
res

$percentiles

14.1

85.9
$test.statistic

: 142.291963130459

$p.value

: 0

模型诊断

使用残差分析完成模型诊断。TAR模型的残差定义为

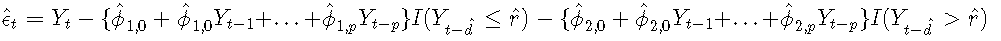
标准化残差是通过适当的标准偏差标准化的原始残差：

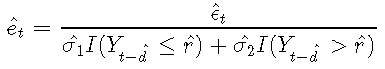
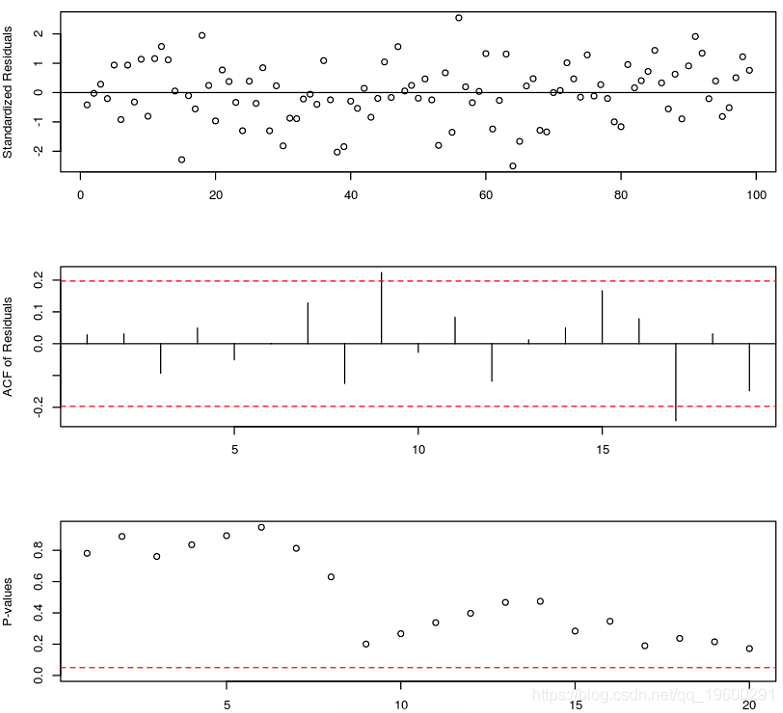
如果TAR模型是真正的数据机制，则标准化残差图应看起来是随机的。可以通过检查标准化残差的样本ACF来检查标准化误差的独立性假设。

#模型诊断

diag(model.tar.best, gof.lag=20)

预测

预测分布通常是非正态的。通常，采用模拟方法进行预测。考虑模型

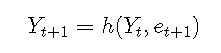
然后给定Yt = yt，Yt-1 = yt-1，...

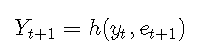
因此，可以通过从误差分布中绘制et + 1并计算h（yt，et + 1），来获得单步预测分布的Yt + 1的实现。 。

通过独立重复此过程 B 次，您可以 从向前一步预测分布中随机获得B值样本 。

可以通过这些B 值的样本平均值来估计提前一步的预测平均值 。

通过迭代，可以轻松地将仿真方法扩展为找到任何l步提前预测分布：

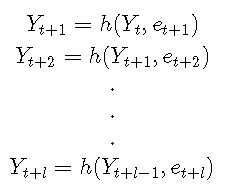
其中Yt = yt和et + 1，et + 2，...，et + l是从误差分布得出的ll值的随机样本。

在[173]中：

#预测
model.tar.pred r.best, n.ahead = 10, n.sim=1000)
y.pred = ts(c
lines(ts(model.tar.pred$pred.interval[2,], start=end(y) + c(0,1), freq=1), lty=2)
lines(ts(model

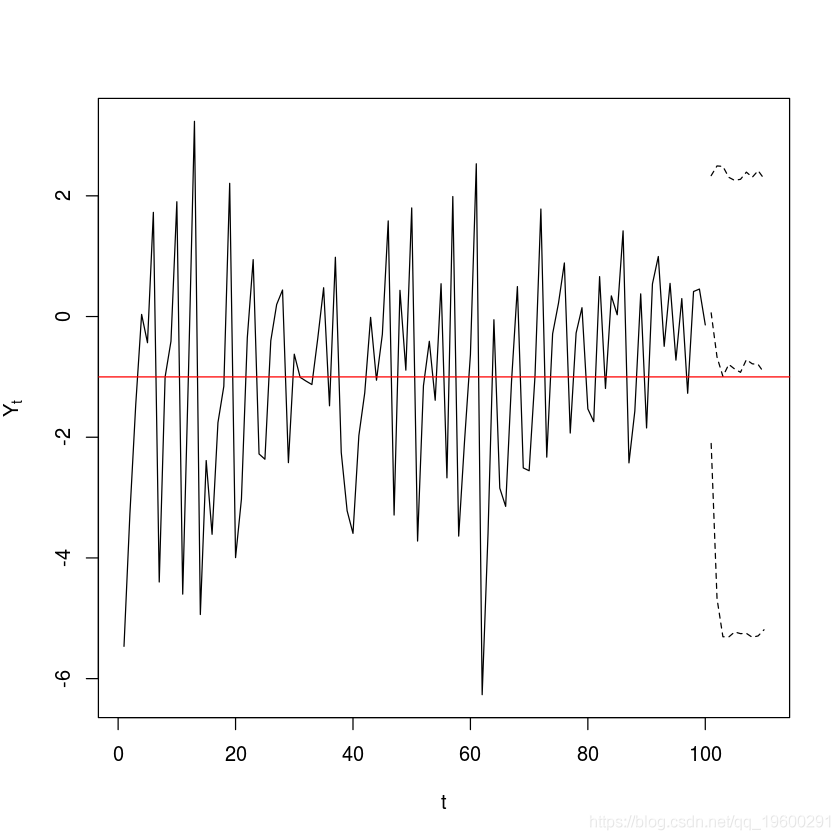
样例

这里模拟的时间序列是1700年至1988年太阳黑子的年数量。

在[174]中：

#数据集
#太阳黑子序列，每年

plot.ts(sunsp

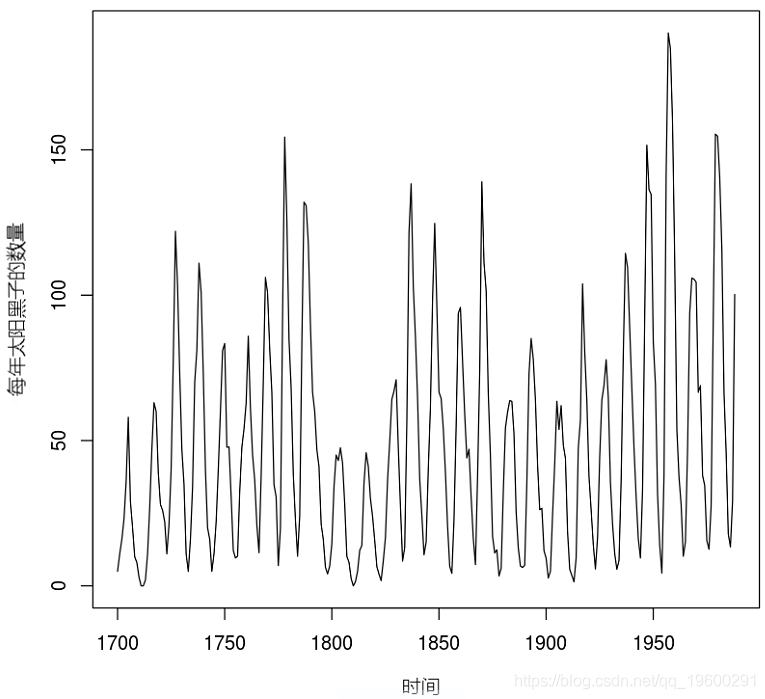
#通过滞后回归图检查非线性
lagplot(sunspo)

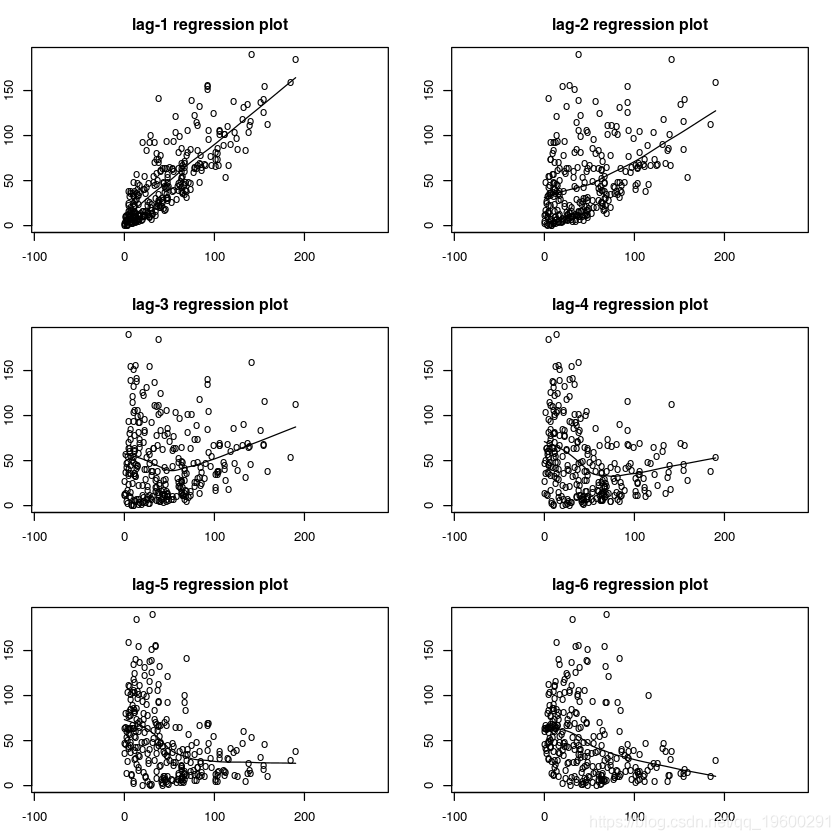
#使用假设检验检查线性
Keenan.test(sunspot.year)
Tsay.test(sunspot.year)

$test.stat

18.2840758932705

$p.value

2.64565849317573e-05

$order

9

$test.stat

3.904

$p.value

6.689e-12

$order

9

在[177]中：

#使用MAIC方法
AIC{
	sunspot.tar.s = tar(sunspot.year, p1 = 9, p2 = 9, d = d, a=0.15, b=0.85)

AICM

d	AIC	R	1	2
1	2285	22.7	6	9
2	2248	41.0	9	9
3	2226	31.5	7	9
4	2251	47.8	8	7
5	2296	84.8	9	3
6	2291	19.8	8	9
7	2272	43.9	9	9
8	2244	48.5	9	2
9	2221	47.5	9	3

在[178]中：

#测试阈值非线性
tl(sunspot.year, p=9, d=9, a=0.15, b=0.85)

$percentiles

15

85
$test.statistic

: 52.2571950943405

$p.value

: 6.8337179274236e-06

#模型诊断
tsdiag(sunspot.tar.best)

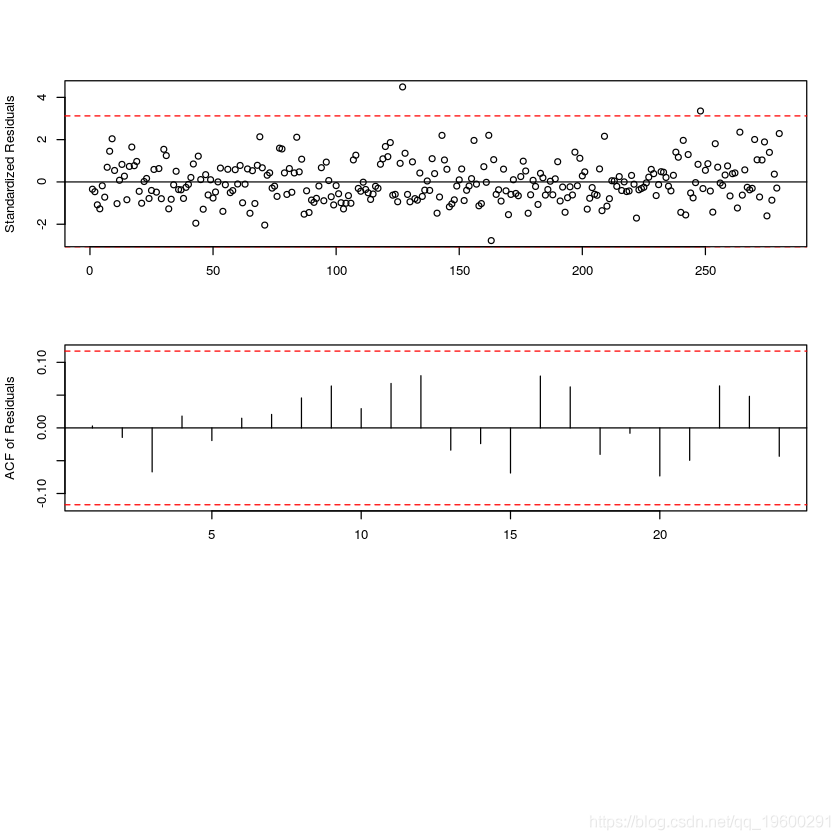
#预测
sunspot.tar.pred <- predict(sunspot.tar.best, n.ahead = 10, n.sim=1000)

lines(ts(sunspot.tar.pred$pretart=e

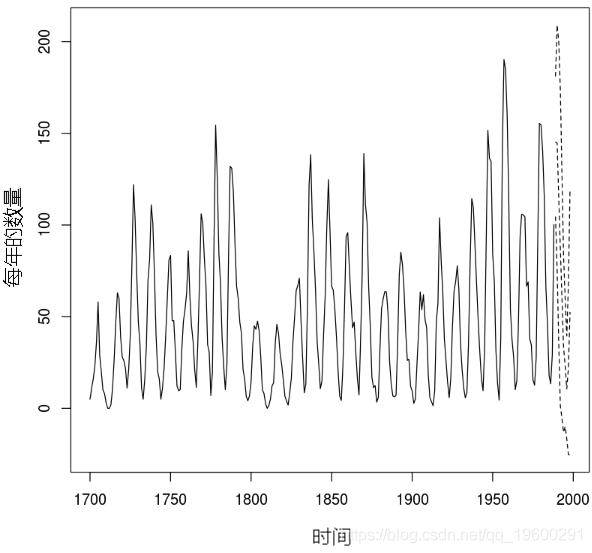
#拟合线性AR模型
#pacf(sunspot.year)
#尝试AR阶数9
ord = 9
ar.mod <- arima(sunspot.year, order=c(ord,0,0), method="CSS-ML")

plot.ts(sunspot.year[10:289]

模拟TAR模型上的AR性能

示例1. 将AR（4）拟合到TAR模型

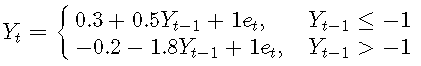
set.seed(12349)
#低机制参数
i1 = 0.3
p1 = 0.5
s1 = 1

#高机制参数
i2 = -0.2
p2 = -1.8
s2 = 1

thresh = -1
delay = 1

nobs = 200
#模拟200个样本
y=sim(n=nobs,Phi1=c(i1,p1),Phi$y

#使用Tsay的检验确定最佳AR阶数
ord <- Tsay.test(y)$order
#线性AR模型
#pacf(sunspot.year)
#try AR order 4

例子2. 将AR（4）拟合到TAR模型

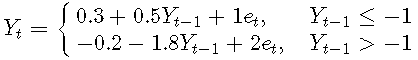
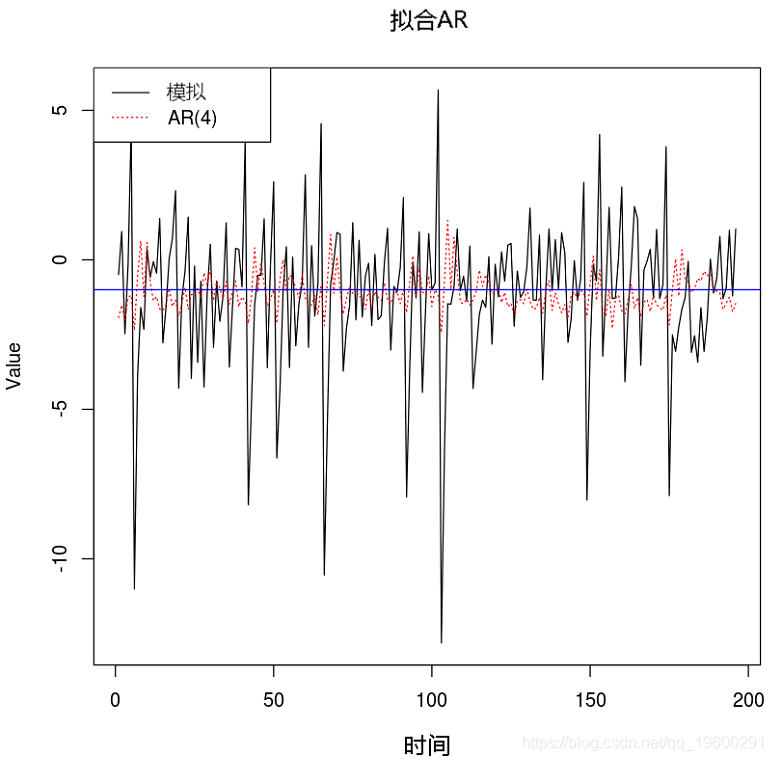
例子3. 将AR（3）拟合到TAR模型

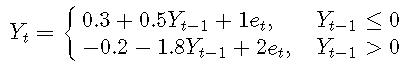
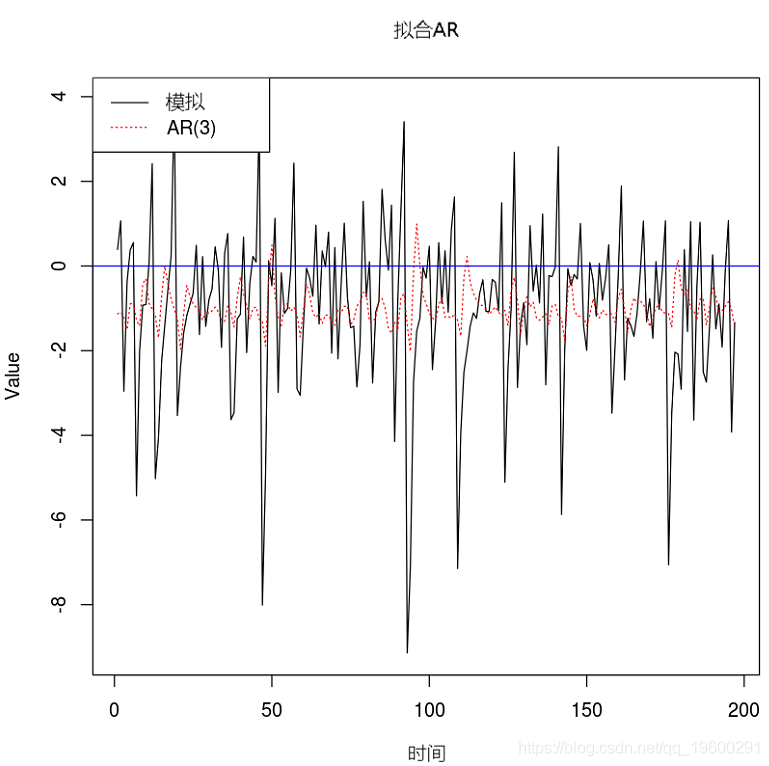
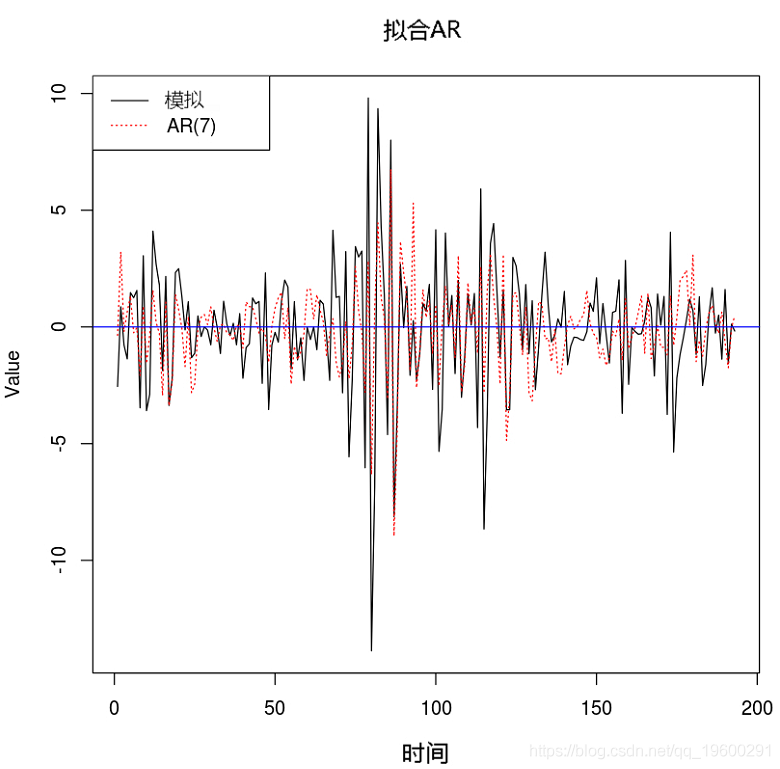
例子3. 将AR（7）拟合到TAR模型

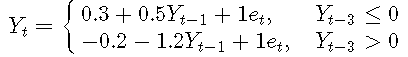
参考文献

恩德斯（W. Enders），2010年。应用计量经济学时间序列

---

到此这篇关于R语言时间序列TAR阈值自回归模型示例详解的文章就介绍到这了,更多相关R语言时间序列内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！