Python深度学习pytorch神经网络Dropout应用详解解

目录
  • 扰动的鲁棒性
  • 实践中的dropout
  • 简洁实现

扰动的鲁棒性

在之前我们讨论权重衰减（L2​正则化）时看到的那样，参数的范数也代表了一种有用的简单性度量。简单性的另一个有用角度是平滑性，即函数不应该对其输入的微笑变化敏感。例如，当我们对图像进行分类时，我们预计向像素添加一些随机噪声应该是基本无影响的。

dropout在正向传播过程中，计算每一内部层同时注入噪声，这已经成为训练神经网络的标准技术。这种方法之所以被称为dropout，因为我们从表面上看是在训练过程中丢弃（drop out）一些神经元。在整个训练过程的每一次迭代中，dropout包括在计算下一层之前将当前层中的一些节点置零。

那么关键的挑战就是如何注入这种噪声，一种想法是以一种无偏的方式注入噪声。这样在固定住其他层时，每一层的期望值等于没有噪音时的值。

实践中的dropout

之前多层感知机是带有一个隐藏层和5个隐藏单元的。当我们将dropout应用到隐藏层时，以 p的概率将隐藏单元置为零时，结果可以看作是一个只包含原始神经元子集的网络。右图中，删除了  h2​和  h5​。因此，输出的计算不再依赖于 h2​或  h5​，并且它们各自的梯度在执行反向传播时也会消失。这样，输出层的计算不能过度依赖于 h1​,…,h5​的任何一个元素。

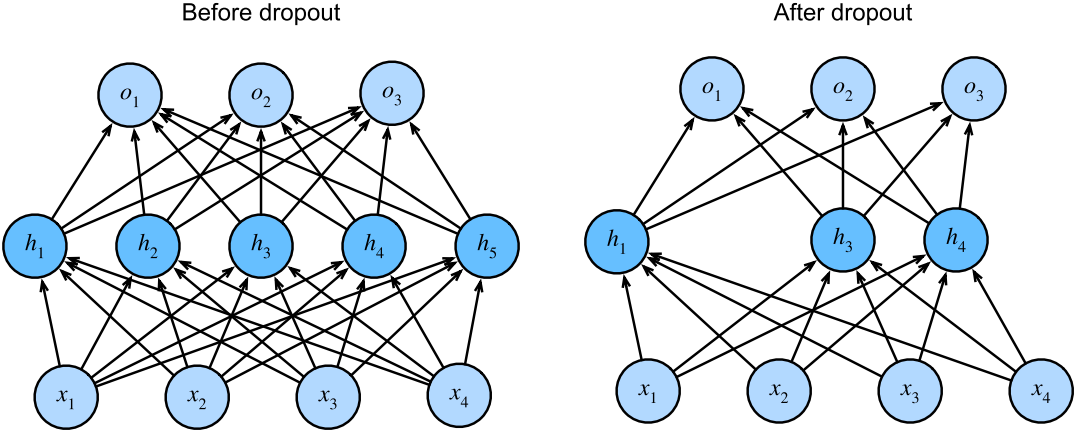
通常，我们在测试时仅用dropout。给定一个训练好的模型和一个新的样本，我们不会丢弃任何节点，因此不需要标准化。

简洁实现

对于高级API，我们所需要做的就是在每个全连接层之后添加一个Dropout层，将丢弃概率作为唯一的参数传递给它的构造函数。在训练过程中，Dropout层将根据指定的丢弃概率随机丢弃上一层的输出（相当于下一层的输入）。当不处于训练模式时，Dropout层仅在测试时传递数据。

net = nn.Sequential(nn.Flatten(),
					nn.Linear(784, 256),
					nn.ReLU(),
					# 在第一个全连接层之后添加一个dropout层
					nn.Dropout(dropout1),
					nn.Linear(256, 256),
					nn.ReLU(),
					# 在第二个全连接层之后添加一个dropout层
					nn.Dropout(dropout2),
					nn.Linear(256, 10))

def init_weights(m):
	if type(m) == nn.Linear:
		nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights)

接下来，我们对模型进行训练和测试。

trainer = torch.optim.SGD(net.parameters(), lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

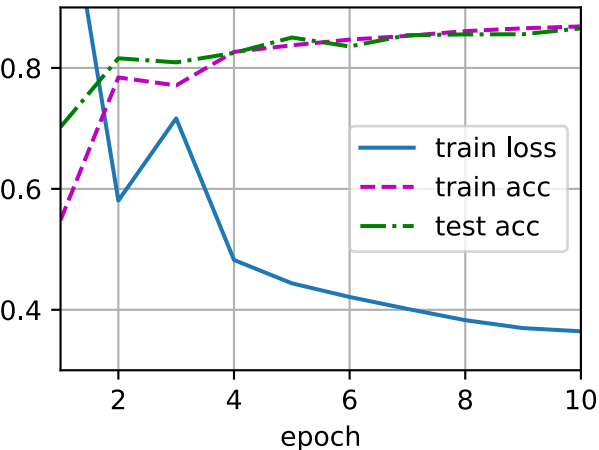
以上就是Python深度学习pytorch神经网络Dropout应用详解解的详细内容，更多关于pytorch神经网络Dropout应用的资料请关注我们其它相关文章！

赞 (0)

相关推荐

  • PyTorch 实现L2正则化以及Dropout的操作

    PyTorch 实现L2正则化以及Dropout的操作

    了解知道Dropout原理 如果要提高神经网络的表达或分类能力,最直接的方法就是采用更深的网络和更多的神经元,复杂的网络也意味着更加容易过拟合. 于是就有了Dropout,大部分实验表明其具有一定的防止过拟合的能力. 用代码实现Dropout Dropout的numpy实现 PyTorch中实现dropout import torch.nn.functional as F import torch.nn.init as init import torch from torch.autograd

  • 浅谈pytorch中的dropout的概率p

    最近需要训练一个模型,在优化模型时用了dropout函数,为了减少过拟合. 训练的时候用dropout,测试的时候不用dropout.刚开始以为p是保留神经元的比率,训练设置0.5,测试设置1,loss根本没减小过,全设置成1也是一样的效果,后来就考虑到是不是p设置错了. 上网一搜,果然是的!!!p的含义理解错了!不是保留的,而是不保留的! 具体的代码为: x2 = F.dropout(x1, p) x1是上一层网络的输出,p是需要删除的神经元的比例. 当p=0时,保留全部神经元更新.当p=1时

  • pytorch 实现在测试的时候启用dropout

    pytorch 实现在测试的时候启用dropout

    我们知道,dropout一般都在训练的时候使用,那么测试的时候如何也开启dropout呢? 在pytorch中,网络有train和eval两种模式,在train模式下,dropout和batch normalization会生效,而val模式下,dropout不生效,bn固定参数. 想要在测试的时候使用dropout,可以把dropout单独设为train模式,这里可以使用apply函数: def apply_dropout(m): if type(m) == nn.Dropout: m.tra

  • Pytorch之如何dropout避免过拟合

    Pytorch之如何dropout避免过拟合

    一.做数据 二.搭建神经网络 三.训练 四.对比测试结果 注意:测试过程中,一定要注意模式切换 Pytorch的学习--过拟合 过拟合 过拟合是当数据量较小时或者输出结果过于依赖某些特定的神经元,训练神经网络训练会发生一种现象.出现这种现象的神经网络预测的结果并不具有普遍意义,其预测结果极不准确. 解决方法 1.增加数据量 2.L1,L2,L3-正规化,即在计算误差值的时候加上要学习的参数值,当参数改变过大时,误差也会变大,通过这种惩罚机制来控制过拟合现象 3.dropout正规化,在训练过程中

  • pytorch Dropout过拟合的操作

    pytorch Dropout过拟合的操作

    如下所示: import torch from torch.autograd import Variable import matplotlib.pyplot as plt torch.manual_seed(1) N_SAMPLES = 20 N_HIDDEN = 300 # training data x = torch.unsqueeze(torch.linspace(-1, 1, N_SAMPLES), 1) y = x + 0.3 * torch.normal(torch.zeros(

  • Python深度学习pytorch神经网络Dropout应用详解解

    Python深度学习pytorch神经网络Dropout应用详解解

    目录 扰动的鲁棒性 实践中的dropout 简洁实现 扰动的鲁棒性 在之前我们讨论权重衰减(L2​正则化)时看到的那样,参数的范数也代表了一种有用的简单性度量.简单性的另一个有用角度是平滑性,即函数不应该对其输入的微笑变化敏感.例如,当我们对图像进行分类时,我们预计向像素添加一些随机噪声应该是基本无影响的. dropout在正向传播过程中,计算每一内部层同时注入噪声,这已经成为训练神经网络的标准技术.这种方法之所以被称为dropout,因为我们从表面上看是在训练过程中丢弃(drop out)一些

  • Python深度学习pytorch神经网络图像卷积运算详解

    Python深度学习pytorch神经网络图像卷积运算详解

    目录 互相关运算 卷积层 特征映射 由于卷积神经网络的设计是用于探索图像数据,本节我们将以图像为例. 互相关运算 严格来说,卷积层是个错误的叫法,因为它所表达的运算其实是互相关运算(cross-correlation),而不是卷积运算.在卷积层中,输入张量和核张量通过互相关运算产生输出张量. 首先,我们暂时忽略通道(第三维)这一情况,看看如何处理二维图像数据和隐藏表示.下图中,输入是高度为3.宽度为3的二维张量(即形状为 3 × 3 3\times3 3×3).卷积核的高度和宽度都是2. 注意,

  • Python深度学习pytorch神经网络填充和步幅的理解

    Python深度学习pytorch神经网络填充和步幅的理解

    目录 填充 步幅 上图中,输入的高度和宽度都为3,卷积核的高度和宽度都为2,生成的输出表征的维度为 2 × 2 2\times2 2×2.从上图可看出卷积的输出形状取决于输入形状和卷积核的形状. 填充 以上面的图为例,在应用多层卷积时,我们常常丢失边缘像素. 解决这个问题的简单方法即为填充(padding):在输入图像的边界填充元素(通常填充元素是0). 例如,在上图中我们将 3 × 3 3\times3 3×3输入填充到 5 × 5 5\times5 5×5,那么它的输出就增加为 4 × 4

  • Python深度学习pytorch神经网络多输入多输出通道

    Python深度学习pytorch神经网络多输入多输出通道

    目录 多输入通道 多输出通道 1 × 1 1\times1 1×1卷积层 虽然每个图像具有多个通道和多层卷积层.例如彩色图像具有标准的RGB通道来指示红.绿和蓝.但是到目前为止,我们仅展示了单个输入和单个输出通道的简化例子.这使得我们可以将输入.卷积核和输出看作二维张量. 当我们添加通道时,我们的输入和隐藏的表示都变成了三维张量.例如,每个RGB输入图像具有 3 × h × w 3\times{h}\times{w} 3×h×w的形状.我们将这个大小为3的轴称为通道(channel)维度.在本节

  • Python深度学习pytorch神经网络汇聚层理解

    Python深度学习pytorch神经网络汇聚层理解

    目录 最大汇聚层和平均汇聚层 填充和步幅 多个通道 我们的机器学习任务通常会跟全局图像的问题有关(例如,"图像是否包含一只猫呢?"),所以我们最后一层的神经元应该对整个输入的全局敏感.通过逐渐聚合信息,生成越来越粗糙的映射,最终实现学习全局表示的目标,同时将卷积图层的所有有时保留在中间层. 此外,当检测较底层的特征时(例如之前讨论的边缘),我们通常希望这些特征保持某种程度上的平移不变性.例如,如果我们拍摄黑白之间轮廓清晰的图像X,并将整个图像向右移动一个像素,即Z[i, j] = X[

  • Python深度学习pytorch神经网络多层感知机简洁实现

    Python深度学习pytorch神经网络多层感知机简洁实现

    我们可以通过高级API更简洁地实现多层感知机. import torch from torch import nn from d2l import torch as d2l 模型 与softmax回归的简洁实现相比,唯一的区别是我们添加了2个全连接层.第一层是隐藏层,它包含256个隐藏单元,并使用了ReLU激活函数.第二层是输出层. net = nn.Sequential(nn.Flatten(), nn.Linear(784, 256), nn.ReLU(), nn.Linear(256, 1

  • Python深度学习pytorch神经网络块的网络之VGG

    Python深度学习pytorch神经网络块的网络之VGG

    目录 VGG块 VGG网络 训练模型 与芯片设计中工程师从放置晶体管到逻辑元件再到逻辑块的过程类似,神经网络结构的设计也逐渐变得更加抽象.研究人员开始从单个神经元的角度思考问题,发展到整个层次,现在又转向模块,重复各层的模式. 使用块的想法首先出现在牛津大学的视觉几何组(visualgeometry Group)(VGG)的VGG网络中.通过使用循环和子程序,可以很容易地在任何现代深度学习框架的代码中实现这些重复的结构. VGG块 经典卷积神经网络的基本组成部分是下面的这个序列: 1.带填充以保

  • Python深度学习pytorch卷积神经网络LeNet

    Python深度学习pytorch卷积神经网络LeNet

    目录 LeNet 模型训练 在本节中,我们将介绍LeNet,它是最早发布的卷积神经网络之一.这个模型是由AT&T贝尔实验室的研究院Yann LeCun在1989年提出的(并以其命名),目的是识别手写数字.当时,LeNet取得了与支持向量机性能相媲美的成果,成为监督学习的主流方法.LeNet被广泛用于自动取款机中,帮助识别处理支票的数字. LeNet 总体来看,LeNet(LeNet-5)由两个部分组成: 卷积编码器: 由两个卷积层组成 全连接层密集快: 由三个全连接层组成 每个卷积块中的基本单元

  • Python深度学习pyTorch权重衰减与L2范数正则化解析

    Python深度学习pyTorch权重衰减与L2范数正则化解析

    下面进行一个高维线性实验 假设我们的真实方程是: 假设feature数200,训练样本和测试样本各20个 模拟数据集 num_train,num_test = 10,10 num_features = 200 true_w = torch.ones((num_features,1),dtype=torch.float32) * 0.01 true_b = torch.tensor(0.5) samples = torch.normal(0,1,(num_train+num_test,num_fe

  • Python深度学习pytorch实现图像分类数据集

    Python深度学习pytorch实现图像分类数据集

    目录 读取数据集 读取小批量 整合所有组件 目前广泛使用的图像分类数据集之一是MNIST数据集.如今,MNIST数据集更像是一个健全的检查,而不是一个基准. 为了提高难度,我们将在接下来的章节中讨论在2017年发布的性质相似但相对复杂的Fashion-MNIST数据集. import torch import torchvision from torch.utils import data from torchvision import transforms from d2l import to

随机推荐