javascript中可能用得到的全部的排序算法

导读

排序算法可以称得上是我的盲点, 曾几何时当我知道Chrome的Array.prototype.sort使用了快速排序时, 我的内心是奔溃的(啥是快排, 我只知道冒泡啊?!), 要知道学习一门技术最好的时间是三年前, 但愿我现在补习还来得及(捂脸).

因此本篇重拾了出镜概率比较高的十来种排序算法, 逐一分析其排序思想, 并批注注意事项. 欢迎对算法提出改进和讨论.

冒泡排序

冒泡排序需要两个嵌套的循环. 其中, 外层循环移动游标; 内层循环遍历游标及之后(或之前)的元素, 通过两两交换的方式, 每次只确保该内循环结束位置排序正确, 然后内层循环周期结束, 交由外层循环往后(或前)移动游标, 随即开始下一轮内层循环, 以此类推, 直至循环结束.

Tips: 由于冒泡排序只在相邻元素大小不符合要求时才调换他们的位置, 它并不改变相同元素之间的相对顺序, 因此它是稳定的排序算法.

由于有两层循环, 因此可以有四种实现方式.

方案	外层循环	内层循环
1	正序	正序
2	正序	逆序
3	逆序	正序
4	逆序	逆序

四种不同循环方向, 实现方式略有差异.

如下是动图效果(对应于方案1: 内/外层循环均是正序遍历.

如下是上图的算法实现(对应方案一: 内/外层循环均是正序遍历).

//先将交换元素部分抽象出来
function swap(i,j,array){
 var temp = array[j];
 array[j] = array[i];
 array[i] = temp;
}

function bubbleSort(array) {
 var length = array.length, isSwap;
 for (var i = 0; i < length; i++) { //正序
 isSwap = false;
 for (var j = 0; j < length - 1 - i; j++) { //正序
 array[j] > array[j+1] && (isSwap = true) && swap(j,j+1,array);
 }
 if(!isSwap)
 break;
 }
 return array;
}

以上, 排序的特点就是: 靠后的元素位置先确定.

方案二: 外循环正序遍历, 内循环逆序遍历, 代码如下:

function bubbleSort(array) {
 var length = array.length, isSwap;
 for (var i = 0; i < length; i++) { //正序
 isSwap = false;
 for (var j = length - 1; j >= i+1; j--) { //逆序
 array[j] < array[j-1] && (isSwap = true) && swap(j,j-1,array);
 }
 if(!isSwap)
 break;
 }
 return array;
}

以上, 靠前的元素位置先确定.

方案三: 外循环逆序遍历, 内循环正序遍历, 代码如下:

function bubbleSort(array) {
 var length = array.length, isSwap;
 for (var i = length - 1; i >= 0; i--) { //逆序
 isSwap = false;
 for (var j = 0; j < i; j++) { //正序
 array[j] > array[j+1] && (isSwap = true) && swap(j,j+1,array);
 }
 if(!isSwap)
 break;
 }
 return array;
}

以上, 由于内循环是正序遍历, 因此靠后的元素位置先确定.

方案四: 外循环逆序遍历, 内循环逆序遍历, 代码如下:

function bubbleSort(array) {
 var length = array.length, isSwap;
 for (var i = length - 1; i >= 0; i--) { //逆序
 isSwap = false;
 for (var j = length - 1; j >= length - 1 - i; j--) { //逆序
 array[j] < array[j-1] && (isSwap = true) && swap(j,j-1,array);
 }
 if(!isSwap)
 break;
 }
 return array;
}

以上, 由于内循环是逆序遍历, 因此靠前的元素位置先确定.

以下是其算法复杂度:

平均时间复杂度	最好情况	最坏情况	空间复杂度
O(n²)	O(n)	O(n²)	O(1)

冒泡排序是最容易实现的排序, 最坏的情况是每次都需要交换, 共需遍历并交换将近n²/2次, 时间复杂度为O(n²). 最佳的情况是内循环遍历一次后发现排序是对的, 因此退出循环, 时间复杂度为O(n). 平均来讲, 时间复杂度为O(n²). 由于冒泡排序中只有缓存的temp变量需要内存空间, 因此空间复杂度为常量O(1).

双向冒泡排序

双向冒泡排序是冒泡排序的一个简易升级版, 又称鸡尾酒排序. 冒泡排序是从低到高(或者从高到低)单向排序, 双向冒泡排序顾名思义就是从两个方向分别排序(通常, 先从低到高, 然后从高到低). 因此它比冒泡排序性能稍好一些.

如下是算法实现:

function bothwayBubbleSort(array){
 var tail = array.length-1, i, isSwap = false;
 for(i = 0; i < tail; tail--){
 for(var j = tail; j > i; j--){ //第一轮, 先将最小的数据冒泡到前面
 array[j-1] > array[j] && (isSwap = true) && swap(j,j-1,array);
 }
 i++;
 for(j = i; j < tail; j++){ //第二轮, 将最大的数据冒泡到后面
 array[j] > array[j+1] && (isSwap = true) && swap(j,j+1,array);
 }
 }
 return array;
}

选择排序

从算法逻辑上看, 选择排序是一种简单且直观的排序算法. 它也是两层循环. 内层循环就像工人一样, 它是真正做事情的, 内层循环每执行一遍, 将选出本次待排序的元素中最小(或最大)的一个, 存放在数组的起始位置. 而 外层循环则像老板一样, 它告诉内层循环你需要不停的工作, 直到工作完成(也就是全部的元素排序完成).

Tips: 选择排序每次交换的元素都有可能不是相邻的, 因此它有可能打破原来值为相同的元素之间的顺序. 比如数组[2,2,1,3], 正向排序时, 第一个数字2将与数字1交换, 那么两个数字2之间的顺序将和原来的顺序不一致, 虽然它们的值相同, 但它们相对的顺序却发生了变化. 我们将这种现象称作 不稳定性 .

如下是动图效果:

如下是上图的算法实现:

function selectSort(array) {
 var length = array.length, min;
 for (var i = 0; i < length - 1; i++) {
 min = i;
 for (var j = i + 1; j < length; j++) {
 array[j] < array[min] && (min = j); //记住最小数的下标
 }
 min!=i && swap(i,min,array);
 }
 return array;
}

以下是其算法复杂度:

平均时间复杂度	最好情况	最坏情况	空间复杂度
O(n²)	O(n²)	O(n²)	O(1)

选择排序的简单和直观名副其实, 这也造就了它”出了名的慢性子”, 无论是哪种情况, 哪怕原数组已排序完成, 它也将花费将近n²/2次遍历来确认一遍. 即便是这样, 它的排序结果也还是不稳定的. 唯一值得高兴的是, 它并不耗费额外的内存空间.

插入排序

插入排序的设计初衷是往有序的数组中快速插入一个新的元素. 它的算法思想是: 把要排序的数组分为了两个部分, 一部分是数组的全部元素(除去待插入的元素), 另一部分是待插入的元素; 先将第一部分排序完成, 然后再插入这个元素. 其中第一部分的排序也是通过再次拆分为两部分来进行的.

插入排序由于操作不尽相同, 可分为 直接插入排序 , 折半插入排序(又称二分插入排序), 链表插入排序 , 希尔排序 .

直接插入排序

它的基本思想是: 将待排序的元素按照大小顺序, 依次插入到一个已经排好序的数组之中, 直到所有的元素都插入进去.

如下是动图效果:

如下是上图的算法实现:

function directInsertionSort(array) {
 var length = array.length, index, current;
 for (var i = 1; i < length; i++) {
 index = i - 1; //待比较元素的下标
 current = array[i]; //当前元素
 while(index >= 0 && array[index] > current) { //前置条件之一:待比较元素比当前元素大
 array[index+1] = array[index]; //将待比较元素后移一位
 index--;  //游标前移一位
 //console.log(array);
 }
 if(index+1 != i){  //避免同一个元素赋值给自身
 array[index+1] = current; //将当前元素插入预留空位
 //console.log(array);
 }
 }
 return array;
}

为了更好的观察到直接插入排序的实现过程, 我们不妨将上述代码中的注释部分加入. 以数组 [5,4,3,2,1] 为例, 如下便是原数组的演化过程.

可见, 数组的各个元素, 从后往前, 只要比前面的元素小, 都依次插入到了合理的位置.

Tips: 由于直接插入排序每次只移动一个元素的位置, 并不会改变值相同的元素之间的排序, 因此它是一种稳定排序.

折半插入排序

折半插入排序是直接插入排序的升级版. 鉴于插入排序第一部分为已排好序的数组, 我们不必按顺序依次寻找插入点, 只需比较它们的中间值与待插入元素的大小即可.

Tips: 同直接插入排序类似, 折半插入排序每次交换的是相邻的且值为不同的元素, 它并不会改变值相同的元素之间的顺序. 因此它是稳定的.

算法基本思想是:

1. 取0 ~ i-1的中间点( m = (i-1)>>1 ), array[i] 与 array[m] 进行比较, 若array[i] < array[m] , 则说明待插入的元素array[i] 应该处于数组的 0 ~ m 索引之间; 反之, 则说明它应该处于数组的 m ~ i-1 索引之间.
2. 重复步骤1, 每次缩小一半的查找范围, 直至找到插入的位置.
3. 将数组中插入位置之后的元素全部后移一位.
4. 在指定位置插入第 i 个元素.

注: x>>1 是位运算中的右移运算, 表示右移一位, 等同于x除以2再取整, 即 x>>1 == Math.floor(x/2) .

如下是算法实现:

function binaryInsertionSort(array){
 var current, i, j, low, high, m;
 for(i = 1; i < array.length; i++){
 low = 0;
 high = i - 1;
 current = array[i];

 while(low <= high){ //步骤1&2:折半查找
 m = (low + high)>>1;
 if(array[i] >= array[m]){//值相同时, 切换到高半区，保证稳定性
 low = m + 1; //插入点在高半区
 }else{
 high = m - 1; //插入点在低半区
 }
 }
 for(j = i; j > low; j--){ //步骤3:插入位置之后的元素全部后移一位
 array[j] = array[j-1];
 }
 array[low] = current; //步骤4:插入该元素
 }
 return array;
}

为了便于对比, 同样以数组 [5,4,3,2,1] 举例🌰. 原数组的演化过程如下(与上述一样):

虽然折半插入排序明显减少了查询的次数, 但是数组元素移动的次数却没有改变. 它们的时间复杂度都是O(n²).

希尔排序

希尔排序也称缩小增量排序, 它是直接插入排序的另外一个升级版, 实质就是分组插入排序. 希尔排序以其设计者希尔(Donald Shell)的名字命名, 并于1959年公布.

算法的基本思想:

1. 将数组拆分为若干个子分组, 每个分组由相距一定”增量”的元素组成. 比方说将[0,1,2,3,4,5,6,7,8,9,10]的数组拆分为”增量”为5的分组, 那么子分组分别为 [0,5], [1,6], [2,7], [3,8], [4,9] 和 [5,10].
2. 然后对每个子分组应用直接插入排序.
3. 逐步减小”增量”, 重复步骤1,2.
4. 直至”增量”为1, 这是最后一个排序, 此时的排序, 也就是对全数组进行直接插入排序.

如下是排序的示意图:

可见, 希尔排序实际上就是不断的进行直接插入排序, 分组是为了先将局部元素有序化. 因为直接插入排序在元素基本有序的状态下, 效率非常高. 而希尔排序呢, 通过先分组后排序的方式, 制造了直接插入排序高效运行的场景. 因此希尔排序效率更高.

我们试着抽象出共同点, 便不难发现上述希尔排序的第四步就是一次直接插入排序, 而希尔排序原本就是从”增量”为n开始, 直至”增量”为1, 循环应用直接插入排序的一种封装. 因此直接插入排序就可以看做是步长为1的希尔排序. 为此我们先来封装下直接插入排序.

//形参增加步数gap(实际上就相当于gap替换了原来的数字1)
function directInsertionSort(array, gap) {
 gap = (gap == undefined) ? 1 : gap; //默认从下标为1的元素开始遍历
 var length = array.length, index, current;
 for (var i = gap; i < length; i++) {
 index = i - gap; //待比较元素的下标
 current = array[i]; //当前元素
 while(index >= 0 && array[index] > current) { //前置条件之一:待比较元素比当前元素大
 array[index + gap] = array[index]; //将待比较元素后移gap位
 index -= gap;  //游标前移gap位
 }
 if(index + gap != i){  //避免同一个元素赋值给自身
 array[index + gap] = current; //将当前元素插入预留空位
 }
 }
 return array;
}

那么希尔排序的算法实现如下:

function shellSort(array){
 var length = array.length, gap = length>>1, current, i, j;
 while(gap > 0){
 directInsertionSort(array, gap); //按指定步长进行直接插入排序
 gap = gap>>1;
 }
 return array;
}

同样以数组[5,4,3,2,1] 举例🌰. 原数组的演化过程如下:

对比上述直接插入排序和折半插入排序, 数组元素的移动次数由14次减少为7次. 通过拆分原数组为粒度更小的子数组, 希尔排序进一步提高了排序的效率.

不仅如此, 以上步长设置为了 {N/2, (N/2)/2, …, 1}. 该序列即希尔增量, 其它的增量序列 还有Hibbard：{1, 3, …, 2^k-1}. 通过合理调节步长, 还能进一步提升排序效率. 实际上已知的最好步长序列是由Sedgewick提出的(1, 5, 19, 41, 109,…). 该序列中的项或者是9*4^i - 9*2^i + 1或者是4^i - 3*2^i + 1. 具体请戳 希尔排序-维基百科 .

Tips: 我们知道, 单次直接插入排序是稳定的, 它不会改变相同元素之间的相对顺序, 但在多次不同的插入排序过程中, 相同的元素可能在各自的插入排序中移动, 可能导致相同元素相对顺序发生变化. 因此, 希尔排序并不稳定.

归并排序

归并排序建立在归并操作之上, 它采取分而治之的思想, 将数组拆分为两个子数组, 分别排序, 最后才将两个子数组合并; 拆分的两个子数组, 再继续递归拆分为更小的子数组, 进而分别排序, 直到数组长度为1, 直接返回该数组为止.

Tips: 归并排序严格按照从左往右(或从右往左)的顺序去合并子数组, 它并不会改变相同元素之间的相对顺序, 因此它也是一种稳定的排序算法.

如下是动图效果:

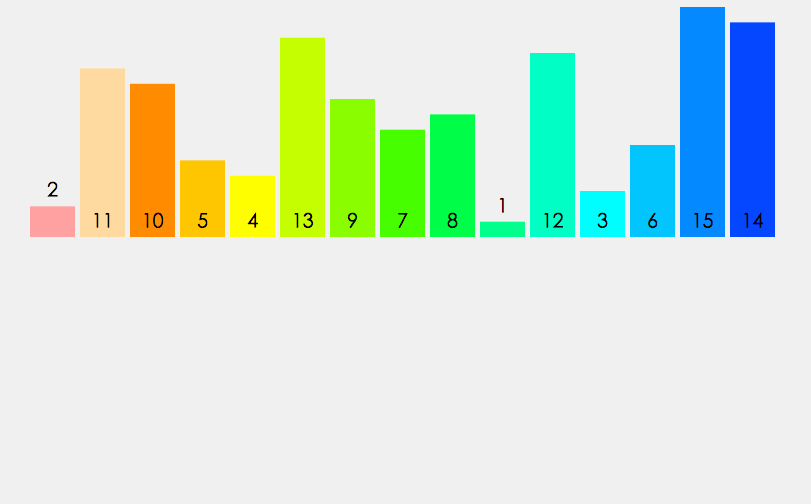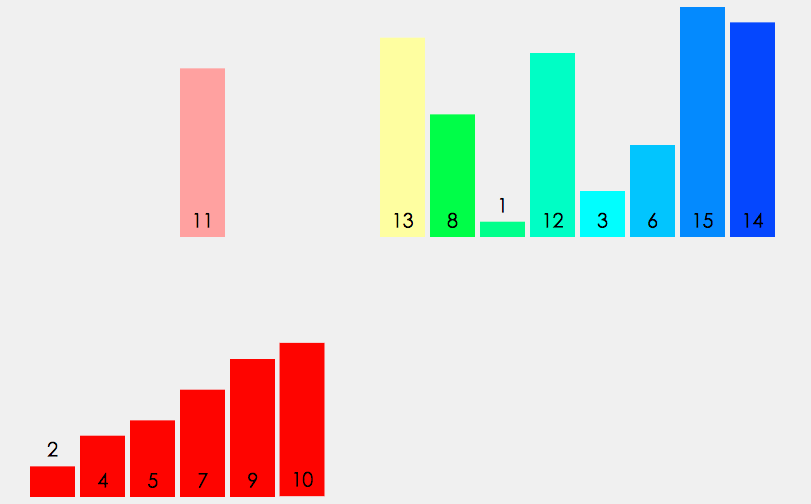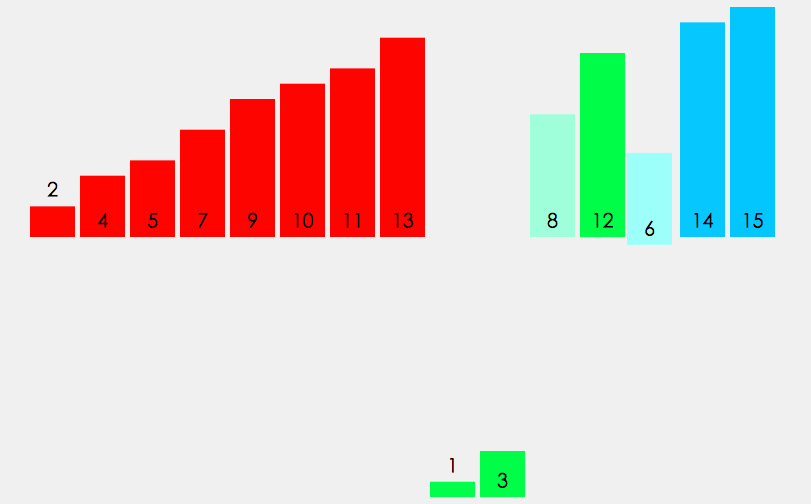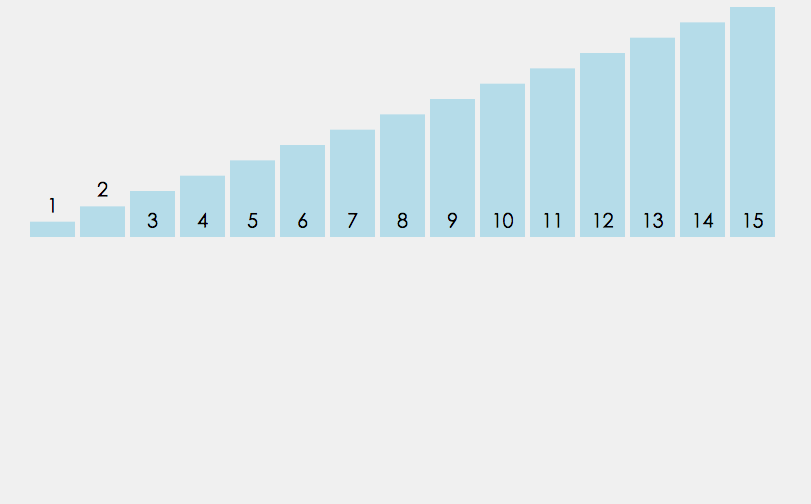
归并排序可通过两种方式实现:

1. 自上而下的递归
2. 自下而上的迭代

如下是算法实现(方式1:递归):

function mergeSort(array) { //采用自上而下的递归方法
 var length = array.length;
 if(length < 2) {
 return array;
 }
 var m = (length >> 1),
 left = array.slice(0, m),
 right = array.slice(m); //拆分为两个子数组
 return merge(mergeSort(left), mergeSort(right));//子数组继续递归拆分,然后再合并
}
function merge(left, right){ //合并两个子数组
 var result = [];
 while (left.length && right.length) {
 var item = left[0] <= right[0] ? left.shift() : right.shift();//注意:判断的条件是小于或等于,如果只是小于,那么排序将不稳定.
 result.push(item);
 }
 return result.concat(left.length ? left : right);
}

由上, 长度为n的数组, 最终会调用mergeSort函数2n-1次. 通过自上而下的递归实现的归并排序, 将存在堆栈溢出的风险. 亲测各浏览器的堆栈溢出所需的递归调用次数大致为:

Chrome v55: 15670
Firefox v50: 44488
Safari v9.1.2: 50755

以下是测试代码:

function computeMaxCallStackSize() {
 try {
 return 1 + computeMaxCallStackSize();
 } catch (e) {
 // Call stack overflow
 return 1;
 }
}
var time = computeMaxCallStackSize();
console.log(time);

为此, ES6规范中提出了尾调优化的思想: 如果一个函数的最后一步也是一个函数调用, 那么该函数所需要的栈空间将被释放, 它将直接进入到下次调用中, 最终调用栈里只保留最后一次的调用记录.

虽然ES6规范如此诱人, 然而目前并没有浏览器支持尾调优化, 相信在不久的将来, 尾调优化就会得到主流浏览器的支持.

以下是其算法复杂度:

平均时间复杂度	最好情况	最坏情况	空间复杂度
O(nlog₂n)	O(nlog₂n)	O(nlog₂n)	O(n)

从效率上看, 归并排序可算是排序算法中的”佼佼者”. 假设数组长度为n, 那么拆分数组共需logn步, 又每步都是一个普通的合并子数组的过程, 时间复杂度为O(n), 故其综合时间复杂度为O(nlogn). 另一方面, 归并排序多次递归过程中拆分的子数组需要保存在内存空间, 其空间复杂度为O(n).

快速排序

快速排序借用了分治的思想, 并且基于冒泡排序做了改进. 它由C. A. R. Hoare在1962年提出. 它将数组拆分为两个子数组, 其中一个子数组的所有元素都比另一个子数组的元素小, 然后对这两个子数组再重复进行上述操作, 直到数组不可拆分, 排序完成.

如下是动图效果:

如下是算法实现:

function quickSort(array, left, right) {
 var partitionIndex,
 left = typeof left == 'number' ? left : 0,
 right = typeof right == 'number' ? right : array.length-1;
 if (left < right) {
 partitionIndex = partition(array, left, right);//切分的基准值
 quickSort(array, left, partitionIndex-1);
 quickSort(array, partitionIndex+1, right);
 }
 return array;
}
function partition(array, left ,right) { //分区操作
 for (var i = left+1, j = left; i <= right; i++) {//j是较小值存储位置的游标
 array[i] < array[left] && swap(i, ++j, array);//以第一个元素为基准
 }
 swap(left, j, array); //将第一个元素移至中间
 return j;
}

以下是其算法复杂度:

平均时间复杂度	最好情况	最坏情况	空间复杂度
O(nlog₂n)	O(nlog₂n)	O(n²)	O(nlog₂n)

快速排序排序效率非常高. 虽然它运行最糟糕时将达到O(n²)的时间复杂度, 但通常, 平均来看, 它的时间复杂为O(nlogn), 比同样为O(nlogn)时间复杂度的归并排序还要快. 快速排序似乎更偏爱乱序的数列, 越是乱序的数列, 它相比其他排序而言, 相对效率更高. 之前在 捋一捋JS的数组 一文中就提到: Chrome的v8引擎为了高效排序, 在排序数据超过了10条时, 便会采用快速排序. 对于10条及以下的数据采用的便是插入排序.

Tips: 同选择排序相似, 快速排序每次交换的元素都有可能不是相邻的, 因此它有可能打破原来值为相同的元素之间的顺序. 因此, 快速排序并不稳定.

堆排序

1991年的计算机先驱奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德(Robert W．Floyd) 和威廉姆斯(J．Williams) 在1964年共同发明了著名的堆排序算法(Heap Sort).

堆排序是利用堆这种数据结构所设计的一种排序算法. 它是选择排序的一种. 堆分为大根堆和小根堆. 大根堆要求每个子节点的值都不大于其父节点的值, 即array[childIndex] <= array[parentIndex], 最大的值一定在堆顶. 小根堆与之相反, 即每个子节点的值都不小于其父节点的值, 最小的值一定在堆顶. 因此我们可使用大根堆进行升序排序, 使用小根堆进行降序排序.

并非所有的序列都是堆, 对于序列k1, k2,…kn, 需要满足如下条件才行:

ki <= k(2i) 且 ki<=k(2i+1)(1≤i≤ n/2), 即为小根堆, 将<=换成>=, 那么则是大根堆. 我们可以将这里的堆看作完全二叉树, k(i) 相当于是二叉树的非叶子节点, k(2i) 则是左子节点, k(2i+1)是右子节点.

算法的基本思想(以大根堆为例):

1. 先将初始序列K[1..n]建成一个大根堆, 此堆为初始的无序区.
2. 再将关键字最大的记录K1 (即堆顶)和无序区的最后一个记录K[n]交换, 由此得到新的无序区K[1..n-1]和有序区K[n], 且满足K[1..n-1].keys≤K[n].key
3. 交换K1 和 K[n] 后, 堆顶可能违反堆性质, 因此需将K[1..n-1]调整为堆. 然后重复步骤2, 直到无序区只有一个元素时停止.

如下是动图效果:

如下是算法实现:

function heapAdjust(array, i, length) {//堆调整
 var left = 2 * i + 1,
 right = 2 * i + 2,
 largest = i;
 if (left < length && array[largest] < array[left]) {
 largest = left;
 }
 if (right < length && array[largest] < array[right]) {
 largest = right;
 }
 if (largest != i) {
 swap(i, largest, array);
 heapAdjust(array, largest, length);
 }
}
function heapSort(array) {
 //建立大顶堆
 length = array.length;
 for (var i = length>>1; i >= 0; i--) {
 heapAdjust(array, i, length);
 }
 //调换第一个与最后一个元素,重新调整为大顶堆
 for (var i = length - 1; i > 0; i--) {
 swap(0, i, array);
 heapAdjust(array, 0, --length);
 }
 return array;
}

以上, ①建立堆的过程, 从length/2 一直处理到0, 时间复杂度为O(n);

②调整堆的过程是沿着堆的父子节点进行调整, 执行次数为堆的深度, 时间复杂度为O(lgn);

③堆排序的过程由n次第②步完成, 时间复杂度为O(nlgn).

Tips: 由于堆排序中初始化堆的过程比较次数较多, 因此它不太适用于小序列. 同时由于多次任意下标相互交换位置, 相同元素之间原本相对的顺序被破坏了, 因此, 它是不稳定的排序.

计数排序

计数排序几乎是唯一一个不基于比较的排序算法, 该算法于1954年由 Harold H. Seward 提出. 使用它处理一定范围内的整数排序时, 时间复杂度为O(n+k), 其中k是整数的范围, 它几乎比任何基于比较的排序算法都要快( 只有当O(k)>O(n*log(n))的时候其效率反而不如基于比较的排序, 如归并排序和堆排序).

使用计数排序需要满足如下条件:

• 待排序的序列全部为整数
• 排序需要额外的存储空间

算法的基本思想:

计数排序利用了一个特性, 对于数组的某个元素, 一旦知道了有多少个其它元素比它小(假设为m个), 那么就可以确定出该元素的正确位置(第m+1位)

1. 获取待排序数组A的最大值, 最小值.
2. 将最大值与最小值的差值+1作为长度新建计数数组B，并将相同元素的数量作为值存入计数数组.
3. 对计数数组B累加计数, 存储不同值的初始下标.
4. 从原数组A挨个取值, 赋值给一个新的数组C相应的下标, 最终返回数组C.

注意: 如果原数组A是包含若干个对象的数组，需要基于对象的某个属性进行排序，那么算法开始时，需要将原数组A处理为一个只包含对象属性值的简单数组simpleA, 接下来便基于simpleA进行计数、累加计数, 其它同上.

如下是动图效果:

如下是算法实现:

function countSort(array, keyName){
 var length = array.length,
 output = new Array(length),
 max,
 min,
 simpleArray = keyName ? array.map(function(v){
 return v[keyName];
 }) : array; // 如果keyName是存在的，那么就创建一个只有keyValue的简单数组

 // 获取最大最小值
 max = min = simpleArray[0];
 simpleArray.forEach(function(v){
 v > max && (max = v);
 v < min && (min = v);
 });
 // 获取计数数组的长度
 var k = max - min + 1;
 // 新建并初始化计数数组
 var countArray = new Array(k);
 simpleArray.forEach(function(v){
 countArray[v - min]= (countArray[v - min] || 0) + 1;
 });
 // 累加计数，存储不同值的初始下标
 countArray.reduce(function(prev, current, i, arr){
 arr[i] = prev;
 return prev + current;
 }, 0);
 // 从原数组挨个取值(因取的是原数组的相应值，只能通过遍历原数组来实现)
 simpleArray.forEach(function(v, i){
 var j = countArray[v - min]++;
 output[j] = array[i];
 });
 return output;
}

以上实现不仅支持了数值序列的排序，还支持根据对象的某个属性值来排序。测试如下：

var a = [2, 1, 1, 3, 2, 1, 4, 2],
 b = [
 {id: 2, s:'a'},
 {id: 1, s: 'b'},
 {id: 1, s: 'c'},
 {id: 3, s: 'd'},
 {id: 2, s: 'e'},
 {id: 1, s: 'f'},
 {id: 4, s: 'g'},
 {id: 2, s: 'h'}
 ];
countSort(a); // [1, 1, 1, 2, 2, 2, 3, 4]
countSort(b, 'id'); // [{id:1,s:'b'},{id:1,s:'c'},{id:1,s:'f'},{id:2,s:'a'},{id:2,s:'e'},{id:2,s:'h'},{id:3,s:'d'},{id:4,s:'g'}]

Tips: 计数排序不改变相同元素之间原本相对的顺序, 因此它是稳定的排序算法.

桶排序

桶排序即所谓的箱排序, 它是将数组分配到有限数量的桶子里. 每个桶里再各自排序(因此有可能使用别的排序算法或以递归方式继续桶排序). 当每个桶里的元素个数趋于一致时, 桶排序只需花费O(n)的时间. 桶排序通过空间换时间的方式提高了效率, 因此它需要额外的存储空间(即桶的空间).

算法的基本思想:

桶排序的核心就在于怎么把元素平均分配到每个桶里, 合理的分配将大大提高排序的效率.

如下是算法实现:

function bucketSort(array, bucketSize) {
 if (array.length === 0) {
 return array;
 }

 var i = 1,
 min = array[0],
 max = min;
 while (i++ < array.length) {
 if (array[i] < min) {
 min = array[i]; //输入数据的最小值
 } else if (array[i] > max) {
 max = array[i]; //输入数据的最大值
 }
 }

 //桶的初始化
 bucketSize = bucketSize || 5; //设置桶的默认大小为5
 var bucketCount = ~~((max - min) / bucketSize) + 1, //桶的个数
 buckets = new Array(bucketCount); //创建桶
 for (i = 0; i < buckets.length; i++) {
 buckets[i] = []; //初始化桶
 }

 //将数据分配到各个桶中,这里直接按照数据值的分布来分配,一定范围内均匀分布的数据效率最为高效
 for (i = 0; i < array.length; i++) {
 buckets[~~((array[i] - min) / bucketSize)].push(array[i]);
 }

 array.length = 0;
 for (i = 0; i < buckets.length; i++) {
 quickSort(buckets[i]); //对每个桶进行排序，这里使用了快速排序
 for (var j = 0; j < buckets[i].length; j++) {
 array.push(buckets[i][j]); //将已排序的数据写回数组中
 }
 }
 return array;
}

Tips: 桶排序本身是稳定的排序, 因此它的稳定性与桶内排序的稳定性保持一致.

实际上, 桶也只是一个抽象的概念, 它的思想与归并排序,快速排序等类似, 都是通过将大量数据分配到N个不同的容器中, 分别排序, 最后再合并数据. 这种方式大大减少了排序时整体的遍历次数, 提高了算法效率.

基数排序

基数排序源于老式穿孔机, 排序器每次只能看到一个列. 它是基于元素值的每个位上的字符来排序的. 对于数字而言就是分别基于个位, 十位, 百位 或千位等等数字来排序. (不明白不要紧, 我也不懂, 请接着往下读)

按照优先从高位或低位来排序有两种实现方案:

• MSD: 由高位为基底, 先按k1排序分组, 同一组中记录, 关键码k1相等, 再对各组按k2排序分成子组, 之后, 对后面的关键码继续这样的排序分组, 直到按最次位关键码kd对各子组排序后. 再将各组连接起来, 便得到一个有序序列. MSD方式适用于位数多的序列.
• LSD: 由低位为基底, 先从kd开始排序，再对kd-1进行排序，依次重复，直到对k1排序后便得到一个有序序列. LSD方式适用于位数少的序列.

如下是LSD的动图效果:

如下是算法实现:

function radixSort(array, max) {
 var buckets = [],
 unit = 10,
 base = 1;
 for (var i = 0; i < max; i++, base *= 10, unit *= 10) {
 for(var j = 0; j < array.length; j++) {
 var index = ~~((array[j] % unit) / base);//依次过滤出个位,十位等等数字
 if(buckets[index] == null) {
 buckets[index] = []; //初始化桶
 }
 buckets[index].push(array[j]);//往不同桶里添加数据
 }
 var pos = 0,
 value;
 for(var j = 0, length = buckets.length; j < length; j++) {
 if(buckets[j] != null) {
 while ((value = buckets[j].shift()) != null) {
  array[pos++] = value; //将不同桶里数据挨个捞出来,为下一轮高位排序做准备,由于靠近桶底的元素排名靠前,因此从桶底先捞
 }
 }
 }
 }
 return array;
}

以上算法, 如果用来比较时间, 先按日排序, 再按月排序, 最后按年排序, 仅需排序三次.

基数排序更适合用于对时间, 字符串等这些整体权值未知的数据进行排序.

Tips: 基数排序不改变相同元素之间的相对顺序, 因此它是稳定的排序算法.

小结

各种排序性能对比如下:

排序类型	平均情况	最好情况	最坏情况	辅助空间	稳定性
冒泡排序	O(n²)	O(n)	O(n²)	O(1)	稳定
选择排序	O(n²)	O(n²)	O(n²)	O(1)	不稳定
直接插入排序	O(n²)	O(n)	O(n²)	O(1)	稳定
折半插入排序	O(n²)	O(n)	O(n²)	O(1)	稳定
希尔排序	O(n^1.3)	O(nlogn)	O(n²)	O(1)	不稳定
归并排序	O(nlog₂n)	O(nlog₂n)	O(nlog₂n)	O(n)	稳定
快速排序	O(nlog₂n)	O(nlog₂n)	O(n²)	O(nlog₂n)	不稳定
堆排序	O(nlog₂n)	O(nlog₂n)	O(nlog₂n)	O(1)	不稳定
计数排序	O(n+k)	O(n+k)	O(n+k)	O(k)	稳定
桶排序	O(n+k)	O(n+k)	O(n²)	O(n+k)	(不)稳定
基数排序	O(d(n+k))	O(d(n+k))	O(d(n+kd))	O(n+kd)	稳定

注: 桶排序的稳定性取决于桶内排序的稳定性, 因此其稳定性不确定. 基数排序中, k代表关键字的基数, d代表长度, n代表关键字的个数.

愿以此文怀念下我那远去的算法课程.

未完待续…

感谢 http://visualgo.net/ 提供图片支持. 特别感谢 不是小羊的肖恩 在简书上发布的 JS家的排序算法 提供的讲解.