例题详解Java dfs与记忆化搜索和分治递归算法的使用

目录

• 一、dfs（深度优先搜索）
• 1.图的dfs
• 2.树的dfs
• 二、记忆化搜索
• 1.普通递归：O(2^n)
• 2.记忆化搜索: O(n)
• 三、分治
• 四、算法题
• 1.dia和威严
• 示例
• 2.小红点点点
• 示例1
• 3.kotori和素因子
• 示例1
• 示例2
• 4.kotori和糖果
• 示例

一、dfs（深度优先搜索）

1.图的dfs

/**
 * 深度优先搜索
 *
 * @param node
 * @param set
 */
public void DFS(Node node, Set<Node> set) {
    if (node == null) {
        //当没有节点时，退出此次方法
        return;
    }
    if (!set.contains(node)) {
        //没有搜到过就保存，并且继续向下推进
        set.add(node);
        System.out.print(node.value + " ");
        for (Node node1 : node.nexts) {
            DFS(node1, set);
        }
    }
}

2.树的dfs

树（边数=顶点数-1的图）的dfs

public static void dfs(Node treeNode) {
        if (treeNode == null) {
            return;
        }
        System.out.print(treeNode.value + " ");
        // 遍历左节点
        dfs(treeNode.left);
        // 遍历右节点
        dfs(treeNode.right);
    }

使用dfs代替状压枚举：  dfs 优于 状压枚举

二、记忆化搜索

记忆化搜索，指通过记录已经搜索到的值来降低重复操作次数，从而加快运行速度。

斐波那契数列问题： 1,1,2,3,5,8,... 求斐波那契数列第n项

1.普通递归：O(2^n)

public static int f(int n){
    if(n<=1)return 1;
    return f(n-1)+f(n-2);
}

2.记忆化搜索: O(n)

    static int[] dp = new int[1000] ;
    public static int f1(int n){
        if(n<=1) return dp[n] = 1;
        if(dp[n]!=0)return dp[n];
        return dp[n]=f1(n-1)+f1(n-2);
    }

三、分治

将问题拆分成子问题进行求解。

例如归并排序： 1,4,7,2,5,8,3,6,9

第一步 拆分： 左边：1,4,7,2 右边：5,8,3,6,9

第二步 递归排序 左边：1,2,4,7 右边：3,5,6,8,9

第三步 合并两个有序数组 左边：1,2,4,7 右边：3,5,6,8,9

四、算法题

1.dia和威严

难度

知识点：dfs

从根开始dfs即可，dfs的过程中就能找到每个点需要的时间，维护一下最大值。

题目描述：

dia是学生会长。她经常有信息要传达给别人。

学生会的阶层等级森严。每个阶级传达信息只能传达到自己的下属。

一个人可以有多个下属，但一个人最多只能有一个上级。（树）

dia作为学生会长，很明显是没有上级的（即全学生会权利最大者）。

已知每个人传达到下属所消耗的时间。（传达给不同的下属，时间不一定相同） 现在dia有一个信息要传达给一个指定者。只有信息接收的指定者才需要理解信息（花费ai的时间）。她不想让效率太慢，于是她想找出最大时间消耗的那个路线（包括信息接收指定者所需要理解信息的时间），这样就能方便整改。

输入描述:

第一行一个正整数n，代表学生会的人数（dia是1号，其他人标记为2号到n号）。 （1≤n≤200000）第二行有n-1个正整数ai，代表从2号到n号，每个人需要理解信息的时间。 （1≤a1≤100）接下来的n-1行，每行有3个正整数x,y,k,代表x是y的上级，x向y传播信息需要消耗k的时间。（1≤x,y≤n,1≤k≤100）

输出描述:

一个正整数，代表dia选定某人作为信息接收指定者后，花费总时间的最大值。

示例

输入

3

3 4

1 2 4

1 3 2

输出

7

说明

若dia指定3号为信息接受者，消耗时间为2+4=6。

若dia指定2号为信息接受者，消耗为4+3=7。

故最大值为7。

备注:

注：只有指定者需要理解信息，传达者不需要花费时间理解信息。

import java.util.*;
import java.io.*;
public class Main{
    static class Edge{
        int to;
        int weight;
        //保存子节点，与线权（传播时间）。
        Edge(int to,int weight){
            this.to = to;
            this.weight = weight;
        }
    }
    static ArrayList<Edge>[] g;
    static int maxtime;
    static int weight[];
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine()); //n为总人数
        weight = new int[n+1];
        g = new ArrayList[n+1];
        // 每个桶中保存一个ArrayList（可达）
        //这里的i代表了第几个数（从1开始）
        for(int i = 1;i<=n;i++){
            g[i] = new ArrayList();
        }
        //保存所有点权（理解时间）纪录了从2到n的点权，与数字的位子相对应。
        String[] s = br.readLine().split(" ");
        for(int i = 0;i<n-1;i++){
            weight[i+2] = Integer.parseInt(s[i]);
        }
        for(int i = 0;i<n-1;i++){
            String[] s1 = br.readLine().split(" ");
            int x = Integer.parseInt(s1[0]);
            int y = Integer.parseInt(s1[1]);
            int z = Integer.parseInt(s1[2]);
            g[x].add(new Edge(y,z));
        }
        dfs(1,0);
        System.out.println(maxtime);
    }
    static void dfs(int i ,int time){
        if(maxtime<time+weight[i])maxtime = time+weight[i];
        for(int k = 0;k<g[i].size();k++){
            dfs(g[i].get(k).to,time+g[i].get(k).weight);
        }
    }
}

非常典型的dfs模板题目：dfs一个树，寻找根到某点的线权总合+某点的点权

思考：？？？

思考1：假如变成根到某点的线权总合+根到某点的点权总合，程序应该怎么改？

解：

dfs(g[i].get(k).to,time+g[i].get(k).weight+weight[i]);//那就加个点权

思考2：假如变成根到叶子点的线权总合+叶子点的点权，程序应该怎么改？

(1)首先思考一个问题：这个递归没有任何判断结束的条件。他是怎么结束的？

因为我们将他递归的过程安排的明明白白，他只是在执行有序有限的递归操作。所以没有给出判断条件。

(2)那么我们应该怎么判断他到叶子节点了呢？

我们单单在递归的代码上修改是不能判断出是否到达了叶子节点，所以还需要想清楚结构体是咋样的。

解：

if(maxtime<time+weight[i]&&g[i].isEmpty())maxtime = time+weight[i];

思考3：假如变成随意定点到某点的线权总合+某点的点权，程序应该怎么改？

解：

dfs(点的编号,0); 0代表时间从0开始递归

2.小红点点点

难度

知识点：dfs

开一个visited数组用来标记是否访问。对于每个没被访问过的红色节点，开始dfs并标记其相邻的红色节点。只要标号是从小到大开始遍历，最终形成的方案就一定是字典序最小的

题目描述：

小红拿到了一个图，其由 n个顶点、m 条边组成。

这个图上面的一些点被染成了红色。

小红有一个能力：她每次可以点击一个红色的顶点，并将和这个顶点相邻的红色连通块的所有红色顶点全部标记。

当两个红色顶点有一条边相连时，这两个红色顶点被称为连通的。另外，若a和b连通且b和c连通，那么a和c也是连通的。

小红想知道自己至少要点击多少次，可以把所有红色的顶点全部标记。

你能告诉她点击的次数吗？并请你输出一个点击的方案，如果有多个方案合法，请你输出一个字典序最小的方案。

注：字典序的定义：两个不同方案的字典序比较：对于从左到右数第一个不同的数，哪个方案最小，那么它的字典序最小。

例如：方案[1,4,5]和方案[1,3,6]相比，后者更小。因为第一个出现的不同的数是第二个数，4>3。

输入描述:

第一行输出两个正整数 n 和 m ，用空格隔开。分别代表顶点数和边数。

第二行输入一个长度为 n 的字符串，代表每个顶点的染色情况。第 i 个字符为'R'代表第 i 个点被染成红色，为'W'代表未被染色。

接下来的 m 行，每行两个正整数 x 和 y ，代表 x 和 y 有一条无向边相连。

不保证图是整体连通的。不保证没有重边和自环。

数据范围：

输出描述:

第一行输出一个正整数 cnt ，代表小红的点击次数。

第二行输出 cnt 个正整数，用空格隔开，代表小红点击的顺序。

示例1

输入

5 5

RRRWR

3 4

3 1

2 5

5 5

4 5

输出

2

1 2

说明

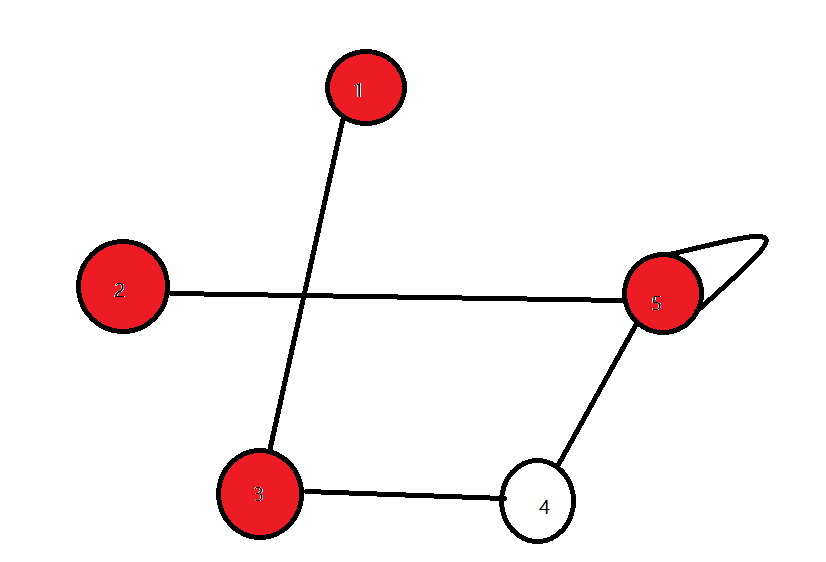
可以发现，共有2个红色连通块：{1,3}和{2,5}。只需要点击2次即可，字典序最小的方案是[1,2]

import java.util.*;
import java.io.*;

public class Main {
    static ArrayList<Integer>[] g;
    static String[] strings;
    static int[] visited;

    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String[] firstLine = br.readLine().split(" ");
        int n = Integer.parseInt(firstLine[0]);
        int m = Integer.parseInt(firstLine[1]);
        g = new ArrayList[n+1];
        visited = new int[n+1];
        for (int i=1;i<n+1;i++) {
            g[i] = new ArrayList<Integer>();
        }
        //一个字符一个字符的读取
        strings = br.readLine().split("");
        for (int i=0;i<m;i++) {
            //描绘双向图
            String[] temp = br.readLine().split(" ");
            int x = Integer.parseInt(temp[0]);
            int y = Integer.parseInt(temp[1]);
            g[x].add(y);
            g[y].add(x);
        }
        int cnt = 0;
        StringBuilder sb = new StringBuilder();
        for (int i=1;i<n+1;i++) {
            if (visited[i] ==0 && strings[i-1].equals("R")) {
                cnt++;
                sb.append(i + " ");
                //从糖葫芦小的开始纪录，然后延深。
                dfs(i);
            }
        }
        System.out.println(cnt);
        System.out.println(sb);
    }

    static void dfs(int x) {
        if (visited[x] ==0 && strings[x-1].equals("R")) {
            //点亮它
            visited[x] = 1;
            for (int i=0;i<g[x].size();i++) {
                dfs(g[x].get(i));
            }
        }
    }
}

3.kotori和素因子

难度

知识点：dfs(回溯法)

按照题意进行dfs即可。注意素因子的判重，可以使用set或者visited数组。

题目描述:

kotori拿到了一些正整数。她决定从每个正整数取出一个素因子。但是，kotori有强迫症，她不允许两个不同的正整数取出相同的素因子。

她想知道，最终所有取出的数的和的最小值是多少？

注：若a%k==0，则称k是a的因子。若一个数有且仅有两个因子，则称其是素数。显然1只有一个因子，不是素数。

输入描述:

第一行一个正整数n，代表kotori拿到正整数的个数。

第二行共有n个数ai，表示每个正整数的值。

保证不存在两个相等的正整数。

1<=n<=10

2<=ai<=1000

输出描述:

一个正整数，代表取出的素因子之和的最小值。若不存在合法的取法，则输出-1。

示例1

输入

4

12 15 28 22

输出

17

说明

分别取3，5，7，2，可保证取出的数之和最小

示例2

输入

5

4 5 6 7 8

输出

-1

备注:        1<=n<=10        2<=ai<=1000

import java.util.*;
import java.io.*;

public class Main{
    static boolean[] check = new boolean[2000];
    static int[] ai;
    static int n;
    static int min = Integer.MAX_VALUE;
    //判断是否为素数
    static boolean isPrime(int x){
        if(x<2) return false;
        //这是根据开根号的演化版本，提高了效率。
        for(int i=2;i*i<=x;i++){
            if(x%i==0)return false;
        }
        return true;
    }
    static void dfs(int index,int sum){
        if(index==n){
            min=Math.min(min,sum);
            return;
        }
        //查找这个数没有被占用的素因子。
        for(int i=2;i<=ai[index];i++){
            if(ai[index]%i==0&&check[i]==false&&isPrime(i)){
                check[i]=true;
                dfs(index+1,sum+i);
                //回溯的方法。
                check[i]=false;
            }
        }
    }
    public static void main(String[] args)throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        n = Integer.parseInt(br.readLine());
        String[] a = br.readLine().split(" ");
        //负责保存所有输入的数
        ai = new int[n];
        for(int i=0;i<n;i++){
            ai[i]=Integer.parseInt(a[i]);
        }
        dfs(0,0);
        System.out.println(min==Integer.MAX_VALUE ? -1:min);
        br.close();
    }
}

4.kotori和糖果

难度

知识点：记忆化搜索

正难则反，我们反向推理。

如果共有n个糖果：

• 若n为偶数，最后一次合并一定是两堆n/2合并最优。
• 若n为奇数，最后一次合并一定是一堆n/2和一堆n/2+1合并最优（合并的价值为1）。

所以得到递推式：f(n)=f(n/2)+f(n-n/2)+n%2

题目描述：

kotori共有n块糖果，每块糖果的初始状态是分散的，她想把这些糖果聚在一堆。但她每次只能把两堆糖果合并成一堆。

已知把两堆数量为a和b的糖果聚在一堆的代价是|a-b|。

kotori想知道，她把这n块糖果聚在一堆的最小代价是多少？

输入描述:

第一行是一个正整数T，代表数据组数。

第二行到第T+1行，每行一个非负整数n，代表kotori的糖果总数量。

输出描述:

每行一个整数，代表kotori需要花费的最小代价。

示例

输入

2

5

6

输出

2

2

说明

n=5时，kotori可以这样聚集糖果：

1 1 1 1 1

2 1 1 1

2 2 1

2 3

5

每一步的代价分别是0,0,1,1，总代价为2。

备注:

对于50%的数据，0<T≤100000, 0≤n≤100000

对于另外50%的数据，T=1 , 0≤n≤1e18（这个数据范围是为了为了让你动态规划做不了，上面的范围可以做）

import java.util.*;
import java.io.*;
public class Main{
    static HashMap<Long,Long> map = new HashMap<>();
    public static void main (String[] args) throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int num = Integer.parseInt(br.readLine());
        for(int i = 0; i<num; i++){
            System.out.println(recurse(Long.parseLong(br.readLine())));
        }
    }
    static long recurse(long num){
        if(num <= 1) return 0;
        //用于保存
        if(map.containsKey(num)) return map.get(num);
        long pay = recurse(num/2) + recurse(num-num/2) +num%2;
        map.put(num,pay);
        return pay;
    }
}

num%2的作用就是为了计数，且保存。

到此这篇关于例题详解Java dfs与记忆化搜索和分治递归算法的使用的文章就介绍到这了,更多相关Java 递归算法内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！