Python Counting Bloom Filter原理与实现详细介绍

目录

• 前言
• 原理
• 一、BF 为什么不支持删除
• 二、什么是 Counting Bloom Filter
• 三、Counter 大小的选择
• 简单的实现
• 总结

前言

标准的 Bloom Filter 是一种比较简单的数据结构，只支持插入和查找两种操作。在所要表达的集合是静态集合的时候，标准 Bloom Filter 可以很好地工作，但是如果要表达的集合经常变动，标准Bloom Filter的弊端就显现出来了，因为它不支持删除操作。这就引出来了本文要谈的 Counting Bloom Filter，后文简写为 CBF。

原理

一、BF 为什么不支持删除

BF 为什么不能删除元素？我们可以举一个例子来说明。

比如要删除集合中的成员 dantezhao，那么就会先用 k 个哈希函数对其计算，因为 dantezhao 已经是集合成员，那么在位数组的对应位置一定是 1，我们如要要删除这个成员 dantezhao，就需要把计算出来的所有位置上的 1 置为 0，即将 5 和 16 两位置为 0 即可。

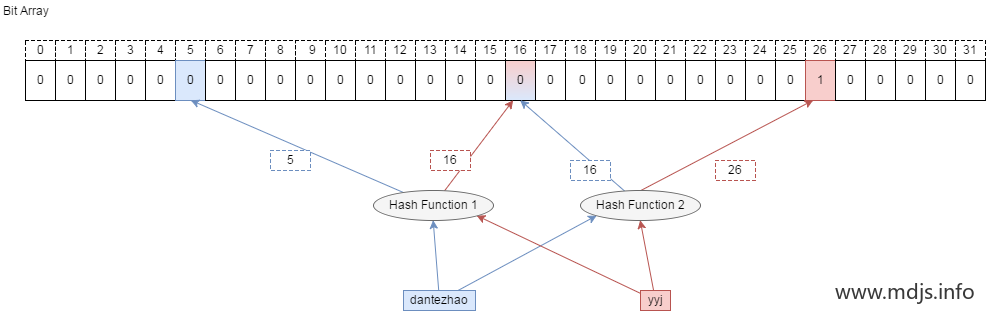
问题来了！现在，先假设 yyj 本身是属于集合的元素，如果需要查询 yyj 是否在集合中，通过哈希函数计算后，我们会去判断第 16 和 第 26 位是否为 1， 这时候就得到了第 16 位为 0 的结果，即 yyj 不属于集合。 显然这里是误判的。

二、什么是 Counting Bloom Filter

Counting Bloom Filter 的出现，解决了上述问题，它将标准 Bloom Filter 位数组的每一位扩展为一个小的计数器（Counter），在插入元素时给对应的 k （k 为哈希函数个数）个 Counter 的值分别加 1，删除元素时给对应的 k 个 Counter 的值分别减 1。Counting Bloom Filter 通过多占用几倍的存储空间的代价， 给 Bloom Filter 增加了删除操作。基本原理是不是很简单？看下图就能明白它和 Bloom Filter 的区别在哪。

三、Counter 大小的选择

CBF 和 BF 的一个主要的不同就是 CBF 用一个 Counter 取代了 BF 中的一位，那么 Counter 到底取多大才比较合适呢？这里就要考虑到空间利用率的问题了，从使用的角度来看，当然是越大越好，因为 Counter 越大就能表示越多的信息。但是越大的 Counter 就意味着更多的资源占用，而且在很多时候会造成极大的空间浪费。

因此，我们在选择 Counter 的时候，可以看 Counter 取值的范围多小就可以满足需求。

根据论文中描述，某一个 Counter 的值大于或等于 i 的概率可以通过如下公式描述，其中 n 为集合的大小，m 为 Counter 的数量，k 为 哈希函数的个数。

在之前的文章《Bloom Filter 的数学背景》中已经得出，k 的最佳取值为 k = m/n * ln2，将其带入公式后可得。

如果每个 Counter 分配 4 位，那么当 Counter 的值达到 16 时就会溢出。这个概率如下，这个值足够小，因此对于大多数应用程序来说，4位就足够了。

关于 CBF 中 Counter 大小的选择，主要参考这篇论文：《Summary Cache: A Scalable Wide-Area Web Cache Sharing Protocol》，在论文的第 6、7 两页专门对其做了一番阐述。这里不再推导细节，只给出一个大概的说明，感兴趣的童鞋可以参考原论文。

简单的实现

还是实现一个简单的程序来熟悉 CBF 的原理，这里和 BF 的区别有两个：

• 一个是我们没有用 bitarray 提供的位数组，而是使用了 bytearray 提供的一个 byte数组，因此每一个 Counter 的取值范围在 0~255。
• 另一个是多了一个 remove 方法来删除集合中的元素。

代码很简单，只是为了理解概念，实际中使用的库会有很大差别。

import mmh3
class CountingBloomFilter:
    def __init__(self, size, hash_num):
        self.size = size
        self.hash_num = hash_num
        self.byte_array = bytearray(size)
    def add(self, s):
        for seed in range(self.hash_num):
            result = mmh3.hash(s, seed) % self.size
            if self.bit_array[result] < 256:
                self.bit_array[result] += 1
    def lookup(self, s):
        for seed in range(self.hash_num):
            result = mmh3.hash(s, seed) % self.size
            if self.bit_array[result] == 0:
                return "Nope"
        return "Probably"
    def remove(self, s):
        for seed in range(self.hash_num):
            result = mmh3.hash(s, seed) % self.size
            if self.bit_array[result] > 0:
                self.bit_array[result] -= 1
cbf = CountingBloomFilter(500000, 7)
cbf.add("dantezhao")
cbf.add("yyj")
cbf.remove("dantezhao")
print (cbf.lookup("dantezhao"))
print (cbf.lookup("yyj"))

总结

CBF 虽说解决了 BF 的不能删除元素的问题，但是自身仍有不少的缺陷有待完善，比如 Counter 的引入就会带来很大的资源浪费，CBF 的 FP 还有很大可以降低的空间， 因此在实际的使用场景中会有很多 CBF 的升级版。

比如 SBF（Spectral Bloom Filter）在 CBF 的基础上提出了元素出现频率查询的概念，将CBF的应用扩展到了 multi-set 的领域；dlCBF（d-Left Counting Bloom Filter）利用 d-left hashing 的方法存储 fingerprint，解决哈希表的负载平衡问题；ACBF（Accurate Counting Bloom Filter）通过 offset indexing 的方式将 Counter 数组划分成多个层级，来降低误判率。这些内容，有机会再分享。

到此这篇关于Python Counting Bloom Filter原理与实现详细介绍的文章就介绍到这了,更多相关Python Counting Bloom Filter内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！