Android Matrix源码详解

Matrix的数学原理

在Android中，如果你用Matrix进行过图像处理，那么一定知道Matrix这个类。Android中的Matrix是一个3 x 3的矩阵，其内容如下：

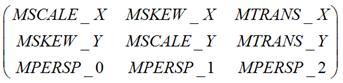
Matrix的对图像的处理可分为四类基本变换：

• Translate           平移变换
• Rotate                旋转变换
• Scale                  缩放变换
• Skew                  错切变换

从字面上理解，矩阵中的MSCALE用于处理缩放变换，MSKEW用于处理错切变换，MTRANS用于处理平移变换，MPERSP用于处理透视变换。实际中当然不能完全按照字面上的说法去理解Matrix。同时，在Android的文档中，未见到用Matrix进行透视变换的相关说明，所以本文也不讨论这方面的问题。

针对每种变换，Android提供了pre、set和post三种操作方式。其中

set用于设置Matrix中的值。

pre是先乘，因为矩阵的乘法不满足交换律，因此先乘、后乘必须要严格区分。先乘相当于矩阵运算中的右乘。

post是后乘，因为矩阵的乘法不满足交换律，因此先乘、后乘必须要严格区分。后乘相当于矩阵运算中的左乘。

除平移变换(Translate)外，旋转变换(Rotate)、缩放变换(Scale)和错切变换(Skew)都可以围绕一个中心点来进行，如果不指定，在默认情况下是围绕(0, 0)来进行相应的变换的。

下面我们来看看四种变换的具体情形。由于所有的图形都是有点组成，因此我们只需要考察一个点相关变换即可。

一、 平移变换

假定有一个点的坐标是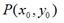 ，将其移动到 ，再假定在x轴和y轴方向移动的大小分别为：

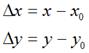
如下图所示：

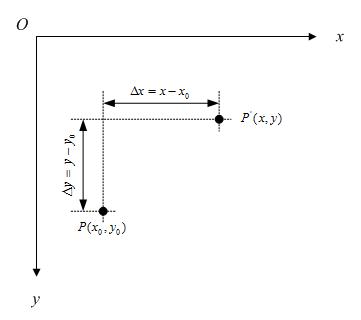
不难知道：

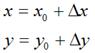
如果用矩阵来表示的话，就可以写成：

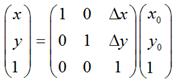
二、 旋转变换

2.1    围绕坐标原点旋转：

假定有一个点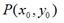 ，相对坐标原点顺时针旋转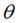后的情形，同时假定P点离坐标原点的距离为r，如下图：

那么，

如果用矩阵，就可以表示为：

2.2    围绕某个点旋转

如果是围绕某个点顺时针旋转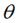，那么可以用矩阵表示为：

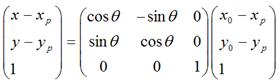
可以化为：

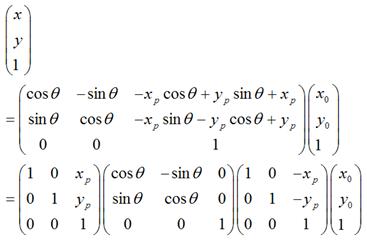
很显然，

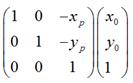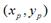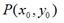1.  是将坐标原点移动到点后， 的新坐标。

2. 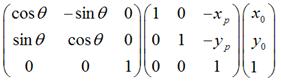    是将上一步变换后的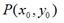，围绕新的坐标原点顺时针旋转 。

3.    

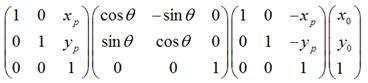
经过上一步旋转变换后，再将坐标原点移回到原来的坐标原点。

所以，围绕某一点进行旋转变换，可以分成3个步骤，即首先将坐标原点移至该点，然后围绕新的坐标原点进行旋转变换，再然后将坐标原点移回到原先的坐标原点。

三、 缩放变换

理论上而言，一个点是不存在什么缩放变换的，但考虑到所有图像都是由点组成，因此，如果图像在x轴和y轴方向分别放大k1和k2倍的话，那么图像中的所有点的x坐标和y坐标均会分别放大k1和k2倍，即

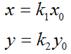
用矩阵表示就是：

缩放变换比较好理解，就不多说了。

 四、 错切变换

错切变换(skew)在数学上又称为Shear mapping(可译为“剪切变换”)或者Transvection(缩并)，它是一种比较特殊的线性变换。错切变换的效果就是让所有点的x坐标(或者y坐标)保持不变，而对应的y坐标(或者x坐标)则按比例发生平移，且平移的大小和该点到x轴(或y轴)的垂直距离成正比。错切变换，属于等面积变换，即一个形状在错切变换的前后，其面积是相等的。

比如下图，各点的y坐标保持不变，但其x坐标则按比例发生了平移。这种情况将水平错切。

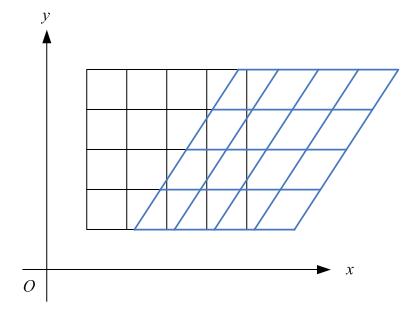
下图各点的x坐标保持不变，但其y坐标则按比例发生了平移。这种情况叫垂直错切。

假定一个点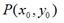经过错切变换后得到，对于水平错切而言，应该有如下关系：

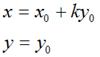
用矩阵表示就是：

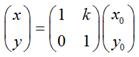
扩展到3 x 3的矩阵就是下面这样的形式：

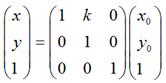
同理，对于垂直错切，可以有：

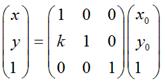
在数学上严格的错切变换就是上面这样的。在Android中除了有上面说到的情况外，还可以同时进行水平、垂直错切，那么形式上就是：

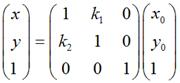
五、 对称变换

除了上面讲到的4中基本变换外，事实上，我们还可以利用Matrix，进行对称变换。所谓对称变换，就是经过变化后的图像和原图像是关于某个对称轴是对称的。比如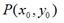，某点 经过对称变换后得到，

如果对称轴是x轴，难么，

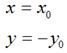
用矩阵表示就是：

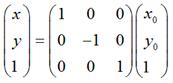
如果对称轴是y轴，那么，

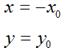
用矩阵表示就是：

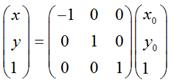
如果对称轴是y = x，如图：

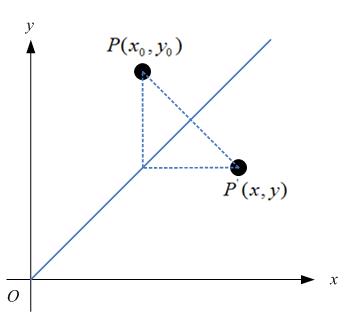
那么，

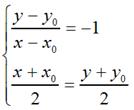
很容易可以解得：

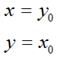
用矩阵表示就是：

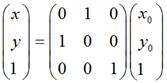
同样的道理，如果对称轴是y = -x，那么用矩阵表示就是：

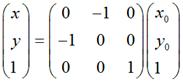
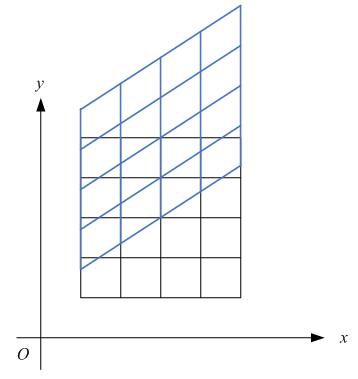
特殊地，如果对称轴是y = kx，如下图：

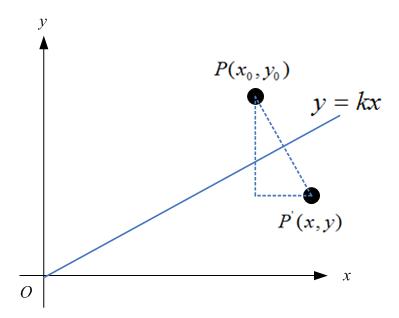
那么，

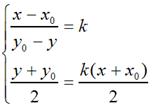
很容易可解得：

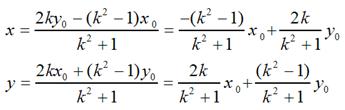
用矩阵表示就是：

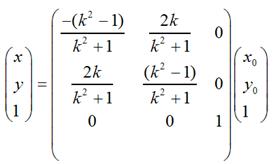
当k = 0时，即y = 0，也就是对称轴为x轴的情况；当k趋于无穷大时，即x = 0，也就是对称轴为y轴的情况；当k =1时，即y = x，也就是对称轴为y = x的情况；当k = -1时，即y = -x，也就是对称轴为y = -x的情况。不难验证，这和我们前面说到的4中具体情况是相吻合的。

如果对称轴是y = kx + b这样的情况，只需要在上面的基础上增加两次平移变换即可，即先将坐标原点移动到(0, b)，然后做上面的关于y = kx的对称变换，再然后将坐标原点移回到原来的坐标原点即可。用矩阵表示大致是这样的：

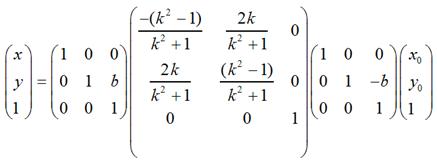
需要特别注意：在实际编程中，我们知道屏幕的y坐标的正向和数学中y坐标的正向刚好是相反的，所以在数学上y = x和屏幕上的y = -x才是真正的同一个东西，反之亦然。也就是说，如果要使图片在屏幕上看起来像按照数学意义上y = x对称，那么需使用这种转换：

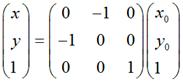
要使图片在屏幕上看起来像按照数学意义上y = -x对称，那么需使用这种转换：

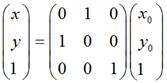
关于对称轴为y = kx 或y = kx + b的情况，同样需要考虑这方面的问题。

第二部分 代码验证

在第一部分中讲到的各种图像变换的验证代码如下，一共列出了10种情况。如果要验证其中的某一种情况，只需将相应的代码反注释即可。试验中用到的图片：

其尺寸为162 x 251。

每种变换的结果，请见代码之后的说明。

package compattesttransformmatrix;
import androidappActivity;
import androidcontentContext;
import androidgraphicsBitmap;
import androidgraphicsBitmapFactory;
import androidgraphicsCanvas;
import androidgraphicsMatrix;
import androidosBundle;
import androidutilLog;
import androidviewMotionEvent;
import androidviewView;
import androidviewWindow;
import androidviewWindowManager;
import androidviewViewOnTouchListener;
import androidwidgetImageView; 

public class TestTransformMatrixActivity extends Activity
implements
OnTouchListener
{
 private TransformMatrixView view;
 @Override
 public void onCreate(Bundle savedInstanceState)
 {
  superonCreate(savedInstanceState);
  requestWindowFeature(WindowFEATURE_NO_TITLE);
  thisgetWindow()setFlags(WindowManagerLayoutParamsFLAG_FULLSCREEN, WindowManagerLayoutParamsFLAG_FULLSCREEN); 

  view = new TransformMatrixView(this);
  viewsetScaleType(ImageViewScaleTypeMATRIX);
  viewsetOnTouchListener(this); 

  setContentView(view);
 } 

 class TransformMatrixView extends ImageView
 {
  private Bitmap bitmap;
  private Matrix matrix;
  public TransformMatrixView(Context context)
  {
   super(context);
   bitmap = BitmapFactorydecodeResource(getResources(), Rdrawablesophie);
   matrix = new Matrix();
  } 

  @Override
  protected void onDraw(Canvas canvas)
  {
   // 画出原图像
   canvasdrawBitmap(bitmap, 0, 0, null);
   // 画出变换后的图像
   canvasdrawBitmap(bitmap, matrix, null);
   superonDraw(canvas);
  } 

  @Override
  public void setImageMatrix(Matrix matrix)
  {
   thismatrixset(matrix);
   supersetImageMatrix(matrix);
  } 

  public Bitmap getImageBitmap()
  {
   return bitmap;
  }
 } 

 public boolean onTouch(View v, MotionEvent e)
 {
  if(egetAction() == MotionEventACTION_UP)
  {
   Matrix matrix = new Matrix();
   // 输出图像的宽度和高度(162 x 251)
   Loge("TestTransformMatrixActivity", "image size: width x height = " + viewgetImageBitmap()getWidth() + " x " + viewgetImageBitmap()getHeight());
   // 平移
   matrixpostTranslate(viewgetImageBitmap()getWidth(), viewgetImageBitmap()getHeight());
   // 在x方向平移viewgetImageBitmap()getWidth()，在y轴方向viewgetImageBitmap()getHeight()
   viewsetImageMatrix(matrix); 

   // 下面的代码是为了查看matrix中的元素
   float[] matrixValues = new float[9];
   matrixgetValues(matrixValues);
   for(int i = 0; i < 3; ++i)
   {
    String temp = new String();
    for(int j = 0; j < 3; ++j)
    {
     temp += matrixValues[3 * i + j ] + "\t";
    }
    Loge("TestTransformMatrixActivity", temp);
   } 

//   // 旋转(围绕图像的中心点)
//   matrixsetRotate(45f, viewgetImageBitmap()getWidth() / 2f, viewgetImageBitmap()getHeight() / 2f);
//
//   // 做下面的平移变换，纯粹是为了让变换后的图像和原图像不重叠
//   matrixpostTranslate(viewgetImageBitmap()getWidth() * 5f, 0f);
//   viewsetImageMatrix(matrix);
//
//   // 下面的代码是为了查看matrix中的元素
//   float[] matrixValues = new float[9];
//   matrixgetValues(matrixValues);
//   for(int i = 0; i < 3; ++i)
//   {
//    String temp = new String();
//    for(int j = 0; j < 3; ++j)
//    {
//     temp += matrixValues[3 * i + j ] + "\t";
//    }
//    Loge("TestTransformMatrixActivity", temp);
//   } 

//   // 旋转(围绕坐标原点) + 平移(效果同2)
//   matrixsetRotate(45f);
//   matrixpreTranslate(-1f * viewgetImageBitmap()getWidth() / 2f, -1f * viewgetImageBitmap()getHeight() / 2f);
//   matrixpostTranslate((float)viewgetImageBitmap()getWidth() / 2f, (float)viewgetImageBitmap()getHeight() / 2f);
//
//   // 做下面的平移变换，纯粹是为了让变换后的图像和原图像不重叠
//   matrixpostTranslate((float)viewgetImageBitmap()getWidth() * 5f, 0f);
//   viewsetImageMatrix(matrix);
//
//   // 下面的代码是为了查看matrix中的元素
//   float[] matrixValues = new float[9];
//   matrixgetValues(matrixValues);
//   for(int i = 0; i < 3; ++i)
//   {
//    String temp = new String();
//    for(int j = 0; j < 3; ++j)
//    {
//     temp += matrixValues[3 * i + j ] + "\t";
//    }
//    Loge("TestTransformMatrixActivity", temp);
//   }    

//   // 缩放
//   matrixsetScale(2f, 2f);
//   // 下面的代码是为了查看matrix中的元素
//   float[] matrixValues = new float[9];
//   matrixgetValues(matrixValues);
//   for(int i = 0; i < 3; ++i)
//   {
//    String temp = new String();
//    for(int j = 0; j < 3; ++j)
//    {
//     temp += matrixValues[3 * i + j ] + "\t";
//    }
//    Loge("TestTransformMatrixActivity", temp);
//   }
//
//   // 做下面的平移变换，纯粹是为了让变换后的图像和原图像不重叠
//   matrixpostTranslate(viewgetImageBitmap()getWidth(), viewgetImageBitmap()getHeight());
//   viewsetImageMatrix(matrix);
//
//   // 下面的代码是为了查看matrix中的元素
//   matrixValues = new float[9];
//   matrixgetValues(matrixValues);
//   for(int i = 0; i < 3; ++i)
//   {
//    String temp = new String();
//    for(int j = 0; j < 3; ++j)
//    {
//     temp += matrixValues[3 * i + j ] + "\t";
//    }
//    Loge("TestTransformMatrixActivity", temp);
//   } 

//   // 错切 - 水平
//   matrixsetSkew(5f, 0f);
//   // 下面的代码是为了查看matrix中的元素
//   float[] matrixValues = new float[9];
//   matrixgetValues(matrixValues);
//   for(int i = 0; i < 3; ++i)
//   {
//    String temp = new String();
//    for(int j = 0; j < 3; ++j)
//    {
//     temp += matrixValues[3 * i + j ] + "\t";
//    }
//    Loge("TestTransformMatrixActivity", temp);
//   }
//
//   // 做下面的平移变换，纯粹是为了让变换后的图像和原图像不重叠
//   matrixpostTranslate(viewgetImageBitmap()getWidth(), 0f);
//   viewsetImageMatrix(matrix);
//
//   // 下面的代码是为了查看matrix中的元素
//   matrixValues = new float[9];
//   matrixgetValues(matrixValues);
//   for(int i = 0; i < 3; ++i)
//   {
//    String temp = new String();
//    for(int j = 0; j < 3; ++j)
//    {
//     temp += matrixValues[3 * i + j ] + "\t";
//    }
//    Loge("TestTransformMatrixActivity", temp);
//   } 

//   // 错切 - 垂直
//   matrixsetSkew(0f, 5f);
//   // 下面的代码是为了查看matrix中的元素
//   float[] matrixValues = new float[9];
//   matrixgetValues(matrixValues);
//   for(int i = 0; i < 3; ++i)
//   {
//    String temp = new String();
//    for(int j = 0; j < 3; ++j)
//    {
//     temp += matrixValues[3 * i + j ] + "\t";
//    }
//    Loge("TestTransformMatrixActivity", temp);
//   }
//
//   // 做下面的平移变换，纯粹是为了让变换后的图像和原图像不重叠
//   matrixpostTranslate(0f, viewgetImageBitmap()getHeight());
//   viewsetImageMatrix(matrix);
//
//   // 下面的代码是为了查看matrix中的元素
//   matrixValues = new float[9];
//   matrixgetValues(matrixValues);
//   for(int i = 0; i < 3; ++i)
//   {
//    String temp = new String();
//    for(int j = 0; j < 3; ++j)
//    {
//     temp += matrixValues[3 * i + j ] + "\t";
//    }
//    Loge("TestTransformMatrixActivity", temp);
//   }    

//   错切 - 水平 + 垂直
//   matrixsetSkew(5f, 5f);
//   // 下面的代码是为了查看matrix中的元素
//   float[] matrixValues = new float[9];
//   matrixgetValues(matrixValues);
//   for(int i = 0; i < 3; ++i)
//   {
//    String temp = new String();
//    for(int j = 0; j < 3; ++j)
//    {
//     temp += matrixValues[3 * i + j ] + "\t";
//    }
//    Loge("TestTransformMatrixActivity", temp);
//   }
//
//   // 做下面的平移变换，纯粹是为了让变换后的图像和原图像不重叠
//   matrixpostTranslate(0f, viewgetImageBitmap()getHeight());
//   viewsetImageMatrix(matrix);
//
//   // 下面的代码是为了查看matrix中的元素
//   matrixValues = new float[9];
//   matrixgetValues(matrixValues);
//   for(int i = 0; i < 3; ++i)
//   {
//    String temp = new String();
//    for(int j = 0; j < 3; ++j)
//    {
//     temp += matrixValues[3 * i + j ] + "\t";
//    }
//    Loge("TestTransformMatrixActivity", temp);
//   } 

//   // 对称 (水平对称)
//   float matrix_values[] = {1f, 0f, 0f, 0f, -1f, 0f, 0f, 0f, 1f};
//   matrixsetValues(matrix_values);
//   // 下面的代码是为了查看matrix中的元素
//   float[] matrixValues = new float[9];
//   matrixgetValues(matrixValues);
//   for(int i = 0; i < 3; ++i)
//   {
//    String temp = new String();
//    for(int j = 0; j < 3; ++j)
//    {
//     temp += matrixValues[3 * i + j ] + "\t";
//    }
//    Loge("TestTransformMatrixActivity", temp);
//   }
//
//   // 做下面的平移变换，纯粹是为了让变换后的图像和原图像不重叠
//   matrixpostTranslate(0f, viewgetImageBitmap()getHeight() * 2f);
//   viewsetImageMatrix(matrix);
//
//   // 下面的代码是为了查看matrix中的元素
//   matrixValues = new float[9];
//   matrixgetValues(matrixValues);
//   for(int i = 0; i < 3; ++i)
//   {
//    String temp = new String();
//    for(int j = 0; j < 3; ++j)
//    {
//     temp += matrixValues[3 * i + j ] + "\t";
//    }
//    Loge("TestTransformMatrixActivity", temp);
//   }    

//   // 对称 - 垂直
//   float matrix_values[] = {-1f, 0f, 0f, 0f, 1f, 0f, 0f, 0f, 1f};
//   matrixsetValues(matrix_values);
//   // 下面的代码是为了查看matrix中的元素
//   float[] matrixValues = new float[9];
//   matrixgetValues(matrixValues);
//   for(int i = 0; i < 3; ++i)
//   {
//    String temp = new String();
//    for(int j = 0; j < 3; ++j)
//    {
//     temp += matrixValues[3 * i + j ] + "\t";
//    }
//    Loge("TestTransformMatrixActivity", temp);
//   }
//
//   // 做下面的平移变换，纯粹是为了让变换后的图像和原图像不重叠
//   matrixpostTranslate(viewgetImageBitmap()getWidth() * 2f, 0f);
//   viewsetImageMatrix(matrix);
//
//   // 下面的代码是为了查看matrix中的元素
//   matrixValues = new float[9];
//   matrixgetValues(matrixValues);
//   for(int i = 0; i < 3; ++i)
//   {
//    String temp = new String();
//    for(int j = 0; j < 3; ++j)
//    {
//     temp += matrixValues[3 * i + j ] + "\t";
//    }
//    Loge("TestTransformMatrixActivity", temp);
//   } 

//   // 对称(对称轴为直线y = x)
//   float matrix_values[] = {0f, -1f, 0f, -1f, 0f, 0f, 0f, 0f, 1f};
//   matrixsetValues(matrix_values);
//   // 下面的代码是为了查看matrix中的元素
//   float[] matrixValues = new float[9];
//   matrixgetValues(matrixValues);
//   for(int i = 0; i < 3; ++i)
//   {
//    String temp = new String();
//    for(int j = 0; j < 3; ++j)
//    {
//     temp += matrixValues[3 * i + j ] + "\t";
//    }
//    Loge("TestTransformMatrixActivity", temp);
//   }
//
//   // 做下面的平移变换，纯粹是为了让变换后的图像和原图像不重叠
//   matrixpostTranslate(viewgetImageBitmap()getHeight() + viewgetImageBitmap()getWidth(),
//     viewgetImageBitmap()getHeight() + viewgetImageBitmap()getWidth());
//   viewsetImageMatrix(matrix);
//
//   // 下面的代码是为了查看matrix中的元素
//   matrixValues = new float[9];
//   matrixgetValues(matrixValues);
//   for(int i = 0; i < 3; ++i)
//   {
//    String temp = new String();
//    for(int j = 0; j < 3; ++j)
//    {
//     temp += matrixValues[3 * i + j ] + "\t";
//    }
//    Loge("TestTransformMatrixActivity", temp);
//   } 

   viewinvalidate();
  }
  return true;
 }
}

下面给出上述代码中，各种变换的具体结果及其对应的相关变换矩阵

1.     平移

输出的结果：

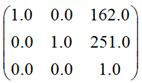
请对照第一部分中的“一、平移变换”所讲的情形，考察上述矩阵的正确性。

2.     旋转(围绕图像的中心点)

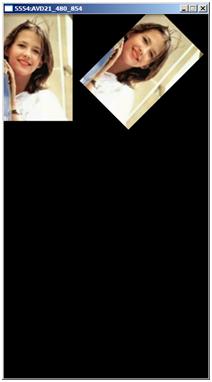
输出的结果：

它实际上是

matrix.setRotate(45f,view.getImageBitmap().getWidth() / 2f, view.getImageBitmap().getHeight() / 2f);

matrix.postTranslate(view.getImageBitmap().getWidth()* 1.5f, 0f);

这两条语句综合作用的结果。根据第一部分中“二、旋转变换”里面关于围绕某点旋转的公式，

matrix.setRotate(45f,view.getImageBitmap().getWidth() / 2f, view.getImageBitmap().getHeight() / 2f);

所产生的转换矩阵就是：

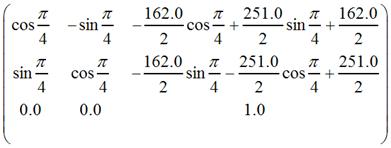
而matrix.postTranslate(view.getImageBitmap().getWidth()* 1.5f, 0f);的意思就是在上述矩阵的左边再乘以下面的矩阵：

关于post是左乘这一点，我们在前面的理论部分曾经提及过，后面我们还会专门讨论这个问题。

所以它实际上就是：

出去计算上的精度误差，我们可以看到我们计算出来的结果，和程序直接输出的结果是一致的。

3.     旋转(围绕坐标原点旋转，在加上两次平移，效果同2)

根据第一部分中“二、旋转变换”里面关于围绕某点旋转的解释，不难知道：

matrix.setRotate(45f,view.getImageBitmap().getWidth() / 2f, view.getImageBitmap().getHeight() / 2f);

等价于

matrix.setRotate(45f);

matrix.preTranslate(-1f* view.getImageBitmap().getWidth() / 2f, -1f *view.getImageBitmap().getHeight() / 2f);

matrix.postTranslate((float)view.getImageBitmap().getWidth()/ 2f, (float)view.getImageBitmap().getHeight() / 2f);

其中matrix.setRotate(45f)对应的矩阵是：

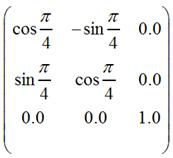
matrix.preTranslate(-1f* view.getImageBitmap().getWidth() / 2f, -1f * view.getImageBitmap().getHeight()/ 2f)对应的矩阵是：

由于是preTranslate，是先乘，也就是右乘，即它应该出现在matrix.setRotate(45f)所对应矩阵的右侧。

matrix.postTranslate((float)view.getImageBitmap().getWidth()/ 2f, (float)view.getImageBitmap().getHeight() / 2f)对应的矩阵是：

这次由于是postTranslate，是后乘，也就是左乘，即它应该出现在matrix.setRotate(45f)所对应矩阵的左侧。

所以综合起来，

matrix.setRotate(45f);

matrix.preTranslate(-1f* view.getImageBitmap().getWidth() / 2f, -1f *view.getImageBitmap().getHeight() / 2f);

matrix.postTranslate((float)view.getImageBitmap().getWidth()/ 2f, (float)view.getImageBitmap().getHeight() / 2f);

对应的矩阵就是：

这和下面这个矩阵(围绕图像中心顺时针旋转45度)其实是一样的：

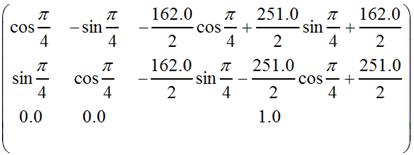
因此，此处变换后的图像和2中变换后的图像时一样的。

 4.     缩放变换

程序所输出的两个矩阵分别是：

其中第二个矩阵，其实是下面两个矩阵相乘的结果：

大家可以对照第一部分中的“三、缩放变换”和“一、平移变换”说法，自行验证结果。

5.     错切变换(水平错切)

代码所输出的两个矩阵分别是：

其中，第二个矩阵其实是下面两个矩阵相乘的结果：

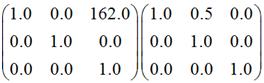
大家可以对照第一部分中的“四、错切变换”和“一、平移变换”的相关说法，自行验证结果。

 6.     错切变换(垂直错切)

代码所输出的两个矩阵分别是：

其中，第二个矩阵其实是下面两个矩阵相乘的结果：

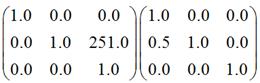
大家可以对照第一部分中的“四、错切变换”和“一、平移变换”的相关说法，自行验证结果。

7.     错切变换(水平+垂直错切)

代码所输出的两个矩阵分别是：

其中，后者是下面两个矩阵相乘的结果：

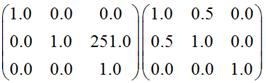
大家可以对照第一部分中的“四、错切变换”和“一、平移变换”的相关说法，自行验证结果。

8.     对称变换(水平对称)

代码所输出的两个各矩阵分别是：

其中，后者是下面两个矩阵相乘的结果：

大家可以对照第一部分中的“五、对称变换”和“一、平移变换”的相关说法，自行验证结果。

9.     对称变换(垂直对称)

代码所输出的两个矩阵分别是：

其中，后者是下面两个矩阵相乘的结果：

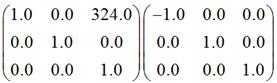
大家可以对照第一部分中的“五、对称变换”和“一、平移变换”的相关说法，自行验证结果。

10.   对称变换(对称轴为直线y = x)

代码所输出的两个矩阵分别是：

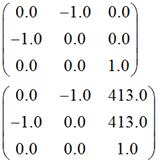
其中，后者是下面两个矩阵相乘的结果：

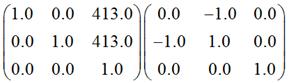
大家可以对照第一部分中的“五、对称变换”和“一、平移变换”的相关说法，自行验证结果。

 11.   关于先乘和后乘的问题

由于矩阵的乘法运算不满足交换律，我们在前面曾经多次提及先乘、后乘的问题，即先乘就是矩阵运算中右乘，后乘就是矩阵运算中的左乘。其实先乘、后乘的概念是针对变换操作的时间先后而言的，左乘、右乘是针对矩阵运算的左右位置而言的。以第一部分“二、旋转变换”中围绕某点旋转的情况为例：

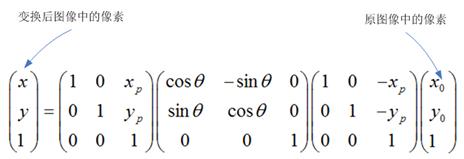
越靠近原图像中像素的矩阵，越先乘，越远离原图像中像素的矩阵，越后乘。事实上，图像处理时，矩阵的运算是从右边往左边方向进行运算的。这就形成了越在右边的矩阵(右乘)，越先运算(先乘)，反之亦然。

当然，在实际中，如果首先指定了一个matrix，比如我们先setRotate()，即指定了上面变换矩阵中，中间的那个矩阵，那么后续的矩阵到底是pre还是post运算，都是相对这个中间矩阵而言的。

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。