尾递归详细总结分析

一. 尾递归与Continuation

递归与尾递归
关于递归操作，相信大家都已经不陌生。简单地说，一个函数直接或间接地调用自身，是为直接或间接递归。例如，我们可以使用递归来计算一个单向链表的长度：


代码如下:

public class Node
{
    public Node(int value, Node next)
    {
        this.Value = value;
        this.Next = next;
    }

public int Value { get; private set; }

public Node Next { get; private set; }
}

编写一个递归的GetLength方法：


代码如下:

public static int GetLengthRecursively(Node head)
{
    if (head == null) return 0;
    return GetLengthRecursively(head.Next) + 1;
}

在调用时，GetLengthRecursively方法会不断调用自身，直至满足递归出口。对递归有些了解的朋友一定猜得到，如果单项链表十分长，那么上面这个方法就可能会遇到栈溢出，也就是抛出StackOverflowException。这是由于每个线程在执行代码时，都会分配一定尺寸的栈空间（Windows系统中为1M），每次方法调用时都会在栈里储存一定信息（如参数、局部变量、返回地址等等），这些信息再少也会占用一定空间，成千上万个此类空间累积起来，自然就超过线程的栈空间了。不过这个问题并非无解，我们只需把递归改成如下形式即可（在这篇文章里我们不考虑非递归的解法）：


代码如下:

public static int GetLengthTailRecursively(Node head, int acc)
{
    if (head == null) return acc;
    return GetLengthTailRecursively(head.Next, acc + 1);
}

GetLengthTailRecursively方法多了一个acc参数，acc的为accumulator（累加器）的缩写，它的功能是在递归调用时“积累”之前调用的结果，并将其传入下一次递归调用中——这就是GetLengthTailRecursively方法与GetLengthRecursively方法相比在递归方式上最大的区别：GetLengthRecursive方法在递归调用后还需要进行一次“+1”，而GetLengthTailRecursively的递归调用属于方法的最后一个操作。这就是所谓的“尾递归”。与普通递归相比，由于尾递归的调用处于方法的最后，因此方法之前所积累下的各种状态对于递归调用结果已经没有任何意义，因此完全可以把本次方法中留在堆栈中的数据完全清除，把空间让给最后的递归调用。这样的优化1便使得递归不会在调用堆栈上产生堆积，意味着即时是“无限”递归也不会让堆栈溢出。这便是尾递归的优势。

有些朋友可能已经想到了，尾递归的本质，其实是将递归方法中的需要的“所有状态”通过方法的参数传入下一次调用中。对于GetLengthTailRecursively方法，我们在调用时需要给出acc参数的初始值：


代码如下:

GetLengthTailRecursively(head, 0)

为了进一步熟悉尾递归的使用方式，我们再用著名的“菲波纳锲”数列作为一个例子。传统的递归方式如下：


代码如下:

public static int FibonacciRecursively(int n)
{
    if (n < 2) return n;
    return FibonacciRecursively(n - 1) + FibonacciRecursively(n - 2);
}

而改造成尾递归，我们则需要提供两个累加器：


代码如下:

public static int FibonacciTailRecursively(int n, int acc1, int acc2)
{
    if (n == 0) return acc1;
    return FibonacciTailRecursively(n - 1, acc2, acc1 + acc2);
}

于是在调用时，需要提供两个累加器的初始值：


代码如下:

FibonacciTailRecursively(10, 0, 1)

尾递归与Continuation
Continuation，即为“完成某件事情”之后“还需要做的事情”。例如，在.NET中标准的APM调用方式，便是由BeginXXX方法和EndXXX方法构成，这其实便是一种Continuation：在完成了BeginXXX方法之后，还需要调用EndXXX方法。而这种做法，也可以体现在尾递归构造中。例如以下为阶乘方法的传统递归定义：


代码如下:

public static int FactorialRecursively(int n)
{
    if (n == 0) return 1;
    return FactorialRecursively(n - 1) * n;
}

显然，这不是一个尾递归的方式，当然我们轻易将其转换为之前提到的尾递归调用方式。不过我们现在把它这样“理解”：每次计算n的阶乘时，其实是“先获取n - 1的阶乘”之后再“与n相乘并返回”，于是我们的FactorialRecursively方法可以改造成：


代码如下:

public static int FactorialRecursively(int n)
{
    return FactorialContinuation(n - 1, r => n * r);
}

// 6. FactorialContinuation(n, x => x)
public static int FactorialContinuation(int n, Func<int, int> continuation)
{
    ...
}

FactorialContinuation方法的含义是“计算n的阶乘，并将结果传入continuation方法，并返回其调用结果”。于是，很容易得出，FactorialContinuation方法自身便是一个递归调用：


代码如下:

public static int FactorialContinuation(int n, Func<int, int> continuation)
{
    return FactorialContinuation(n - 1,
        r => continuation(n * r));
}

FactorialContinuation方法的实现可以这样表述：“计算n的阶乘，并将结果传入continuation方法并返回”，也就是“计算n - 1的阶乘，并将结果与n相乘，再调用continuation方法”。为了实现“并将结果与n相乘，再调用continuation方法”这个逻辑，代码又构造了一个匿名方法，再次传入FactorialContinuation方法。当然，我们还需要为它补充递归的出口条件：


代码如下:

public static int FactorialContinuation(int n, Func<int, int> continuation)
{
    if (n == 0) return continuation(1);
    return FactorialContinuation(n - 1,
        r => continuation(n * r));
}

很明显，FactorialContinuation实现了尾递归。如果要计算n的阶乘，我们需要如下调用FactorialContinuation方法，表示“计算10的阶乘，并将结果直接返回”：


代码如下:

FactorialContinuation(10, x => x)

再加深一下印象，大家是否能够理解以下计算“菲波纳锲”数列第n项值的写法？


代码如下:

public static int FibonacciContinuation(int n, Func<int, int> continuation)
{
    if (n < 2) return continuation(n);
    return FibonacciContinuation(n - 1,
        r1 => FibonacciContinuation(n - 2,
            r2 => continuation(r1 + r2)));
}

在函数式编程中，此类调用方式便形成了“Continuation Passing Style（CPS）”。由于C#的Lambda表达式能够轻松构成一个匿名方法，我们也可以在C#中实现这样的调用方式。您可能会想——汗，何必搞得这么复杂，计算阶乘和“菲波纳锲”数列不是一下子就能转换成尾递归形式的吗？不过，您试试看以下的例子呢？

对二叉树进行先序遍历（pre-order traversal）是典型的递归操作，假设有如下TreeNode类：


代码如下:

public class TreeNode
{
    public TreeNode(int value, TreeNode left, TreeNode right)
    {
        this.Value = value;
        this.Left = left;
        this.Right = right;
    }

public int Value { get; private set; }

public TreeNode Left { get; private set; }

public TreeNode Right { get; private set; }
}

于是我们来传统的先序遍历一下：


代码如下:

public static void PreOrderTraversal(TreeNode root)
{
    if (root == null) return;

Console.WriteLine(root.Value);
    PreOrderTraversal(root.Left);
    PreOrderTraversal(root.Right);
}

您能用“普通”的方式将它转换为尾递归调用吗？这里先后调用了两次PreOrderTraversal，这意味着必然有一次调用没法放在末尾。这时候便要利用到Continuation了：


代码如下:

public static void PreOrderTraversal(TreeNode root, Action<TreeNode> continuation)
{
    if (root == null)
    {
        continuation(null);
        return;
    }

Console.WriteLine(root.Value);

PreOrderTraversal(root.Left,
        left => PreOrderTraversal(root.Right,
            right => continuation(right)));
}

我们现在把每次递归调用都作为代码的最后一次操作，把接下来的操作使用Continuation包装起来，这样就实现了尾递归，避免了堆栈数据的堆积。可见，虽然使用Continuation是一个略有些“诡异”的使用方式，但是在某些时候它也是必不可少的使用技巧。

Continuation的改进
看看刚才的先序遍历实现，您有没有发现一个有些奇怪的地方？


代码如下:

PreOrderTraversal(root.Left,
    left => PreOrderTraversal(root.Right,
        right => continuation(right)));

关于最后一步，我们构造了一个匿名函数作为第二次PreOrderTraversal调用的Continuation，但是其内部直接调用了continuation参数——那么我们为什么不直接把它交给第二次调用呢？如下：


代码如下:

PreOrderTraversal(root.Left,
    left => PreOrderTraversal(root.Right, continuation));

我们使用Continuation实现了尾递归，其实是把原本应该分配在栈上的信息丢到了托管堆上。每个匿名方法其实都是托管堆上的对象，虽然说这种生存周期短的对象不会对内存资源方面造成多大问题，但是尽可能减少此类对象，对于性能肯定是有帮助的。这里再举一个更为明显的例子，求二叉树的大小（Size）：


代码如下:

public static int GetSize(TreeNode root, Func<int, int> continuation)
{
    if (root == null) return continuation(0);
    return GetSize(root.Left,
        leftSize => GetSize(root.Right,
            rightSize => continuation(leftSize + rightSize + 1)));
}

GetSize方法使用了Continuation，它的理解方法是“获取root的大小，再将结果传入continuation，并返回其调用结果”。我们可以将其进行改写，减少Continuation方法的构造次数：


代码如下:

public static int GetSize2(TreeNode root, int acc, Func<int, int> continuation)
{
    if (root == null) return continuation(acc);
    return GetSize2(root.Left, acc,
        accLeftSize => GetSize2(root.Right, accLeftSize + 1, continuation));
}

GetSize2方法多了一个累加器参数，同时它的理解方式也有了变化：“将root的大小累加到acc上，再将结果传入continuation，并返回其调用结果”。也就是说GetSize2返回的其实是一个累加值，而并非是root参数的实际尺寸。当然，我们在调用时GetSize2时，只需将累加器置零便可：


代码如下:

GetSize2(root, 0, x => x)

不知您清楚了吗？

结束
在命令式编程中，我们解决一些问题往往可以使用循环来代替递归，这样便不会因为数据规模造成堆栈溢出。但是在函数式编程中，要实现“循环”的唯一方法便是“递归”，因此尾递归和CPS对于函数式编程的意义非常重大。了解尾递归，对于编程思维也有很大帮助，因此大家不妨多加思考和练习，让这样的方式为自己所用。

二. 浅谈尾递归的优化方式
在上文《尾递归与Continuation》里，我们谈到了尾递归的概念和示例，不过有些朋友对于尾递归的功效依然有所怀疑。因此现在，我再简单讲解一下尾递归的优化原理，希望能给大家以一定理性认识。

尾递归的循环优化
尾递归，即是递归调用放在方法末尾的递归方式，如经典的阶乘：


代码如下:

int FactorialTailRecursion(int n, int acc)
{
    if (n == 0) return acc;
    return FactorialTailRecursion(n - 1, acc * n);
}

由于递归在方法的末尾，因此方法中的局部变量已经毫无用处，编译器完全可以将其“复用”，并把尾递归优化为“循环”方式：


代码如下:

int FactorialLoopOptimized(int n, int acc)
{
    while (true)
    {
        if (n == 0) return acc;

acc *= n;
        n--;
    }
}

不过，上文还提到了尾递归中的常用技巧Continuation。那么对于如下形式的Continuation，编译器又该如何优化呢？


代码如下:

int FactorialContinuation(int n, Func<int, int> continuation)
{
    if (n == 0) return continuation(1);
    return FactorialContinuation(n - 1, r => continuation(n * r));
}

我们先用“人脑”来思考一下，这段代码的执行方式是怎么样的。我们每次使用n和contn调用FactorialContinuation时，都会构造一个新的contn - 1，并同n - 1传入下一次FactorialContinuation调用中去。以此类推，直到n等于0时，就直接调用cont0并返回。至于每个Continuation的定义，我们可以归纳出如下结果：


代码如下:

Func<int, int> contn = r => r * n

因此：


代码如下:

Factorial(n)
    = contn(contn - 1(...(cont2(cont1(cont0(1)))...))
    = n * ((n – 1) * (...(2 * (1 * 1))...)) =
    = n * (n - 1) * ... * 2 * 1
    = n!

于是，我们可以根据这个“意图”，将FactorialContinuation方法“优化”为如下形式：


代码如下:

int FactorialLoopOptimized2(int n, Func<int, int> continuation)
{
    LinkedList<Func<int, int>> contList = new LinkedList<Func<int, int>>();

while (true)
    {
        if (n == 0) break;

int tempN = n;
        Func<int, int> newCont = r => tempN * r;
        contList.AddFirst(newCont);

n--;
        continuation = newCont;
    }

return contList.Aggregate(1, (acc, cont) => cont(acc));
}

我们构造了一个Continuation函数链表，随着n递减，每次都会把新的Continuation函数插入到链表头，最后Aggregate方法会将第一个参数（累加器）依次运用到每个函数中去，得到最后结果并返回。只可惜，这个优化完全是我们“一厢情愿”而已，这么做的前提是“理解”了函数的意义，把方法的迭代调用“拆开”，而编译器是无法（还是很难）帮我们优化到如斯地步的。那么编译器对于此类问题又该如何解决呢？

之前，我们使用C#中的匿名方法特性来构造每个Continuation方法。如果我们使用自定义的封装类，再将递归“优化”成循环，FactorialContinuation又会成为什么样呢？如下：


代码如下:

private class Continuation
{
    public Continuation(Func<int, int> cont, int n)
    {
        this.cont = cont;
        this.n = n;
    }

private Func<int, int> cont;
    private int n;

public int Invoke(int r)
    {
        return this.cont(this.n * r);
    }
}

public static int FactorialLoopOptimized3(int n, Func<int, int> continuation)
{
    while (true)
    {
        if (n == 0) break;
        continuation = new Continuation(continuation, n).Invoke;
        n--;
    }

return continuation(1);
}

其实这才是FactorialContinuation的“直译”，也是编译器能够进行优化。不过朋友们应该也能够看出，这只是一个Continuation对象套着另一个Continuation对象。如果形成了数万个Continuation对象的嵌套，在最终调用最外层的Continuation时，每个内部的Continuation也会在调用时往同一个堆栈中不断累加，最终还是会造成堆栈溢出。因此，如果使用了Continuation，还是无法简单把递归优化成循环来避免堆栈溢出的。编译器还必须进行其他方面的优化。

方法尾调用的优化
上一篇文章曾经谈到：“与普通递归相比，由于尾递归的调用处于方法的最后，因此方法之前所积累下的各种状态对于递归调用结果已经没有任何意义，因此完全可以把本次方法中留在堆栈中的数据完全清除，把空间让给最后的递归调用。这样的优化便使得递归不会在调用堆栈上产生堆积，意味着即时是“无限”递归也不会让堆栈溢出”。这其实才是尾递归的“正统”优化方式，那么我们先暂时忘记之前的“循环优化”，从最简单的示例中查看这样的优化是如何进行的。还是最简单的“尾递归”阶乘：


代码如下:

static int FactorialTailRecursion(int n, int acc)
{
    if (n == 0) return acc;
    return FactorialTailRecursion(n - 1, acc * n);
}

它的IL代码是：


代码如下:

.method private hidebysig static int32 FactorialTailRecursion(int32 n, int32 acc) cil managed
{
    .maxstack 8
    L_0000: ldarg.0            // 加载第1个参数，即n
    L_0001: brtrue.s L_0005    // 如果第一个参数不为0，则跳转到L_0005
    L_0003: ldarg.1            // 运行到此，说明第1个参数为0，则加载第2个参数，即acc
    L_0004: ret                // 返回（刚加载的第2个参数）
    L_0005: ldarg.0            // 加载第1个参数，即n
    L_0006: ldc.i4.1           // 加载数值1
    L_0007: sub                // 将两者相减，即n - 1
    L_0008: ldarg.1            // 加载第2个参数，即acc
    L_0009: ldarg.0            // 加载第1个参数，即n
    L_000a: mul                // 将两者相乘，即acc * n
　　// 把n - 1和acc * n作为参数递归调用
    L_000b: call int32 TailRecursion.Recursion::FactorialTailRecursion(int32, int32)
    L_0010: ret                // 返回递归调用结果
}

在这个问题上，我们还需要观察它的汇编代码（为了不干扰文章内容，我会把获取汇编代码的做法单独写一篇文章，稍后发布），如下：


代码如下:

00ad00d0    push    ebp
00ad00d1    mov     ebp,esp
00ad00d3    push    esi
00ad00d4    mov     eax,edx
00ad00d6    test    ecx,ecx
00ad00d8    jne     00ad00dd
00ad00da    pop     esi
00ad00db    pop     ebp
00ad00dc    ret
00ad00dd    lea     edx,[ecx-1]
00ad00e0    imul    ecx,eax
00ad00e3    mov     esi,ecx
00ad00e5    test    edx,edx
00ad00e7    jne     00ad00ed
00ad00e9    mov     eax,esi
00ad00eb    jmp     00ad00f9
00ad00ed    lea     ecx,[edx-1]
00ad00f0    imul    edx,esi
00ad00f3    call    dword ptr ds:[703068h] (地址703068h的值即为00ad00d0)
00ad00f9    pop     esi
00ad00fa    pop     ebp
00ad00fb    ret

上面的汇编代码非常简单，从中可以看出，每次递归调用都使用了最简单的call指令，没有经过任何有效的优化或调整。因此在不断地递归调用之后，终究会出现堆栈溢出。这就是普通递归的缺陷。而对于尾递归来说，MSIL提供了额外的tail指令表示“尾调用”1，它只需简单补充在IL指令call, callvirt, calli之前便可。因此我们使用ildasm.exe将IL代码dump出来，并在call之前加上tail指令：


代码如下:

.method private hidebysig static int32 FactorialTailRecursion(int32 n, int32 acc) cil managed
{
    .maxstack 8
    L_0000: ldarg.0
    L_0001: brtrue.s L_0005
    L_0003: ldarg.1
    L_0004: ret
    L_0005: ldarg.0
    L_0006: ldc.i4.1
    L_0007: sub
    L_0008: ldarg.1
    L_0009: ldarg.0
    L_000a: mul
    L_000b: tail.
    L_000c: call int32 TailRecursion.Recursion::FactorialTailRecursion(int32, int32)
    L_0010: ret
}

使用ilasm.exe重新编译之后运行，再重新察看FactorialTailRecursion的汇编代码：


代码如下:

00a600d0    push    ebp
00a600d1    mov     ebp,esp
00a600d3    push    edi
00a600d4    push    esi
00a600d5    push    ebx
00a600d6    mov     eax,ecx
00a600d8    mov     esi,edx
00a600da    test    eax,eax
00a600dc    jne     00a600e5
00a600de    mov     eax,esi
00a600e0    pop     ebx
00a600e1    pop     esi
00a600e2    pop     edi
00a600e3    pop     ebp
00a600e4    ret
00a600e5    lea     ecx,[eax-1]
00a600e8    imul    eax,esi
00a600eb    mov     edx,eax
00a600ed    mov     eax,dword ptr ds:[813068h]
00a600f3    push    0
00a600f5    push    0
00a600f7    push    1
00a600f9    push    eax
00a600fa    cmp     dword ptr [mscorwks!g_TrapReturningThreads (7204339c)],0
00a60101    je      00a6010c
00a60103    push    ecx
00a60104    push    edx
00a60105    call    mscorwks!JIT_PollGC (71d5c9d3)
00a6010a    pop     edx
00a6010b    pop     ecx
00a6010c    call    mscorwks!JIT_TailCall (71b02890)
00a60111    int     3

在这里我实在无法完整讲述上述汇编代码的含义，不过从中可以看出它的确对于尾递归进行了特别的处理，而并非使用简单的call指令进行调用。对此互联网上的资源也不多，我只找到了Shri Borde的一篇文章，其中简单描述了Whidbey V2（真早）中CLR对于这方面的处理，以及一些相关的考虑，从中似乎能够看出一些苗头来。

让我们再回想之前的问题：Continuation无法通过简单优化为循环来解决递归问题。但是通过观察可以看出，Continuation.Invoke方法中的cont委托调用是最后一条命令，这说明它是一个“尾调用”——虽然不是“尾递归”，不过这已经满足tail指令的要求了：只需和所在方法返回值相同（或兼容）即可。因此，对于Continuation来说，我们也需要进行尾递归的优化。您可以进行尝试，现在无论递归多“深”，都不会使堆栈溢出了。

三.  尾递归对时间与空间复杂度的影响
以前我也在博客上简单谈过“尾递归”及其优化方式方面的话题。前几天有同学在写邮件向我提问，说是否所有的递归算法都能改写为尾递归，改写成尾递归之后，是否在时间和空间复杂度方面都能有所提高？他以斐波那契数列为例，似乎的确是这样的情况。我当时的回答有些简单，后来细想之后似乎感觉有点问题，而在仔细操作之后发现事情并没有理论上那么简单，

斐波那契数列
大家对于斐波那契数列（Fibonacci）的认识一定十分统一，唯一的区别可能仅在于n是从0开始还是从1开始算起。这里我们使用维基百科上的标准递归定义：

其边界情况为：
使用这个定义可以直接写出程序，这里我们用F#来表达：


代码如下:

let rec fib n =
    if n < 2 then n
    else fib (n - 1) + fib (n - 2)

这个算法最容易理解，但其时间复杂度确是：
这种指数级的时间复杂度在实际应用中是十分可怕的（虽然这个数字是美妙的黄金分割）。因此，我们如果真要“计算”斐波那契数列第n项的值（即不使用“通项公式”），则往往会使用迭代的方式进行，写作尾递归则是：


代码如下:

let fibTail n =
    // 第i项的值v1，以及即将累加上去的值v2
    let rec fibTail' i v1 v2 =
        if i >= n then v1
        else fibTail' (i + 1) (v1 + v2) v1
    fibTail' 0 0 1

从代码上也可以轻易地判断出，这个算法的时间复杂度是O(n)，实际上它也会被F#或是Scala等支持尾递归的编译器优化为循环操作。这里我们使用命令式编程语言C#来表达编译后的结果：


代码如下:

static int FibTail(int n, int i, int v1, int v2)
{
    while (i < n)
    {
        int temp = v1 + v2;
        v2 = v1;
        v1 = temp;
        i++;
    }

return v1;
}

时间复杂度从O(1.618n)降低到O(n)，可谓是质的飞跃。

尾调用对空间复杂度的影响
那么，在空间复杂度方面，尾递归带来什么优化吗？我们首先还是来分析标准的递归算法：

假设，我们知道，在一个（无副作用的）方法执行完毕之后，除了返回值以外的空间会完全释放出来，因此在fib(n - 2)执行结束之后，它的空间占用是常数级的。且fib(n - 1)的空间占用一定大于fib(n - 2)，假设其fib(n)的空间占用为S(n)，可得：

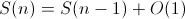
于是fib的空间复杂度是显而易见的O(n)。这个空间复杂度其实并不大，例如经典的归并排序算法的空间复杂度也同样是O(n)。但不幸的是，这里的递归操作占用的完全是栈空间，而栈空间的大小是极其有限的（例如一个Windows应用程序默认情况下只有1M，ASP.NET甚至只有250K）。因此，只需一个稍大一点的数字会产生栈溢出。经试验，在我的机器上只需51K便能出现StackOverflowException：


代码如下:

// 50K不会出现StackOverflowException
51 * 1024 |> fib |> printfn "%d"

那么尾递归算法的空间复杂度呢？我们刚才提到，编译器会将尾递归优化成循环，那在实际运行时这个算法的空间复杂度自然是常数级，即O(1)。但这是我们实际观察到的编译器优化后的结果，从理论上说，我们并无法保证这里的尾递归会被优化成循环。因此我们不妨也从“字面”上来理解代码，看看理论上这样的尾递归调用会形成怎样的空间占用。

对于尾递归来说，理论上我们只能期待它形成“尾调用”。也就是说，针对某个方法的调用（无论是否是递归操作）是父方法的最后一个操作。在这个情况下，我们无需保留父方法当前的栈空间，因此可以将其完全释放。于是，无论调用多少次，只要每次都将栈空间释放（或重用），其空间占用也始终是个常数，即O(1)。

因此，无论从理论上（从字面上分析）还是实际上（观察编译结果）来说，似乎将斐波那契数列修改为尾递归，能显著地降低时间及空间复杂度，这也是那位同学提出“尾递归能改进时间和空间复杂度”的依据。那么我们重新回顾一下文章开头所提出的两个问题：

每个递归算法都能改写为尾递归吗？

改写为尾递归都能改进时间及空间复杂度吗？