Python计算标准差之numpy.std和torch.std的区别

目录
  • 输入：
  • 课本中的标准差计算公式：
  • Numpy中的std计算：
  • Torch中的std计算：
  • 附：贝塞尔校正
  • 总结：

输入：

[1.0000, -1.0000, 3.0000]

课本中的标准差计算公式：

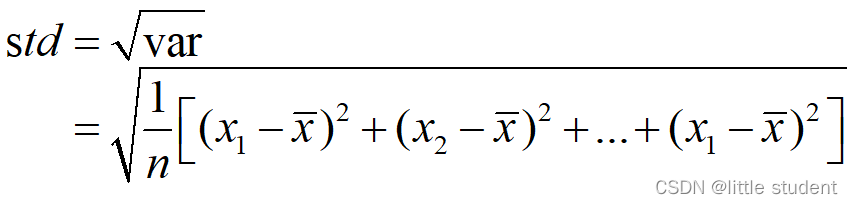
按照上述公式计算：

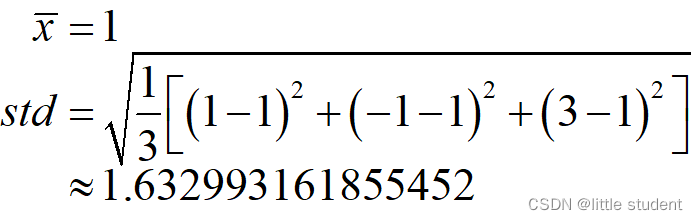
Numpy中的std计算：

import numpy as np

tm = np.array([1.0000, -1.0000, 3.0000])
ddd = np.std(tm)
print(ddd)

1.632993161855452

可以看出Numpy中的计算结果与课本中的公式计算出来的结果是一致的。

Torch中的std计算：

tm = torch.tensor([1.0000, -1.0000, 3.0000])
ddd = torch.std(tm)
print(ddd)

tensor(2.)

计算出来的结果是2，与Numpy中的计算结果是不相同的。

查看torch.std的参数：

torch.std默认设置了unbiased=True。此时计算标准差的公式则使用贝塞尔校正 的方法：

可以看出贝塞尔校正的标准差最后除以n - 1。

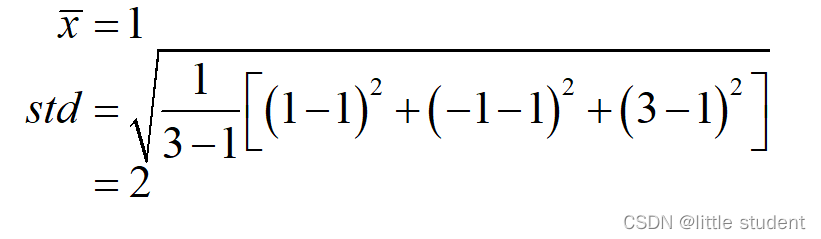
可以看出确实计算出来的结果是2.

至于为何使用n-1，这里不做过多介绍，建议参考：贝塞尔校正。

附：贝塞尔校正

贝塞尔校正，指的是样本方差前面的系数1/n-1

这就是这个系数的原理

注：设置torch.std中的unbiased=False，则与Numpy中的std的结果相同的。

总结：

Numpy中的std计算与课本中的计算方式相同，都是除的是样本数量n。

Torch中的std计算默认使用的是unbiased=True即贝塞尔校正，除的是样本数量n-1。

赞 (0)

相关推荐

  • numpy.std() 计算矩阵标准差的方法

    计算矩阵标准差 >>> a = np.array([[1, 2], [3, 4]]) >>> np.std(a) # 计算全局标准差 1.1180339887498949 >>> np.std(a, axis=0) # axis=0计算每一列的标准差 array([ 1., 1.]) >>> np.std(a, axis=1) # 计算每一行的标准差 array([ 0.5, 0.5]) 官方手册:http://docs.scipy.

  • Python计算标准差之numpy.std和torch.std的区别

    Python计算标准差之numpy.std和torch.std的区别

    目录 输入: 课本中的标准差计算公式: Numpy中的std计算: Torch中的std计算: 附:贝塞尔校正 总结: 输入: [1.0000, -1.0000, 3.0000] 课本中的标准差计算公式: 按照上述公式计算: Numpy中的std计算: import numpy as np tm = np.array([1.0000, -1.0000, 3.0000]) ddd = np.std(tm) print(ddd) 1.632993161855452 可以看出Numpy中的计算结果与课

  • 关于Python常用函数中NumPy的使用

    目录 1. txt文件 2. CSV文件 3.成交量加权平均价格 = average()函数 4. 算数平均值函数 = mean()函数 5. 时间加权平均价格 6. 最大值和最小值 7. 统计分析 8. 股票收益率 1. txt文件 (1) 单位矩阵 即主对角线上的元素均为1,其余元素均为0的正方形矩阵. 在NumPy中可以用eye函数创建一个这样的二维数组,我们只需要给定一个参数,用于指定矩阵中1的元素个数. 例如,创建3×3的数组: import numpy as np I2 = np.e

  • NumPy 与 Python 内置列表计算标准差区别详析

    NumPy 与 Python 内置列表计算标准差区别详析

    目录 1 什么是 Numpy 2 NumPy 数组和 Python 内置计算对比 3 函数计算时间装饰器 4 标准差计算公式 5 总结 1 什么是 Numpy NumPy,是 Numerical Python 的简称,用于高性能科学计算和数据分析的基础包,像数学科学工具(pandas)和框架(Scikit-learn)中都使用到了 NumPy 这个包. NumPy 中的基本数据结构是ndarray或者 N 维数值数组,在形式上来说,它的结构有点像 Python 的基础类型——Python列表.

  • Python计算库numpy进行方差/标准方差/样本标准方差/协方差的计算

    使用numpy可以做很多事情,在这篇文章中简单介绍一下如何使用numpy进行方差/标准方差/样本标准方差/协方差的计算. variance: 方差 方差(Variance)是概率论中最基础的概念之一,它是由统计学天才罗纳德·费雪1918年最早所提出.用于衡量数据离散程度,因为它能体现变量与其数学期望(均值)之间的偏离程度.具有相同均值的数据,而标准差可能不同,而通过标准差的大小则能更好地反映出数据的偏离度. 计算:一组数据1,2,3,4,其方差应该是多少? 计算如下: 均值=(1+2+3+4)/

  • 基于python计算滚动方差(标准差)talib和pd.rolling函数差异详解

    我就废话不多说了,大家还是直接看代码吧! # -*- coding: utf-8 -*- """ Created on Thu Apr 12 11:23:46 2018 @author: henbile """ #计算滚动波动率可以使用专门做技术分析的talib包里面的函数,也可以使用pandas包里面的滚动函数. #但是两个函数对于分母的选择,就是使用N还是N-1作为分母这件事情上是有分歧的. #另一个差异在于:talib包计算基于numpy,

  • 使用python计算方差方式——pandas.series.std()

    目录 如何计算方差 Python计算方差.标准差 方差.标准差 1.方差 2.标准差 如何计算方差 简单展示一下pandas里怎么计算方差: 官方文档: def def_std(df):   for ix,row in df.iterrows():     std = row.std()     df.loc[ix,"std"] = std   return df Python计算方差.标准差 方差.标准差 1.离散程度的测度值之一 2.最常用的测度值 3.反应了数据的分布 4.反应了

  • Python中11种NumPy高级操作总结

    Python中11种NumPy高级操作总结

    目录 1.数组上的迭代 2.数组形状修改函数 1.ndarray.reshape 2.ndarray.flat 3.ndarray.flatten 3.数组翻转操作函数 1.numpy.transpose 2. numpy.ndarray.T 3.numpy.swapaxes 4.numpy.rollaxis 4.数组修改维度函数 1.numpy.broadcast_to 2.numpy.expand_dims 3.numpy.squeeze 5.数组的连接操作 1.numpy.stack 2.

  • python 计算概率密度、累计分布、逆函数的例子

    计算概率分布的相关参数时,一般使用 scipy 包,常用的函数包括以下几个: pdf:连续随机分布的概率密度函数 pmf:离散随机分布的概率密度函数 cdf:累计分布函数 百分位函数(累计分布函数的逆函数) 生存函数的逆函数(1 - cdf 的逆函数) 函数里面不仅能跟一个数据,还能跟一个数组.下面用正态分布举例说明: >>> import scipy.stats as st >>> st.norm.cdf(0) # 标准正态分布在 0 处的累计分布概率值 0.5 &g

  • python计算方程式根的方法

    本文实例讲述了python计算方程式根的方法.分享给大家供大家参考.具体实现方法如下: ''' roots = polyRoots(a). Uses Laguerre's method to compute all the roots of a[0] + a[1]*x + a[2]*x^2 +...+ a[n]*x^n = 0. The roots are returned in the array 'roots', ''' from evalPoly import * from numpy i

  • python计算auc指标实例

    1.安装scikit-learn 1.1Scikit-learn 依赖 Python (>= 2.6 or >= 3.3), NumPy (>= 1.6.1), SciPy (>= 0.9). 分别查看上述三个依赖的版本, python -V 结果:Python 2.7.3 python -c 'import scipy; print scipy.version.version' scipy版本结果:0.9.0 python -c "import numpy; print

随机推荐