Blender Python编程实现程序化建模生成超形示例详解

目录

• 正文
• 什么是超形（Supershapes, Superformula）
• 二维超形
• n1 = n2 = n3 = 1
• n1 = n2 = n3 = 0.3
• 其他特别情况
• 例子 1
• 例子 2
• 例子 3
• 例子 4
• 例子 5
• 奇异的形状
• 三维超形
• Blender 生成超形
• 详细代码和注释如下

正文

Blender 并不是唯一一款允许你为场景编程和自动化任务的3D软件; 随着每一个新版本的推出，Blender 正逐渐成为一个可靠的 CG 制作一体化解决方案，从使用油脂铅笔的故事板到基于节点的合成。

事实上，你可以使用 Python 脚本和一些额外的包来批处理你的对象实例化，程序化地生成东西，配置你的渲染设置，甚至获得你当前项目的自定义统计数据，这是非常棒的功能! 这是一种减轻繁琐任务负担的方式，同时也能让开发者参与到这个创造性工具社区中，而不仅仅是美术人员。

什么是超形（Supershapes, Superformula）

截图来自于 ShaderToy

二维超形

超形方程是基于由 Johan Gielis 意图作为 自然形状的建模框架 而提出的。 二维超形方程是圆方程和椭圆方程的推广

他们给出的二维超椭圆/超形的一般公式如下。

其中 r 和 phi 是极坐标(表示半径、角度)

n1、n2、n3、m 都是实数。

a 和 b 是除 0 以外的实数。

m = 0 的话，结果就是圆，即 r = 1

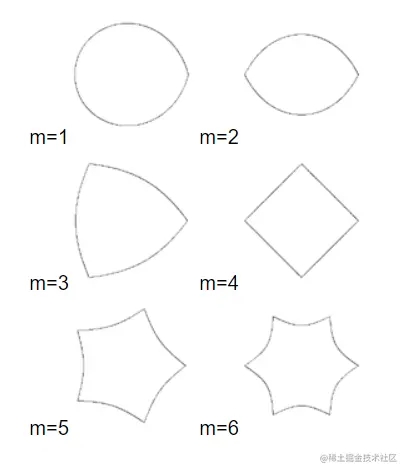
n1 = n2 = n3 = 1

增大 m 的话会增加形状的旋转对称性。这通常适用于对于 n 个参数为其他值时的情况。这些曲线在角 2π/m 的圆上重复出现，这现象在下面大多数 m 为整数值的例子中尤为明显。

n1 = n2 = n3 = 0.3

当 n 保持相等但减小时，形状将变得越来越紧凑。

其他特别情况

例子 1

如果 n1 略大于 n2 和 n3，则会形成 膨胀 的形式。

下边的例子有 n1 = 40 和 n2 = n3 = 10 。

例子 2

多边形 形状是用非常大的 n1 值以及虽然值大但相等的 n2 和 n3来实现的。

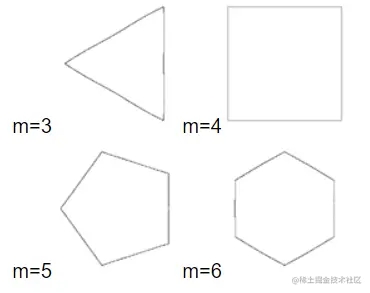
例子 3

不对称 形状可以通过使用不同的 n 值来创建。下面的例子有 n1 = 60, n2 = 55 和 n3 = 30。

例子 4

对于 m 的非整值，对于有理值其所生成的形状仍然是封闭的。下面是 n1 = n2 = n3 = 0.3 的示例。角度需要从 0 扩展到 12π 。

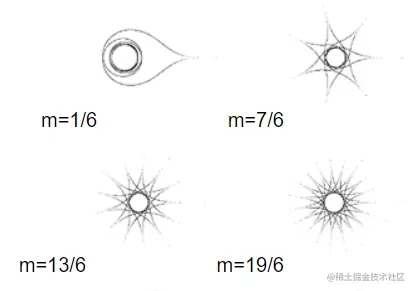
例子 5

由于 n1 的值小于 n2 和 n3，因此形成了光滑的海星形状。下面的例子有 m=5 和 n2 = n3 = 1.7 。

奇异的形状

感兴趣的朋友还可以尝试其他不同的形状

三维超形

在给出了上面二维超形的定义后，

我们可以使用球形乘积（spherical product）扩展到 3D 使用。

Blender 生成超形

有了以上的理论支持，我们就可以在 Blender 里面开始编写 Python 代码了，原理并不难，我们只需要套用上面的三维超形公式，然后定义我们自己的参数即可。

详细代码和注释如下

import bpy
import math
# mesh 数组（点、面、边）
verts = []
faces = []
edges = []
#3D supershape 参数
m = 14.23
a = -0.06
b = 2.78
n1 = 0.5
n2 = -.48
n3 = 1.5
scale = 3
Unum = 50
Vnum = 50
Uinc = math.pi / (Unum/2)
Vinc = (math.pi/2)/(Vnum/2)
# 套用公式，填充顶点数组
theta = -math.pi
for i in range (0, Unum + 1):
   phi = -math.pi/2
   r1 = 1/(((abs(math.cos(m*theta/4)/a))**n2+(abs(math.sin(m*theta/4)/b))**n3)**n1)
   for j in range(0,Vnum + 1):
       r2 = 1/(((abs(math.cos(m*phi/4)/a))**n2+(abs(math.sin(m*phi/4)/b))**n3)**n1)
       x = scale * (r1 * math.cos(theta) * r2 * math.cos(phi))
       y = scale * (r1 * math.sin(theta) * r2 * math.cos(phi))
       z = scale * (r2 * math.sin(phi))
       vert = (x,y,z)
       verts.append(vert)
       #增加 phi
       phi = phi + Vinc
   #增加 theta
   theta = theta + Uinc
# -------------------------------------------------------------------------------
# 填充面数组
count = 0
for i in range (0, (Vnum + 1) *(Unum)):
    if count < Vnum:
        A = i
        B = i+1
        C = (i+(Vnum+1))+1
        D = (i+(Vnum+1))
        face = (A,B,C,D)
        faces.append(face)
        count = count + 1
    else:
        count = 0
# 创建 mesh 和 object
mymesh = bpy.data.meshes.new("supershape")
myobject = bpy.data.objects.new("supershape",mymesh)
# 设置 mesh 的 location
myobject.location = bpy.context.scene.cursor.location # *
bpy.context.scene.collection.objects.link(myobject) # *
# 从 python 数据创建 mesh
mymesh.from_pydata(verts,edges,faces)
mymesh.update(calc_edges=True)
# 设置 object 为编辑模式
bpy.context.view_layer.objects.active = myobject # *
bpy.ops.object.mode_set(mode='EDIT')
# 移除重复的顶点
bpy.ops.mesh.remove_doubles()
# 重新计算法线
bpy.ops.mesh.normals_make_consistent(inside=False)
bpy.ops.object.mode_set(mode='OBJECT')
# 新建细分修改器（subdivide modifier）
myobject.modifiers.new("subd", type='SUBSURF')
myobject.modifiers['subd'].levels = 3
# 平滑 mesh
mypolys = mymesh.polygons
for p in mypolys:
    p.use_smooth = True

通过以上代码，我们就可以轻松生成如下形状，不用费力得进行 “雕刻”

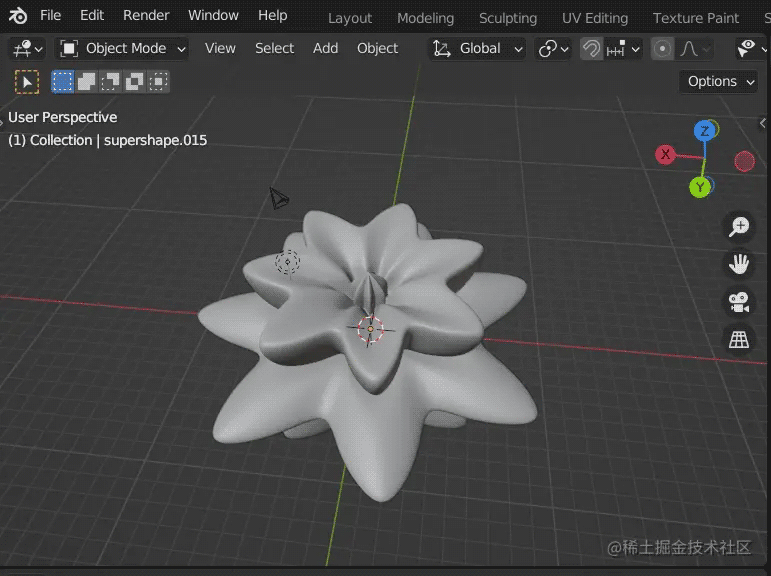
还可以自行修改参数，比如 “咻得一下” 就可以得到以下形状，是不是很简单~

以上就是Blender Python编程实现程序化建模生成超形示例详解的详细内容，更多关于Blender Python超形建模的资料请关注我们其它相关文章！