python数据预处理方式 :数据降维

数据为何要降维

数据降维可以降低模型的计算量并减少模型运行时间、降低噪音变量信息对于模型结果的影响、便于通过可视化方式展示归约后的维度信息并减少数据存储空间。因此，大多数情况下，当我们面临高维数据时，都需要对数据做降维处理。

数据降维有两种方式：特征选择，维度转换

特征选择

特征选择指根据一定的规则和经验，直接在原有的维度中挑选一部分参与到计算和建模过程，用选择的特征代替所有特征，不改变原有特征，也不产生新的特征值。

特征选择的降维方式好处是可以保留原有维度特征的基础上进行降维，既能满足后续数据处理和建模需求，又能保留维度原本的业务含义，以便于业务理解和应用。对于业务分析性的应用而言，模型的可理解性和可用性很多时候要有限于模型本身的准确率、效率等技术指标。例如，决策树得到的特征规则，可以作为选择用户样本的基础条件，而这些特征规则便是基于输入的维度产生。

维度转换

这个是按照一定数学变换方法，把给定的一组相关变量（维度）通过数学模型将高纬度空间的数据点映射到低纬度空间中，然后利用映射后变量的特征来表示原有变量的总体特征。这种方式是一种产生新维度的过程，转换后的维度并非原来特征，而是之前特征的转化后的表达式，新的特征丢失了原有数据的业务含义。 通过数据维度变换的降维方法是非常重要的降维方法，这种降维方法分为线性降维和非线性降维两种，其中常用的代表算法包括独立成分分析（ICA），主成分分析（PCA），因子分析（Factor Analysis，FA），线性判别分析（LDA），局部线性嵌入（LLE），核主成分分析（Kernel PCA）等。

使用python做降维处理

import pandas as pd
import numpy as np
from sklearn.tree import DecisionTreeClassifier
from sklearn.decomposition import PCA

# 数据导入
df = pd.read_csv('https://raw.githubusercontent.com/ffzs/dataset/master/glass.csv')

# 看一下数据是
df.head()

   RI   Na Mg Al   Si   K   Ca   Ba   Fe  Type
0 1.52101 13.64 4.49 1.10 71.78 0.06 8.75 0.0 0.0 1
1 1.51761 13.89 3.60 1.36 72.73 0.48 7.83 0.0 0.0 1
2 1.51618 13.53 3.55 1.54 72.99 0.39 7.78 0.0 0.0 1
3 1.51766 13.21 3.69 1.29 72.61 0.57 8.22 0.0 0.0 1
4 1.51742 13.27 3.62 1.24 73.08 0.55 8.07 0.0 0.0 1

# 有无缺失值
df.isna().values.any()
# False 没有缺失值

# 获取特征值
X = df.iloc[:, :-1].values
# 获取标签值
Y = df.iloc[:,[-1]].values
# 使用sklearn 的DecisionTreeClassifier判断变量重要性
# 建立分类决策树模型对象
dt_model = DecisionTreeClassifier(random_state=1)
# 将数据集的维度和目标变量输入模型
dt_model.fit(X, Y)
# 获取所有变量的重要性
feature_importance = dt_model.feature_importances_
feature_importance
# 结果如下
# array([0.20462132, 0.06426227, 0.16799114, 0.15372793, 0.07410088, 0.02786222, 0.09301948, 0.16519298, 0.04922178])
# 做可视化
import matplotlib.pyplot as plt

x = range(len(df.columns[:-1]))
plt.bar(left= x, height=feature_importance)
plt.xticks(x, df.columns[:-1])

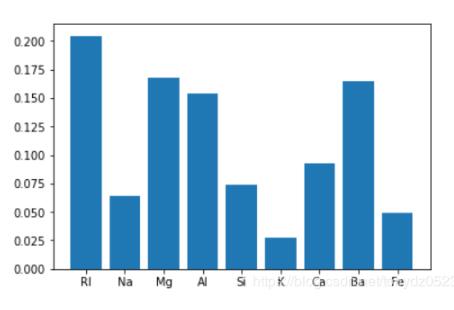
可见Rl、Mg、Al、Ba的重要性比较高，一般情况下变量重要性得分接近80%，基本上已经可以解释大部分的特征变化。

PCA降维

# 使用sklearn的PCA进行维度转换
# 建立PCA模型对象 n_components控制输出特征个数
pca_model = PCA(n_components=3)
# 将数据集输入模型
pca_model.fit(X)
# 对数据集进行转换映射
pca_model.transform(X)
# 获得转换后的所有主成分
components = pca_model.components_
# 获得各主成分的方差
components_var = pca_model.explained_variance_
# 获取主成分的方差占比
components_var_ratio = pca_model.explained_variance_ratio_
# 打印方差
print(np.round(components_var,3))
# [3.002 1.659 0.68 ]
# 打印方差占比
print(np.round(components_var_ratio,3))
# [0.476 0.263 0.108]

以上这篇python数据预处理方式 :数据降维就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持我们。