C++项目基于HuffmanTree实现文件的压缩与解压缩功能

目录

• 前言
• 一、文件压缩
• 1.文件压缩的概念
• 2.为什么需要压缩
• 3.压缩的分类
• 4.压缩的方法
• 二、HuffmanTree文件压缩与解压缩
• 1.HuffmanTree的概念
• 2.HuffmanTree的构建
• 3.文件压缩
• 4.文件解压缩
• 三、HuffmanTree压缩解压缩碰到的问题
• 1.创建优先级队列要使用自己写的仿函数
• 2.自定义类型结构体类型相加和仿函数要重载operator+和operator>
• 3.剔除在HuffmanTree出现0次的字符，不用统计出现0次的字符
• 4.如果在解压缩时，最后一个字节的压缩数据不满8个比特位，则在解压缩过程中如何处理？
• 5.在解压缩源文件中有汉字，解压缩过时出现乱码，怎么处理？
• 6.文件中包含多行文本时解压缩出现乱码
• 四、测试结果
• 1.字符文件
• 2.文本文件
• 3.图片文件
• 4.如果对压缩结果二次或者多次压缩，会不会每次都变小
• 5.Huffman压缩有无出现压缩结果变大的可能

前言

一、文件压缩

1.文件压缩的概念

文件压缩是指在不丢失有用信息的前提下，缩减数据量以减少存储空间，提高其传输、存储和处理效率，或按照一定的算法对文件中数据进行重新组织，减少数据的冗余和存储的空间的一种技术方法。

2.为什么需要压缩

①紧缩数据存储容量，减少存储空间。
②可以提高数据传输的速度，减少带宽占用量，提高通讯效率。
③对数据的一种加密保护，增强数据在传输过程中的安全性。

3.压缩的分类

• 有损压缩:有损压缩是利用了人类对图像或声波中的某些频率成分不敏感的特性，允许压缩过程中损失一定的信息；虽然不能完全恢复原始数据，但是所损失的部分对理解原始图像的影响缩小，却换来了大得多的压缩比，即指使用压缩后的数据进行重构，重构后的数据与原来的数据有所不同，但不影响人对原始资料表达的信息造成误解。
• 无损压缩:对文件中数据按照特定的编码格式进行重新组织，压缩后的压缩文件可以被还原成与源文件完全相同的格式，不会影响文件内容，对于数码图像而言，不会使图像细节有任何损失。

4.压缩的方法

压缩的目的是让文件变小，减少文件所占的存储空间。

专有名词采用的固定短语：比如：南昌大学，简称南大或者昌大，就可以提到压缩的目的，但只能针对于大家所熟知的专有名词。

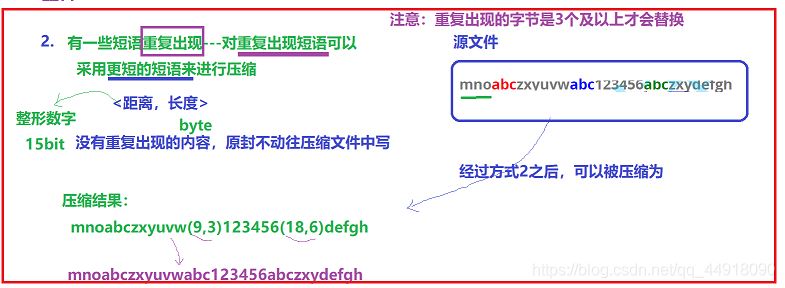
缩短文件中重复的数据：比如文件中存放数据为：mnoabczxyuvwabc123456abczxydefgh
对文件中重复数据使用(距离，长度)对进行替换，压缩之后的结果为：mnoabczxyuvw(9,3)123456(18, 6)defgh。

给文件中每个字节找一个更短的编码：比如文件中存放数据为：ABBBCCCCCDDDDDDD。

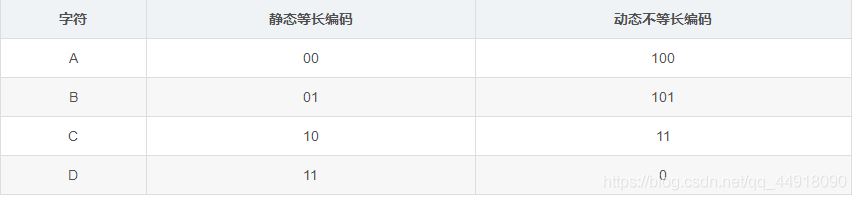
采用静态等长编码压缩： 00010101 10101010 10000000 00000000。

采用动态不等长编码压缩：10010110 11011111 11111100 00000000。

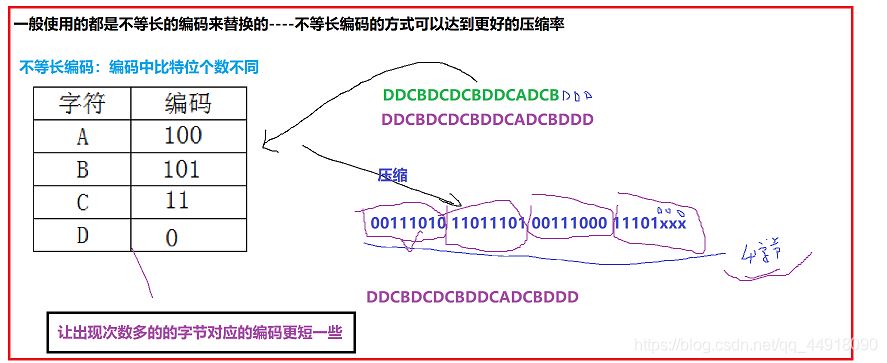
文件16个字节，压缩完成之后占4个字节，可以起到压缩的目的。

二、HuffmanTree文件压缩与解压缩

1.HuffmanTree的概念

在认识哈夫曼树之前，你必须知道以下几个基本术语：

①什么是路径？

在一棵树中，从一个结点往下可以达到的结点之间的通路，称为路径。

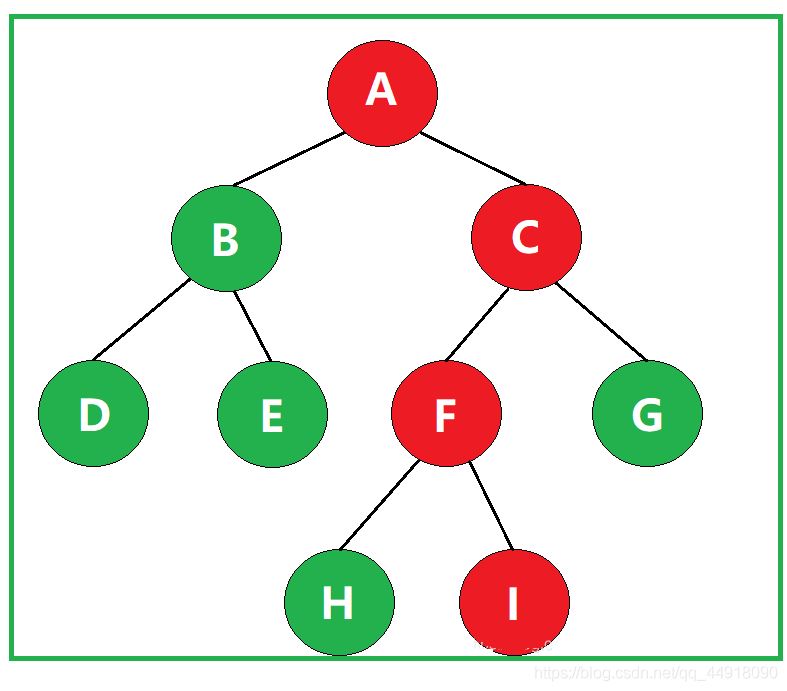
②什么是路径长度？

某一路径所经过的“边”的数量，称为该路径的路径长度。

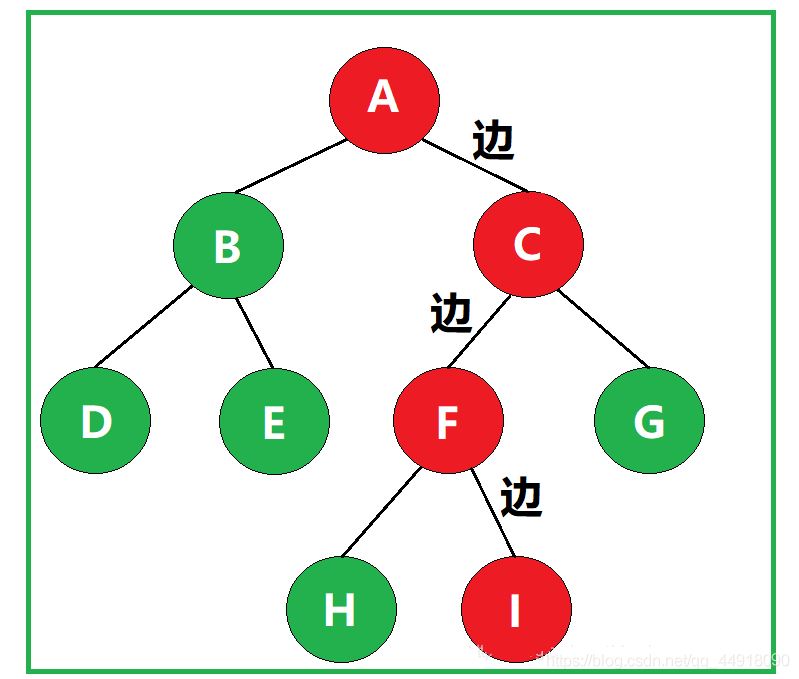
如图，该路径经过了3条边，因此该路径的路径长度为3。

③什么是结点的带权路径长度？

若将树中结点赋给一个带有某种含义的数值，则该数值称为该结点的权。从根结点到该结点之间的路径长度与该结点的权的乘积，称为该结点的带权路径长度。

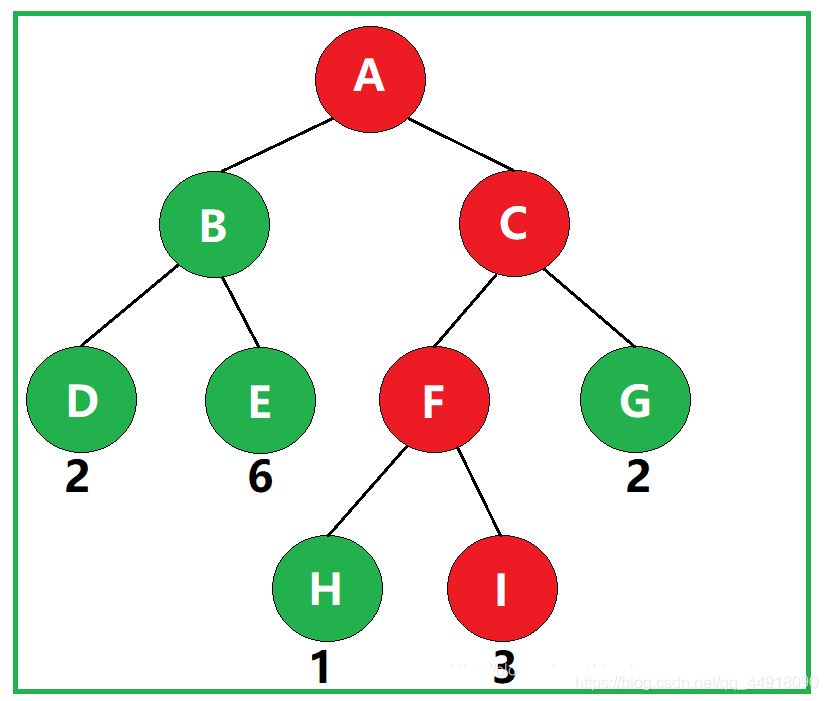
如图，叶子结点I的带权路径长度为 3 × 3 = 9 。

④什么是树的带权路径长度？

树的带权路径长度规定为所有叶子结点的带权路径长度之和，记为WPL。

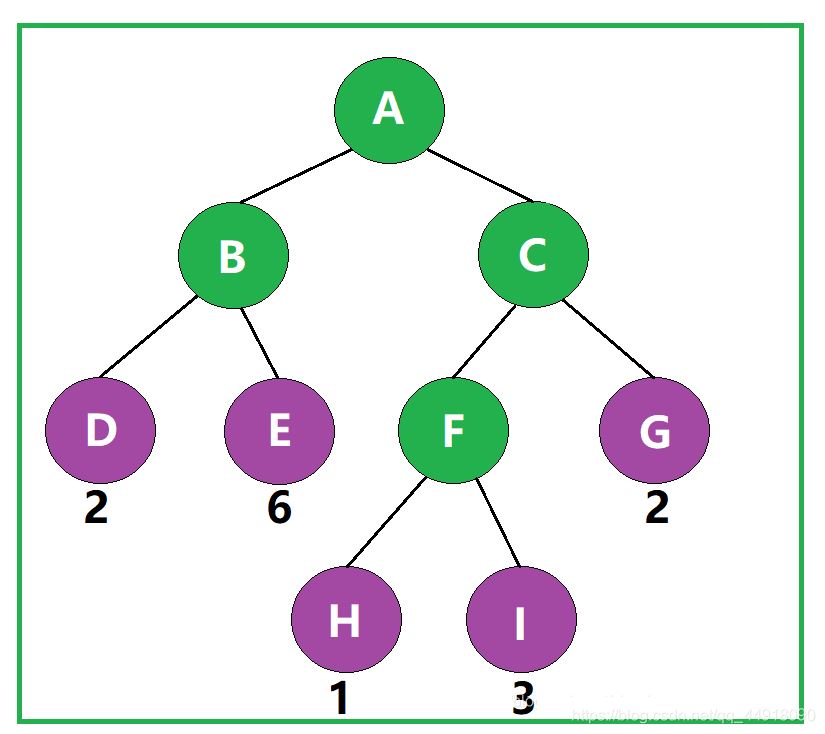
如图，该二叉树的带权路径长度 WPL= 2 × 2 + 2 × 6 + 3 × 1 + 3 × 3 + 2 × 2 = 32

⑤什么是哈夫曼树？

给定n个权值作为n个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，则称该二叉树为哈夫曼树，也被称为最优二叉树。

根据树的带权路径长度的计算规则，我们不难理解：树的带权路径长度与其叶子结点的分布有关。
即便是两棵结构相同的二叉树，也会因为其叶子结点的分布不同，而导致两棵二叉树的带权路径长度不同。

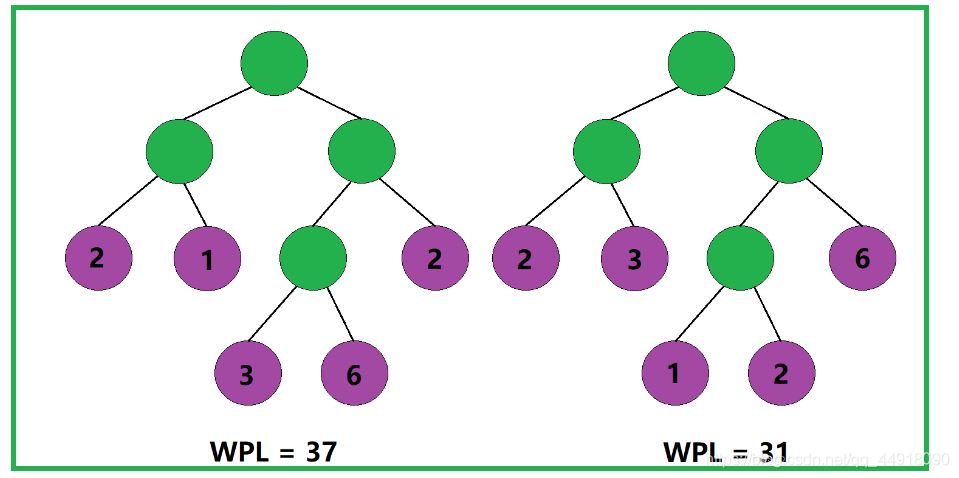
那如何才能使一棵二叉树的带权路径长度达到最小呢？
根据树的带权路径长度的计算规则，我们应该尽可能地让权值大的叶子结点靠近根结点，让权值小的叶子结点远离根结点，这样便能使得这棵二叉树的带权路径长度达到最小。

2.HuffmanTree的构建

下面给出一个非常简洁易操作的算法，来构造一棵哈夫曼树：
1、初始状态下共有n个结点，结点的权值分别是给定的n个数，将他们视作n棵只有根结点的树。
2、合并其中根结点权值最小的两棵树，生成这两棵树的父结点，权值为这两个根结点的权值之和，这样树的数量就减少了一个。
3、重复操作2，直到只剩下一棵树为止，这棵树就是哈夫曼树。

例如，现给定5个数，分别为1、2、2、3、6，要求构建一棵哈夫曼树。
动图演示：

1、初始状态：有5棵只有根结点的树。

2、合并权值为1和2的两棵树，生成这两棵树的父结点，父结点权值为3。

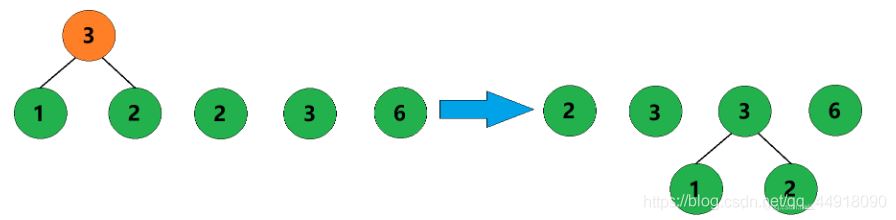
3、合并权值为2和3的两棵树，生成这两棵树的父结点，父结点权值为5。

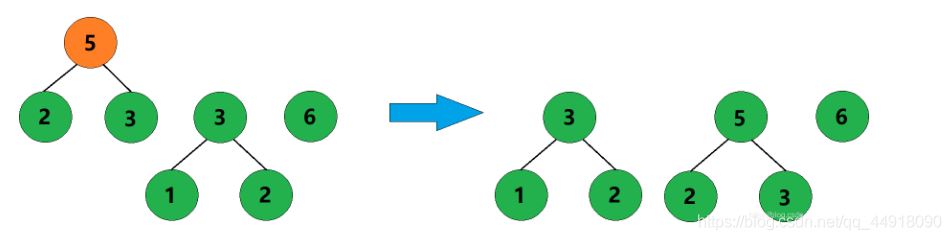
4、合并权值为3和5的两棵树，生成这两棵树的父结点，父结点权值为8。

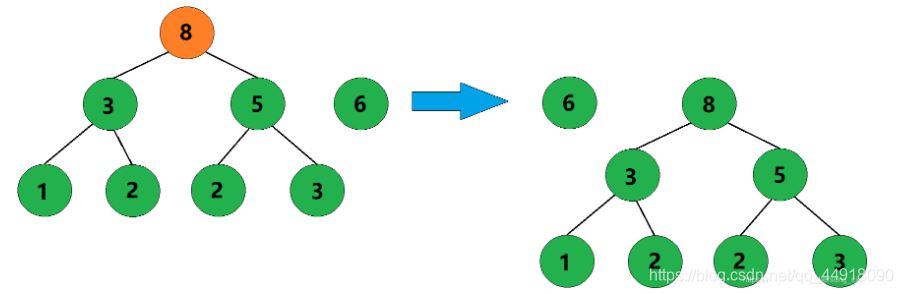
5、合并权值为6和8的两棵树，生成这两棵树的父结点，父结点权值为14。

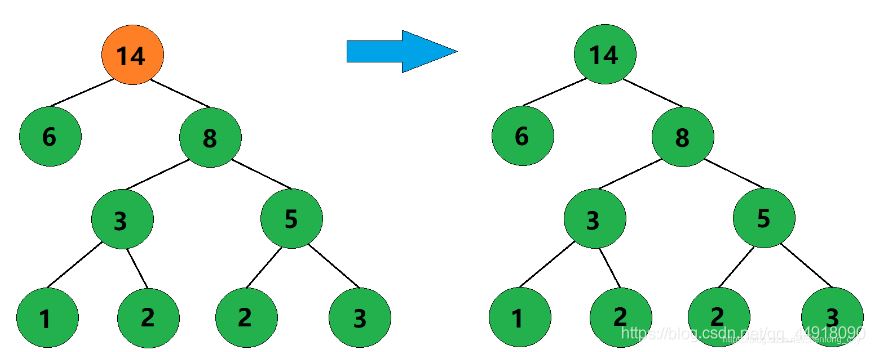
6、此时只剩下一棵树了，这棵树就是哈夫曼树。

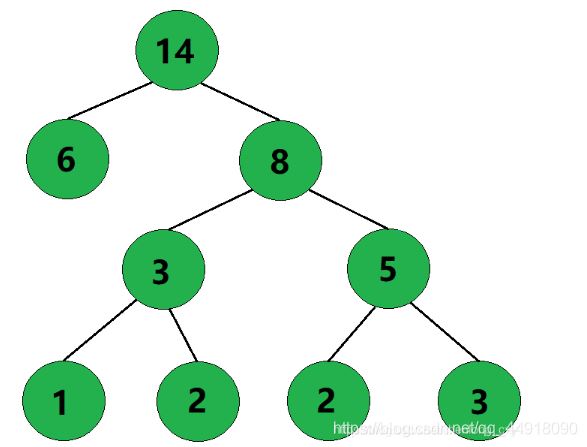
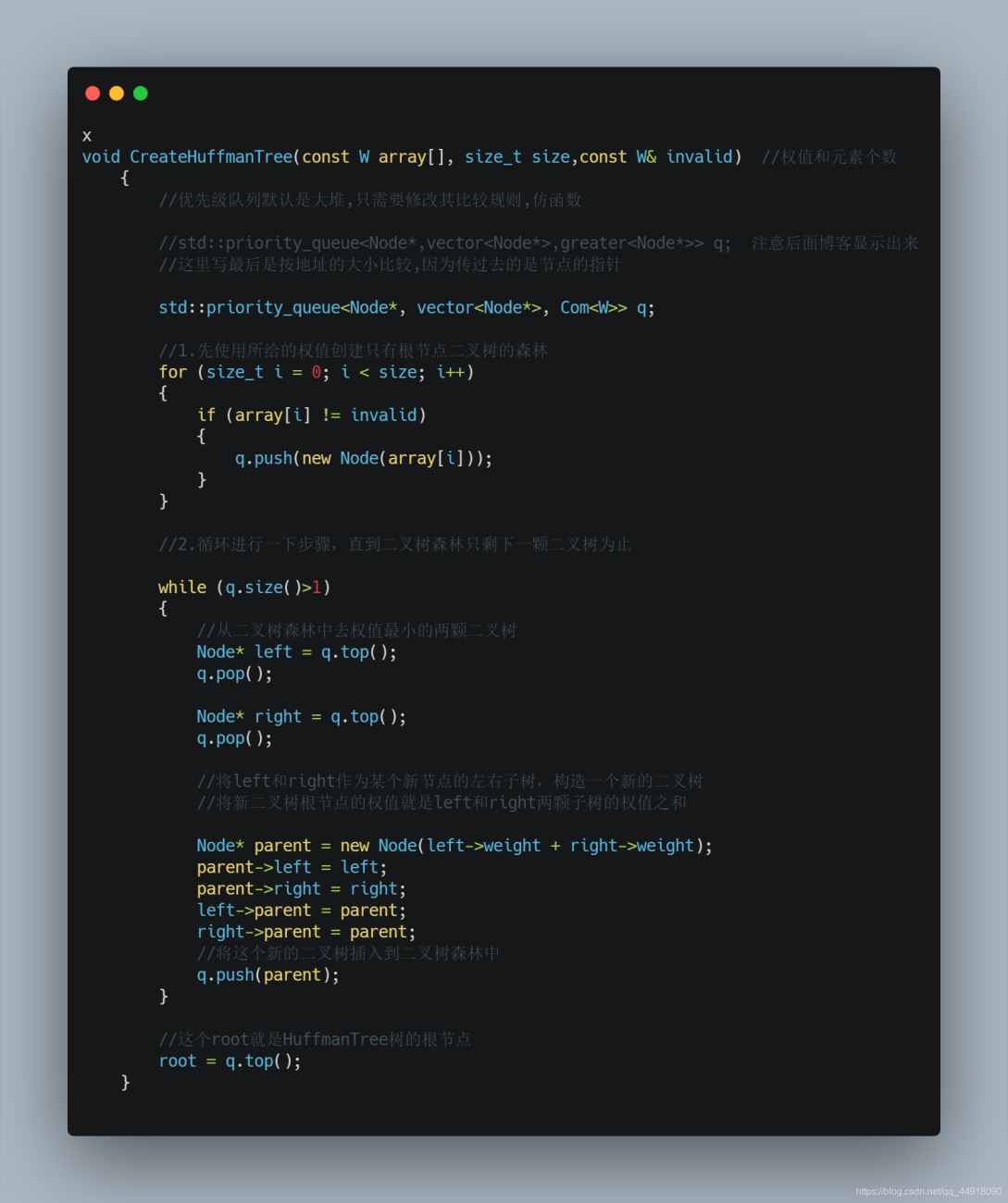
3.文件压缩

1.统计源文件中每个字符出现的频数

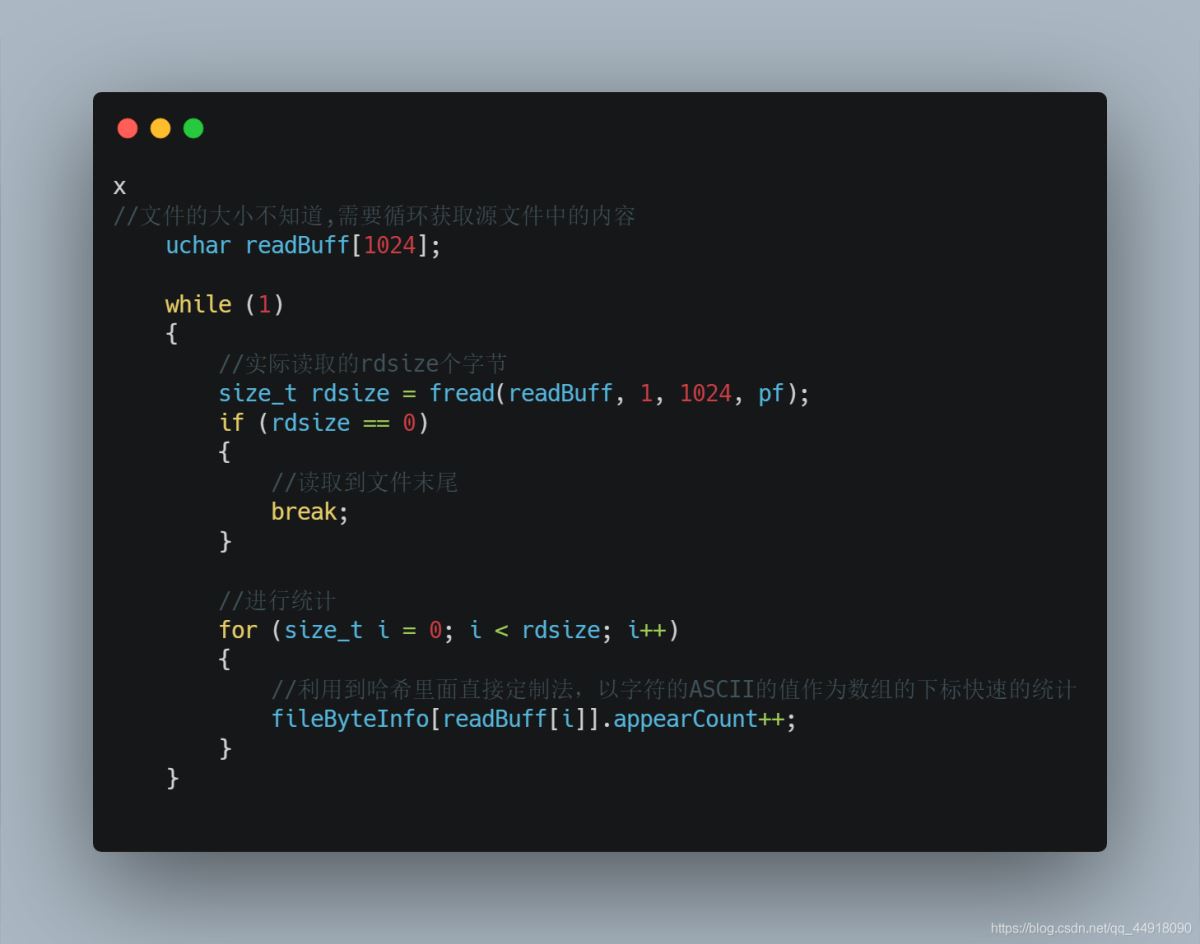
2.根据统计的结果创建HuffmanTree

3.借助Huffman树获取每个字节的编码

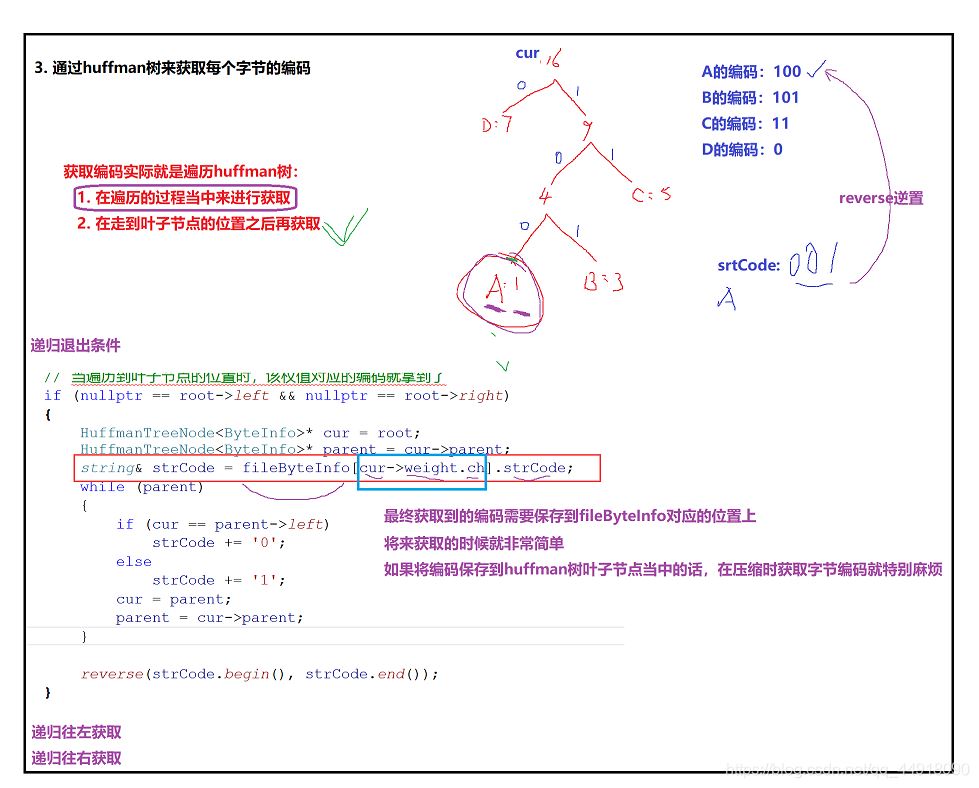
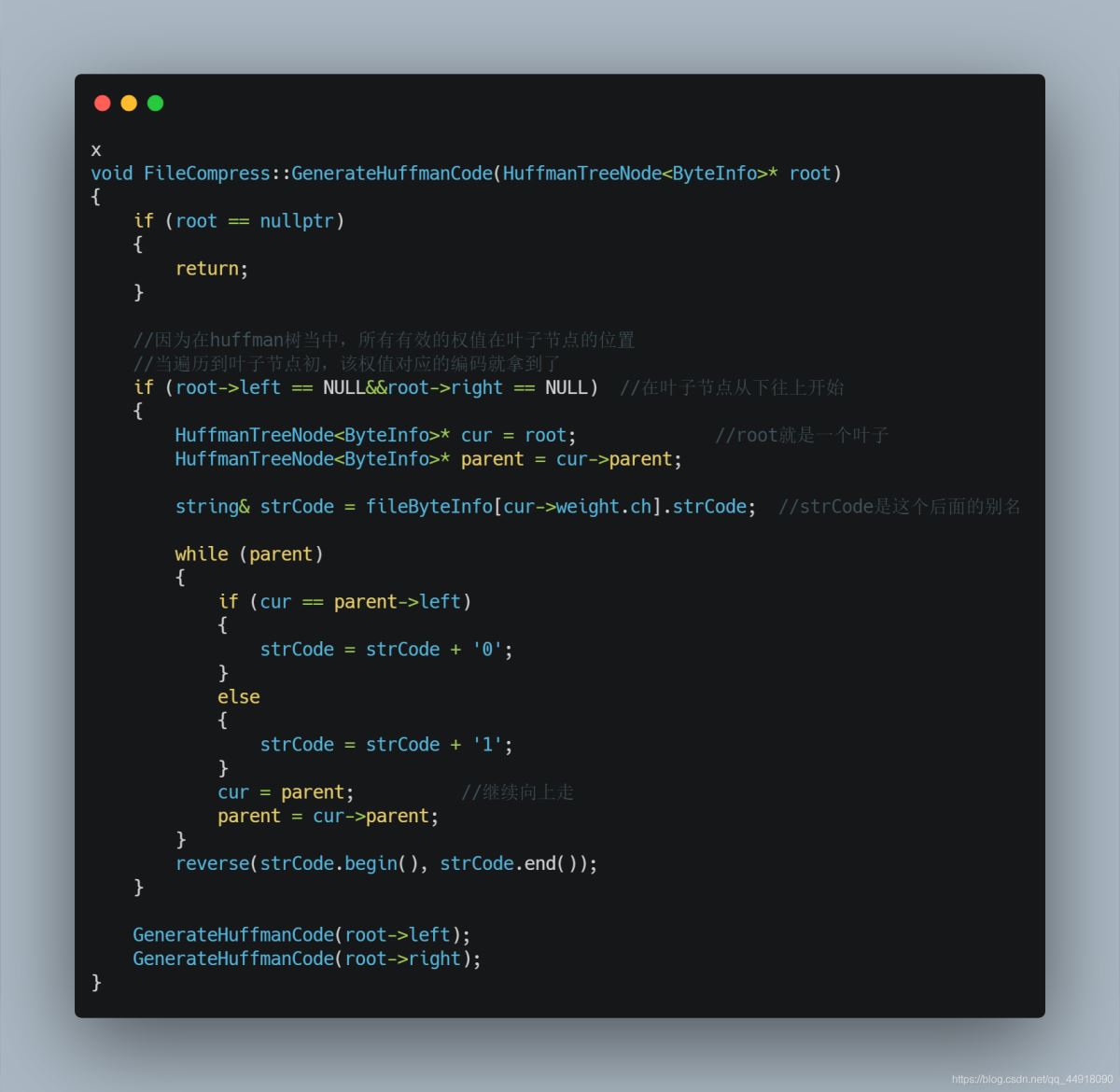
4.使用获取到的字节编码对源文件进行改写，对源文件每个字节替换成huffman编码

4.文件解压缩

1.解压缩需要获取的信息

1.获取源文件后缀
2.构建字节频次信息，统计有效字符总行数
3.写入信息

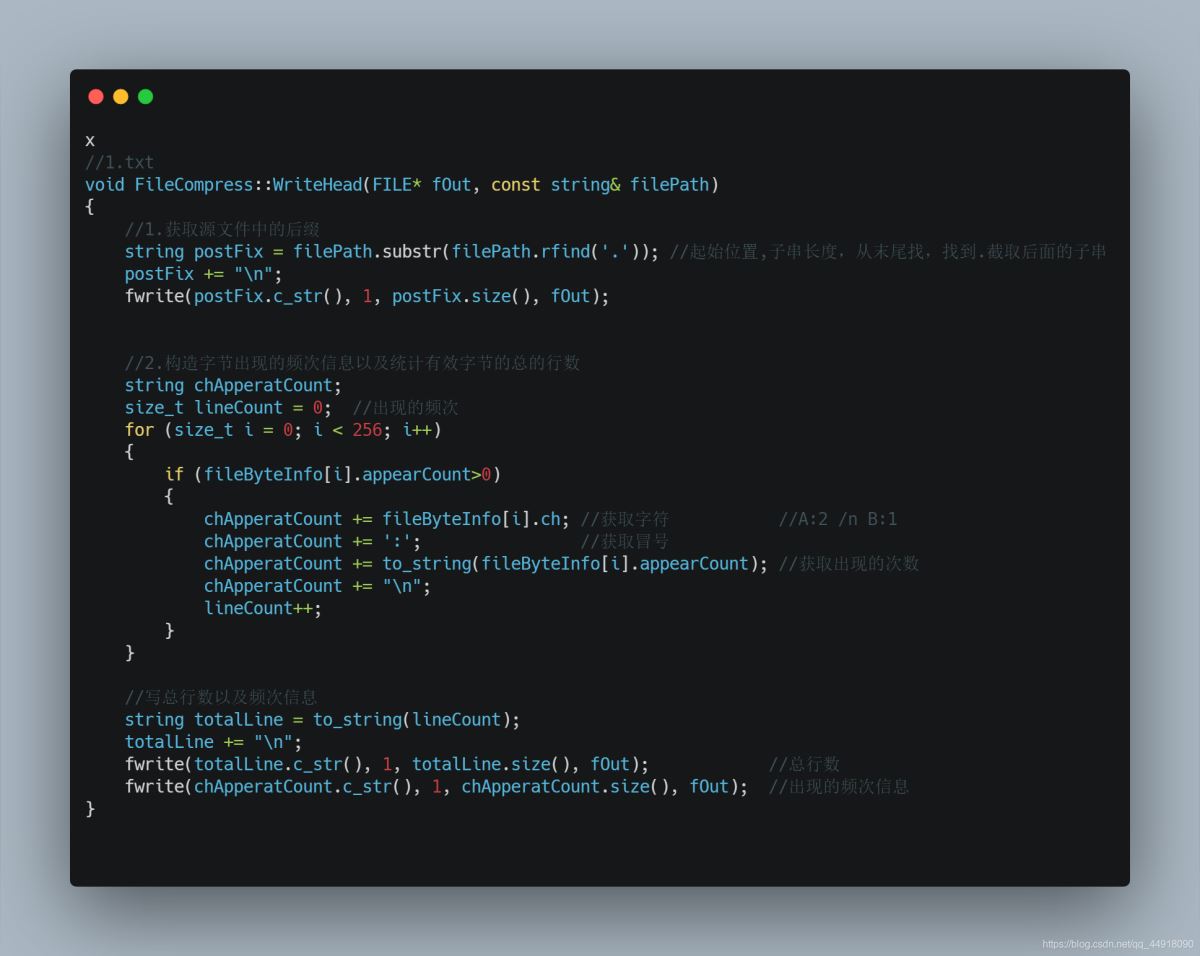
2.从压缩文件读取解压缩需要用到的信息

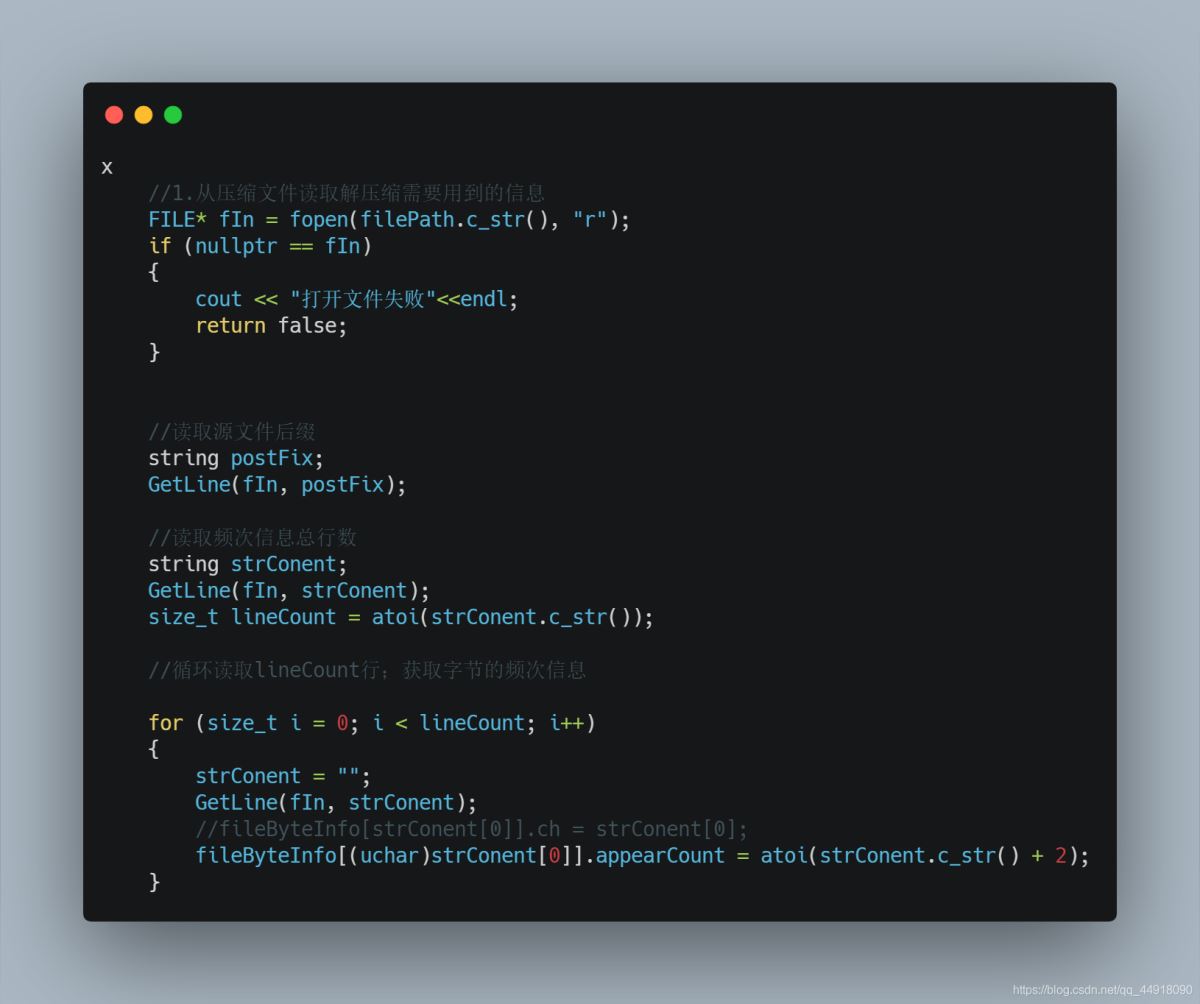
3.恢复huffmanTree

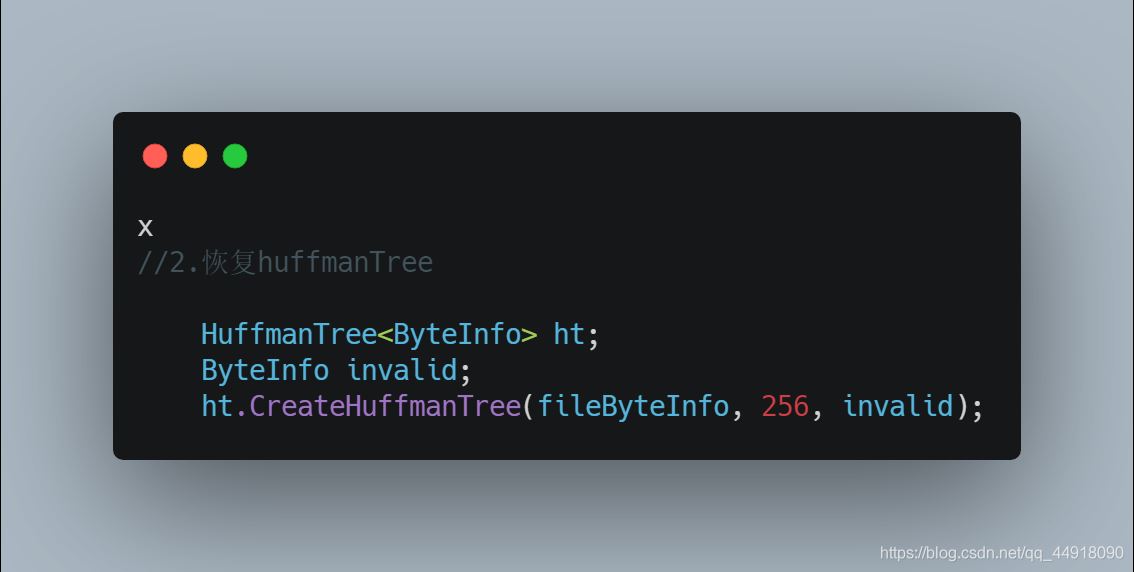
4.读取压缩信息,结合huffmanTree进行解压缩

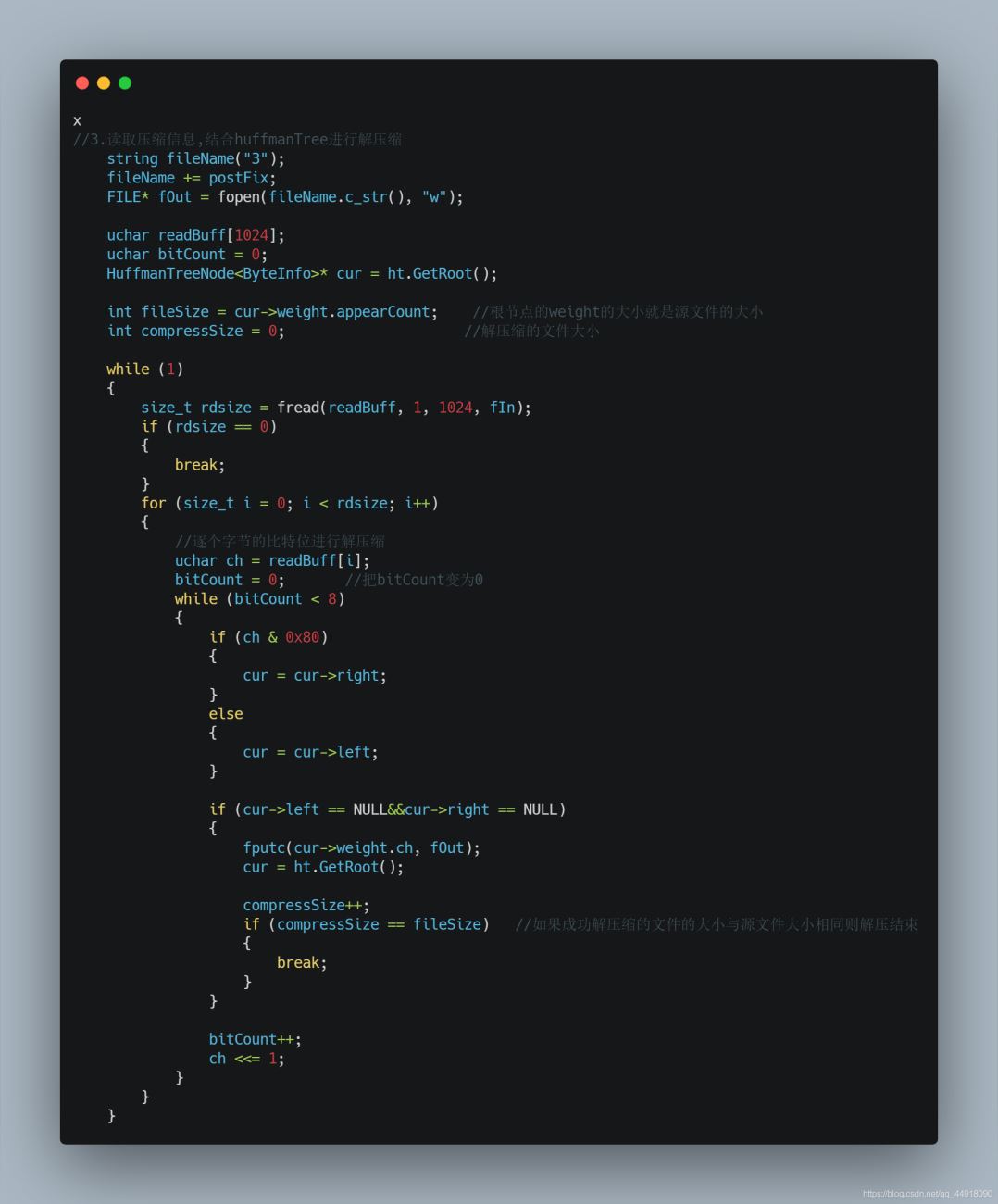
三、HuffmanTree压缩解压缩碰到的问题

1.创建优先级队列要使用自己写的仿函数

默认创建的是根据节点的地址来比较，这里写最后是按地址的大小比较,因为传过去的是节点的指针，而我们要根据根据节点里面的权值来创建小堆，所以自己写仿函数。

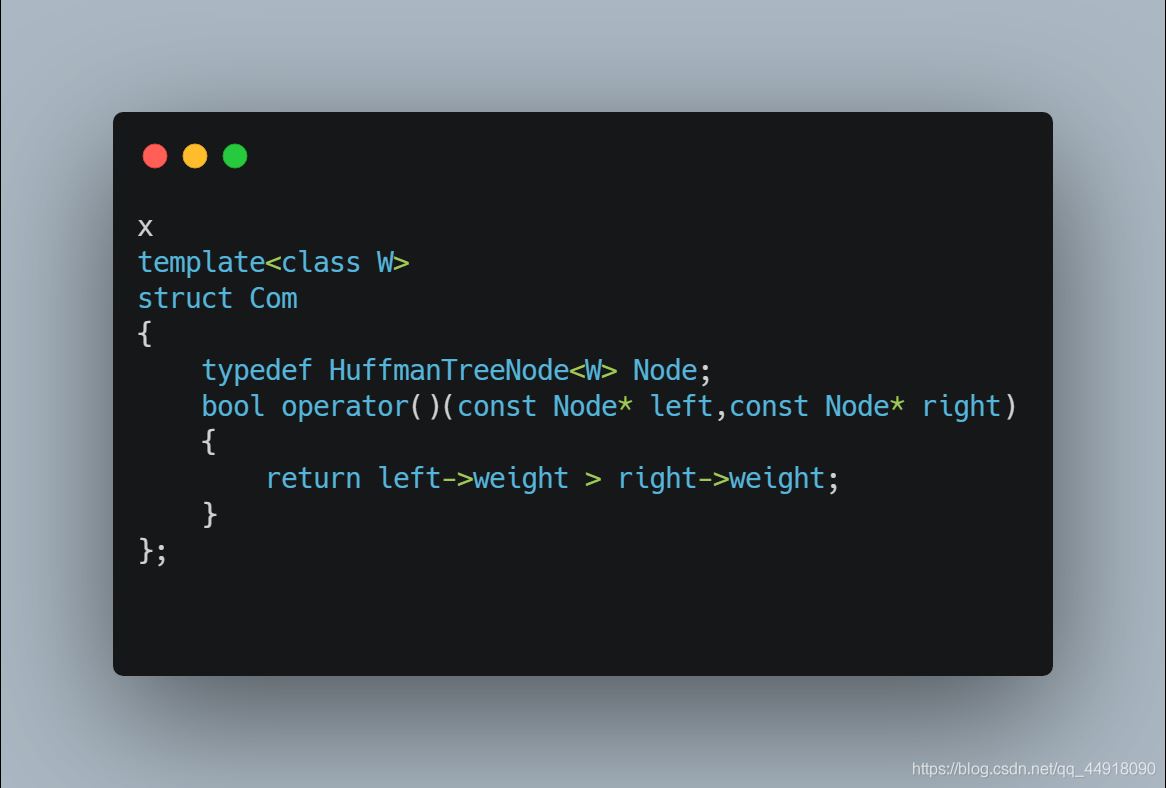
2.自定义类型结构体类型相加和仿函数要重载operator+和operator>

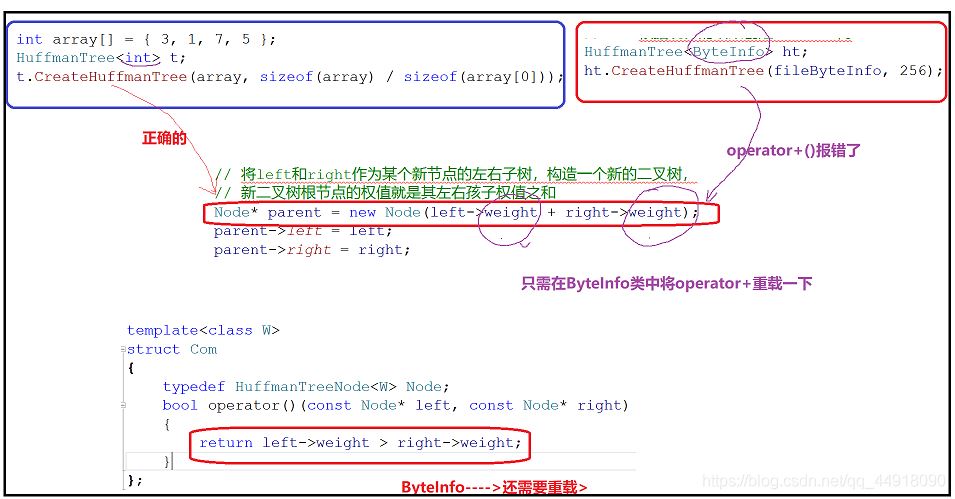
3.剔除在HuffmanTree出现0次的字符，不用统计出现0次的字符

4.如果在解压缩时，最后一个字节的压缩数据不满8个比特位，则在解压缩过程中如何处理？

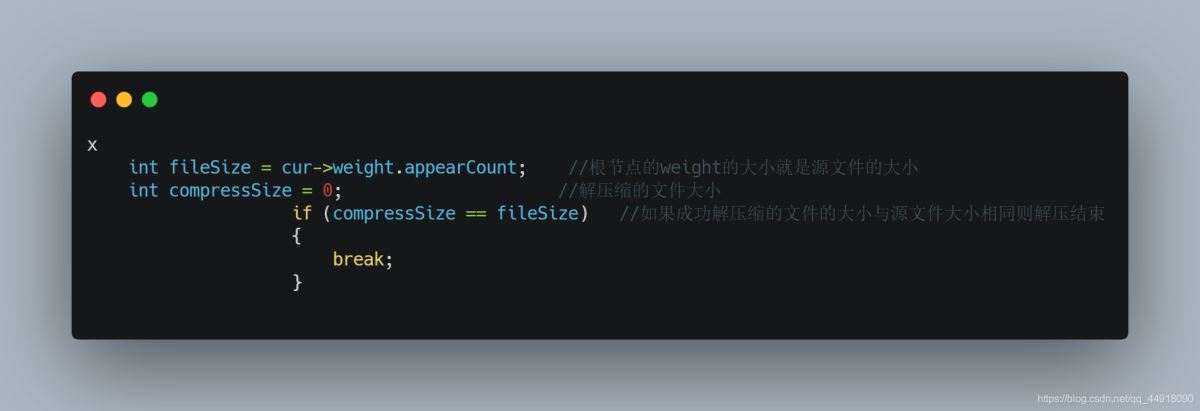
5.在解压缩源文件中有汉字，解压缩过时出现乱码，怎么处理？

首先应该注意到是的乱码出现的原因：
1.文件中存在汉字，而汉字的编码对应ASCII表可能是使用多个字节来编码一个汉字，但是在解码过程中是逐字节获取，这就导致了该字节在表中对应一个负数。

压缩带中文的文件，程序就会崩溃。

最后发现数组越界的问题.
因为char它的范围是-128127，程序中使用char类型为数组下标（0127），所以字符没有问题，但是汉字是占两个字节的，所以会出现越界的问题，解决的方法就是char类型强转为unsigned char，它的范围为0~255。

6.文件中包含多行文本时解压缩出现乱码

最直接的排错方式：查看压缩与解压缩时使用的Huffman树是否相同，相当于比较压缩与解压缩时所使用的字节频次信息是否相同，遇到换行时，直接开始下一次循环，以至于最后的循环少一次。

7.解压缩文件大小小于源文件大小，没有解压缩全部如何解决

①如何判断解压缩文件是否正确，使用的是Ultar Edit

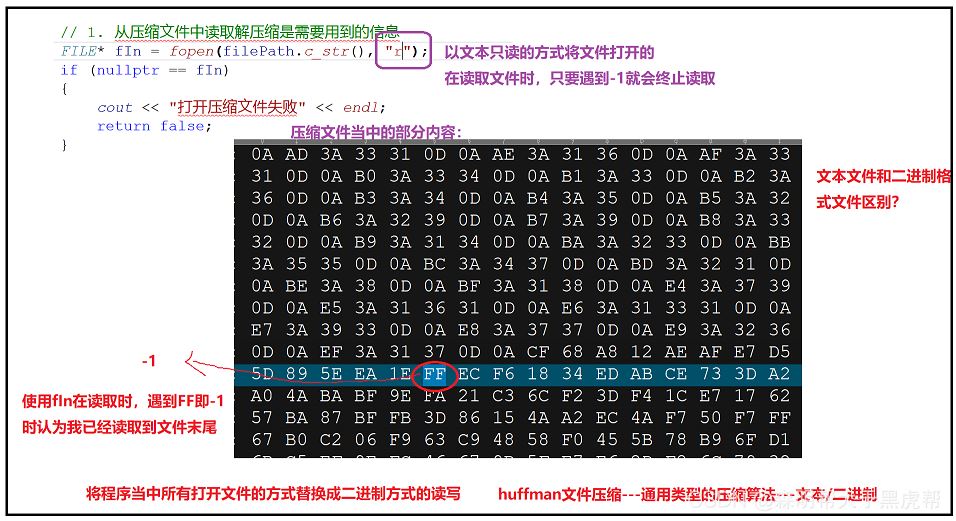
②文件读取时，”r"文本方式读入，读取时遇到-1就会结束，所以在此处要采用二进制方式进行读写“rb”

四、测试结果

1.字符文件

自带的压缩软件为1KB,这个为6KB。

2.文本文件

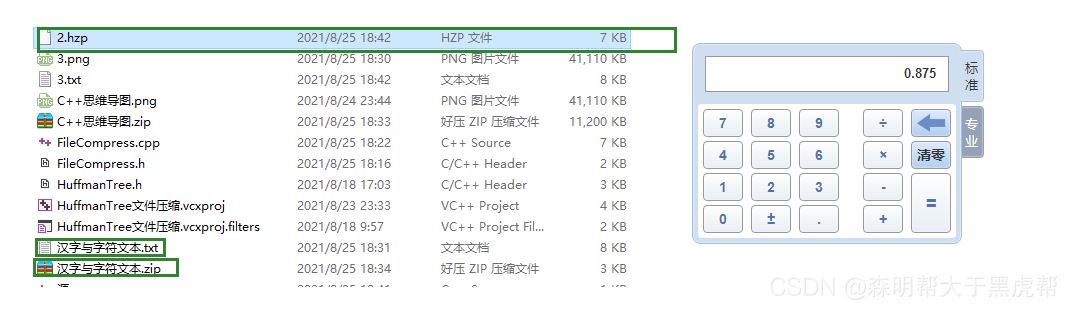
3.图片文件

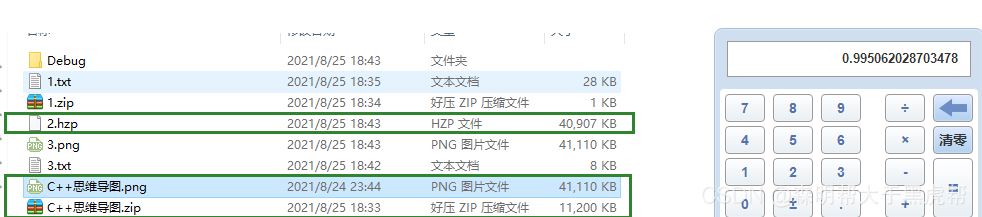
4.如果对压缩结果二次或者多次压缩，会不会每次都变小

不会，对压缩文件再次压缩就相当于在进行一次Huffman编码的基础上再进行编码，结果不一定。

5.Huffman压缩有无出现压缩结果变大的可能

有，在文件中如果字节的种类非常多，而且出现次数比较均衡的情况下，变大的可能性就越大，Huffman树在越接近平衡二叉树的情况下，压缩结果越不理想，字节的编码长度都差不多，比如压缩音频以及视频文件，压缩率都超过了100%！

6.结论

文本文件的压缩率比二进制文件的压缩率更好，因为文本文件的编码相比于二进制文件的编码相对更简单，导致了文件压缩率的差距较大。相比传统的压缩工具，这个工具压缩效率基本为传统压缩效率的3分之一。

到此这篇关于C++项目基于HuffmanTree实现文件的压缩与解压缩功能的文章就介绍到这了,更多相关C++文件的压缩与解压缩内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！