Python技法之简单递归下降Parser的实现方法

目录

• 1. 算术运算表达式求值
• 2. 生成表达式树
• 左递归和运算符优先级陷阱
• 3. 相关包
• 参考
• 总结

1. 算术运算表达式求值

在上一篇博文《Python技法：用re模块实现简易tokenizer》中，我们介绍了用正则表达式来匹配对应的模式，以实现简单的分词器。然而，正则表达式不是万能的，它本质上是一种有限状态机（finite state machine，FSM）, 无法处理含有递归语法的文本，比如算术运算表达式。

要解析这类文本，需要另外一种特定的语法规则。我们这里介绍可以表示上下文无关文法（context free grammer）的语法规则巴科斯范式(BNF)和扩展巴科斯范式(EBNF)。实际上，小到一个算术运算表达式，大到几乎所有程序设计语言，都是通过上下文无关文法来定义的。

对于简单的算术运算表达式，假定我们已经用分词技术将其转化为输入的tokens流，如NUM+NUM*NUM（分词方法参见上一篇博文）。

在此基础上，我们定义BNF规则定义如下：

expr ::= expr + term
     | expr - term
     | term
term ::= term * factor
     | term / factor
     | factor
factor ::= (expr)
     | NUM

当然，这种计法还不够简洁明了，我们实际采用的为EBNF形式：

expr ::= term { (+|-) term }*
term ::= factor { (*|/) factor }*
factor ::= (expr)
       | NUM

BNF和EBNF每一条规则(形如::=的式子)都可以看做是一种替换，即左侧的符号可以被右侧的符号所替换。而解析的过程中我们尝试将输入文本同语法规则做匹配，通过BNF/EBNF来完成各种替换和扩展。其中，EBNF中包含在{...}*中的规则是可选的，*意味着零个或多个重复项（参考正则表达式）。

下图形象地展示了递归下降解析器(parser)中“递归”和“下降”部分和ENBF的关系：

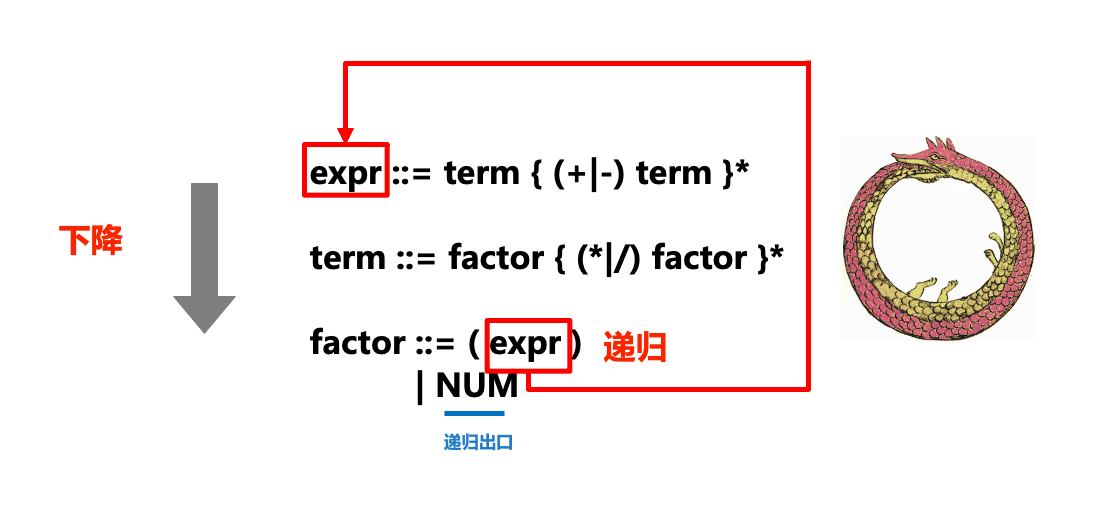
在实际的解析过程中，我们对tokens流从左到右进行扫描，在扫描的过程中处理token，如果卡住就产生一个语法错误。对于规则，我们将每一条语法规则转变为一个函数或方法，比如上面的ENBF规则就转换为下列的方法：

class ExpressionEvaluator():
    ...
    def expr(self):
        ...
    def term(self):
        ...
    def factor(self):
        ...

在调用某个规则对应方法的过程中，如果我们发现接下来的符号需要采用另一个规则来匹配，则我们就会“下降”到另一个规则方法（如在expr中调用term，term中调用factor），则也就是递归下降中“下降”的部分。

有时也会调用已经在执行的方法（比如在expr中调用term，term中调用factor后，又在factor中调用expr，相当于一条衔尾蛇），这也就是递归下降中“递归”的部分。

对于语法中出现的重复部分（例如expr ::= term { (+|-) term }*），我们则通过while循环来实现。

下面我们来看具体的代码实现。首先是分词部分，我们参照上一篇介绍分词博客的代码。

import re
import collections

# 定义匹配token的模式
NUM = r'(?P<NUM>\d+)'  # \d表示匹配数字，+表示任意长度
PLUS = r'(?P<PLUS>\+)'  # 注意转义
MINUS = r'(?P<MINUS>-)'
TIMES = r'(?P<TIMES>\*)'  # 注意转义
DIVIDE = r'(?P<DIVIDE>/)'
LPAREN = r'(?P<LPAREN>\()'  # 注意转义
RPAREN = r'(?P<RPAREN>\))'  # 注意转义
WS = r'(?P<WS>\s+)'  # 别忘记空格，\s表示空格，+表示任意长度

master_pat = re.compile(
    '|'.join([NUM, PLUS, MINUS, TIMES, DIVIDE, LPAREN, RPAREN, WS]))

# Tokenizer
Token = collections.namedtuple('Token', ['type', 'value'])

def generate_tokens(text):
    scanner = master_pat.scanner(text)
    for m in iter(scanner.match, None):
        tok = Token(m.lastgroup, m.group())
        if tok.type != 'WS':  # 过滤掉空格符
            yield tok

下面是表达式求值器的具体实现：

class ExpressionEvaluator():
    """ 递归下降的Parser实现，每个语法规则都对应一个方法，
    使用 ._accept()方法来测试并接受当前处理的token，不匹配不报错，
    使用 ._except()方法来测试当前处理的token，并在不匹配的时候抛出语法错误
    """

    def parse(self, text):
        """ 对外调用的接口 """
        self.tokens = generate_tokens(text)
        self.tok, self.next_tok = None, None  # 已匹配的最后一个token，下一个即将匹配的token
        self._next()  # 转到下一个token
        return self.expr()  # 开始递归

    def _next(self):
        """ 转到下一个token """
        self.tok, self.next_tok = self.next_tok, next(self.tokens, None)

    def _accept(self, tok_type):
        """ 如果下一个token与tok_type匹配，则转到下一个token """
        if self.next_tok and self.next_tok.type == tok_type:
            self._next()
            return True
        else:
            return False

    def _except(self, tok_type):
        """ 检查是否匹配，如果不匹配则抛出异常 """
        if not self._accept(tok_type):
            raise SyntaxError("Excepted"+tok_type)

    # 接下来是语法规则，每个语法规则对应一个方法

    def expr(self):
        """ 对应规则： expression ::= term { ('+'|'-') term }* """
        exprval = self.term() # 取第一项
        while self._accept("PLUS") or self._accept("DIVIDE"): # 如果下一项是"+"或"-"
            op = self.tok.type
            # 再取下一项，即运算符右值
            right = self.term()
            if op == "PLUS":
                exprval += right
            elif op == "MINUS":
                exprval -= right
        return exprval

    def term(self):
        """ 对应规则： term ::= factor { ('*'|'/') factor }* """

        termval = self.factor() # 取第一项
        while self._accept("TIMES") or self._accept("DIVIDE"): # 如果下一项是"+"或"-"
            op = self.tok.type
            # 再取下一项，即运算符右值
            right = self.factor()
            if op == "TIMES":
                termval *= right
            elif op == "DIVIDE":
                termval /= right
        return termval          

    def factor(self):
        """ 对应规则： factor ::= NUM | ( expr ) """
        if self._accept("NUM"): # 递归出口
            return int(self.tok.value)
        elif self._accept("LPAREN"):
            exprval = self.expr() # 继续递归下去求表达式值
            self._except("RPAREN") # 别忘记检查是否有右括号，没有则抛出异常
            return exprval
        else:
            raise SyntaxError("Expected NUMBER or LPAREN")

我们输入以下表达式进行测试：

e = ExpressionEvaluator()
print(e.parse("2"))
print(e.parse("2+3"))
print(e.parse("2+3*4"))
print(e.parse("2+(3+4)*5"))

求值结果如下：

2
5
14
37

如果我们输入的文本不符合语法规则：

print(e.parse("2 + (3 + * 4)"))

则会抛出SyntaxError异常：Expected NUMBER or LPAREN。
综上，可见我们的表达式求值算法运行正确。

2. 生成表达式树

上面我们是得到表达式的结果，但是如果我们想分析表达式的结构，生成一棵简单的表达式解析树呢？那么我们需要对上述类的方法做一定修改：

class ExpressionTreeBuilder(ExpressionEvaluator):
    def expr(self):
            """ 对应规则： expression ::= term { ('+'|'-') term }* """
            exprval = self.term() # 取第一项
            while self._accept("PLUS") or self._accept("DIVIDE"): # 如果下一项是"+"或"-"
                op = self.tok.type
                # 再取下一项，即运算符右值
                right = self.term()
                if op == "PLUS":
                    exprval = ('+', exprval, right)
                elif op == "MINUS":
                    exprval -= ('-', exprval, right)
            return exprval

    def term(self):
        """ 对应规则： term ::= factor { ('*'|'/') factor }* """

        termval = self.factor() # 取第一项
        while self._accept("TIMES") or self._accept("DIVIDE"): # 如果下一项是"+"或"-"
            op = self.tok.type
            # 再取下一项，即运算符右值
            right = self.factor()
            if op == "TIMES":
                termval = ('*', termval, right)
            elif op == "DIVIDE":
                termval = ('/', termval, right)
        return termval          

    def factor(self):
        """ 对应规则： factor ::= NUM | ( expr ) """
        if self._accept("NUM"): # 递归出口
            return int(self.tok.value) # 字符串转整形
        elif self._accept("LPAREN"):
            exprval = self.expr() # 继续递归下去求表达式值
            self._except("RPAREN") # 别忘记检查是否有右括号，没有则抛出异常
            return exprval
        else:
            raise SyntaxError("Expected NUMBER or LPAREN")

输入下列表达式测试一下：

print(e.parse("2+3"))
print(e.parse("2+3*4"))
print(e.parse("2+(3+4)*5"))
print(e.parse('2+3+4'))

以下是生成结果：

('+', 2, 3)
('+', 2, ('*', 3, 4))
('+', 2, ('*', ('+', 3, 4), 5))
('+', ('+', 2, 3), 4)

可以看到表达式树生成正确。

我们上面的这个例子非常简单，但递归下降的解析器也可以用来实现相当复杂的解析器，例如Python代码就是通过一个递归下降解析器解析的。您要是对此跟感兴趣可以检查Python源码中的Grammar文件来一探究竟。然而，下面我们接着会看到，自己动手写一个解析器会面对各种陷阱和挑战。

左递归和运算符优先级陷阱

任何涉及左递归形式的语法规则，都没法用递归下降parser来解决。所谓左递归，即规则式子右侧最左边的符号是规则头，比如对于以下规则：

items ::= items ',' item
      | item

完成该解析你可能会定义以下方法：

def items(self):
    itemsval = self.items() # 取第一项，然而此处会无穷递归！
    if itemsval and self._accept(','):
        itemsval.append(self.item())
    else:
        itemsval = [self.item()]

这样做会在第一行就无穷地调用self.items()从而产生无穷递归错误。

还有一种是语法规则自身的错误，比如运算符优先级。我们如果忽视运算符优先级直接将表达式简化如下：

expr ::= factor { ('+'|'-'|'*'|'/') factor }*
factor ::= '(' expr ')'
       | NUM

PYTHON 复制 全屏

这个语法从技术上可以实现，但是没有遵守计算顺序约定，导致"3+4*5"的运算结果为35，而不是预期的23。故此处需要用独立的expr和term规则来确保计算结果的正确性。

3. 相关包

最后，对于真正复杂的语法解析，建议采用PyParsing或PLY这样的解析工具。如果你对Python代码的抽象语法树感兴趣，可以看下Python自带的ast模块。

参考

• [1] Martelli A, Ravenscroft A, Ascher D. Python cookbook[M]. " O'Reilly Media, Inc.", 2015.
• [2] https://cs61a.org/study-guide/regex/
• [3] https://cs61a.org/study-guide/bnf/
• [4] https://zh.wikipedia.org/wiki/巴科斯范式

总结

到此这篇关于Python技法之简单递归下降Parser实现的文章就介绍到这了,更多相关Python递归下降Parser内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！