浅谈Python描述数据结构之KMP篇
前言
本篇章主要介绍串的KMP模式匹配算法及其改进,并用Python实现KMP算法。
1. BF算法
BF算法,即Bruce−ForceBruce-ForceBruce−Force算法,又称暴力匹配算法。其思想就是将主串S的第一个字符与模式串T的第一个字符进行匹配,若相等,则继续比较S的第二个字符和T的第二个字符;若不相等,则比较S的第二个字符和T的第一个字符,依次比较下去,直到得出最后的匹配结果。
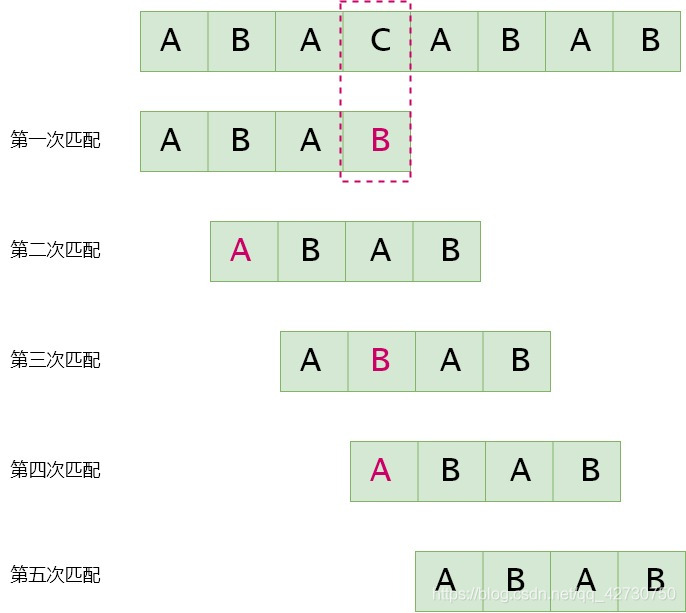
假设主串S=ABACABABS=ABACABABS=ABACABAB,模式串T=ABABT=ABABT=ABAB,每趟匹配失败后,主串S指针回溯,模式串指针回到头部,然后再次匹配,过程如下:
def BF(substrS, substrT):
if len(substrT) > len(substrS):
return -1
j = 0
t = 0
while j < len(substrS) and t < len(substrT):
if substrT[t] == substrS[j]:
j += 1
t += 1
else:
j = j - t + 1
t = 0
if t == len(substrT):
return j - t
else:
return -1
2. KMP算法
KMP算法,是由D.E.Knuth、J.H.Morris、V.R.PrattD.E.Knuth、J.H.Morris、V.R.PrattD.E.Knuth、J.H.Morris、V.R.Pratt同时发现的,又被称为克努特-莫里斯-普拉特算法。该算法的基本思路就是在匹配失败后,无需回到主串和模式串最近一次开始比较的位置,而是在不改变主串已经匹配到的位置的前提下,根据已经匹配的部分字符,从模式串的某一位置开始继续进行串的模式匹配。
就是这次匹配失败时,下次匹配时模式串应该从哪一位开始比较。
BF算法思路简单,便于理解,但是在执行时效率太低。在上述的匹配过程中,第一次匹配时已经匹配的"ABA""ABA""ABA",其前缀与后缀都是"A""A""A",这个时候我们就不需要执行第二次匹配了,因为第一次就已经匹配过了,所以可以跳过第二次匹配,直接进行第三次匹配,即前缀位置移到后缀位置,主串指针无需回溯,并继续从该位开始比较。
前缀:是指除最后一个字符外,字符串的所有头部子串。
后缀:是指除第一个字符外,字符串的所有尾部子串。
部分匹配值(Partial(Partial(Partial Match,PM)Match,PM)Match,PM):字符串的前缀和后缀的最长相等前后缀长度。
例如,′a′'a'′a′的前缀和后缀都为空集,则最长公共前后缀长度为0;′ab′'ab'′ab′的前缀为{a}\{a\}{a},后缀为{b}\{b\}{b},则最长公共前后缀为空集,其长度长度为0;′aba′'aba'′aba′的前缀为{a,ab}\{a,ab\}{a,ab},后缀为{a,ba}\{a,ba\}{a,ba},则最长公共前后缀为{a}\{a\}{a},其长度长度为1;′abab′'abab'′abab′的前缀为{a,ab,aba}\{a,ab,aba\}{a,ab,aba},后缀为{b,ab,bab}\{b,ab,bab\}{b,ab,bab},则最长公共前后缀为{ab}\{ab\}{ab},其长度长度为2。
前缀一定包含第一个字符,后缀一定包含最后一个字符。
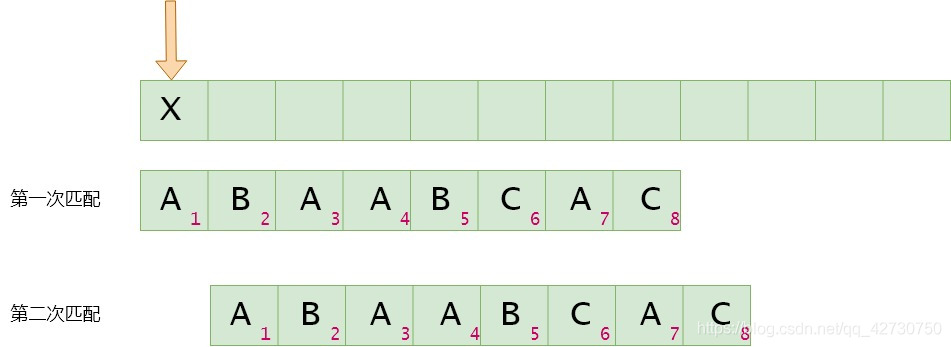
如果模式串1号位与主串当前位(箭头所指的位置)不匹配,将模式串1号位与主串的下一位进行比较。next[0]=-1,这边就是一个特殊位置了,即如果主串与模式串的第1位不相同,那么下次就直接比较各第2位的字符。
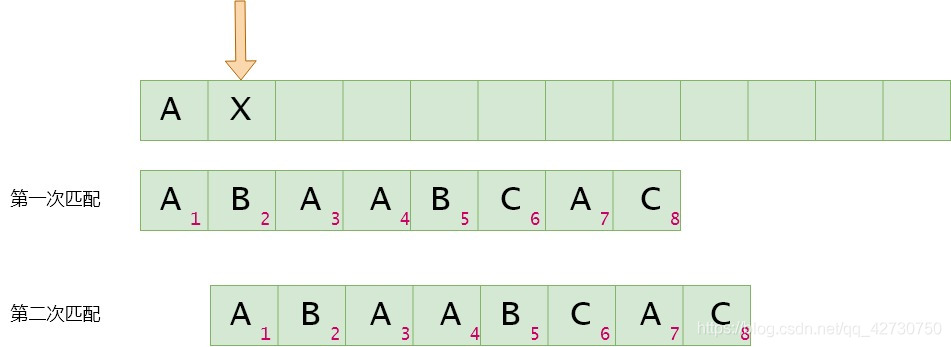
如果模式串2号位与主串当前位不匹配,找最长公共前后缀,指针前面的子串为"A""A""A",即最长公共前后缀为空集,其长度为0,则下次匹配时将模式串1号位与主串的当前位进行比较。next[1]=0
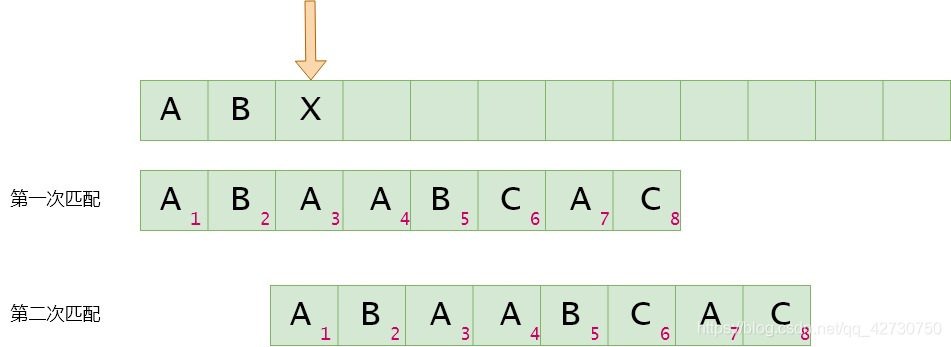
如果模式串3号位与主串当前位不匹配,找最长公共前后缀,指针前面的子串为"AB""AB""AB",即最长公共前后缀为空集,其长度为0,则下次匹配时将模式串1号位与主串的当前位进行比较。next[2]=0
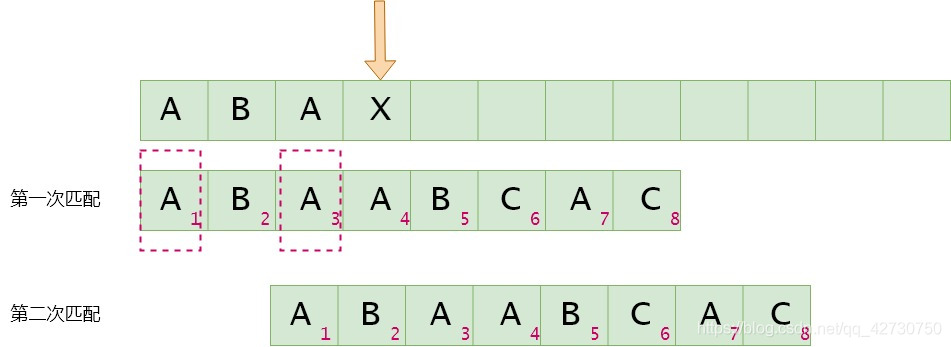
如果模式串4号位与主串当前位不匹配,找最长公共前后缀,指针前面的子串为"ABA""ABA""ABA",即最长公共前后缀为"A""A""A",其长度为1,则下次匹配时将前缀位置移到后缀位置,即模式串2号位与主串的当前位进行比较。next[3]=1
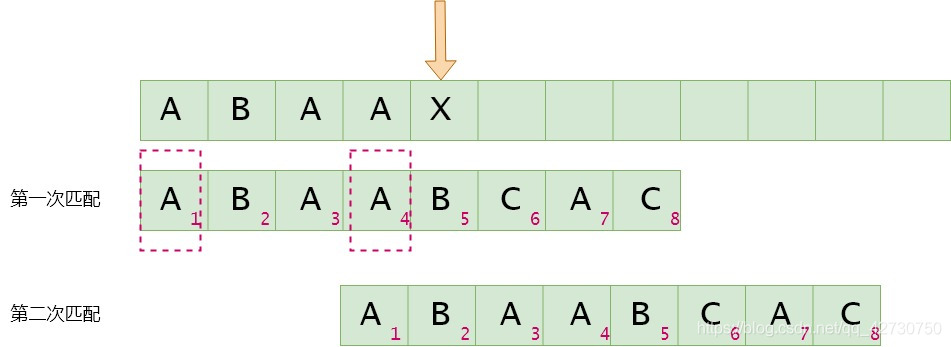
如果模式串5号位与主串当前位不匹配,找最长公共前后缀,指针前面的子串为"ABAA""ABAA""ABAA",即最长公共前后缀为"A""A""A",其长度为1,则下次匹配时将前缀位置移到后缀位置,即模式串2号位与主串的当前位进行比较。next[4]=1
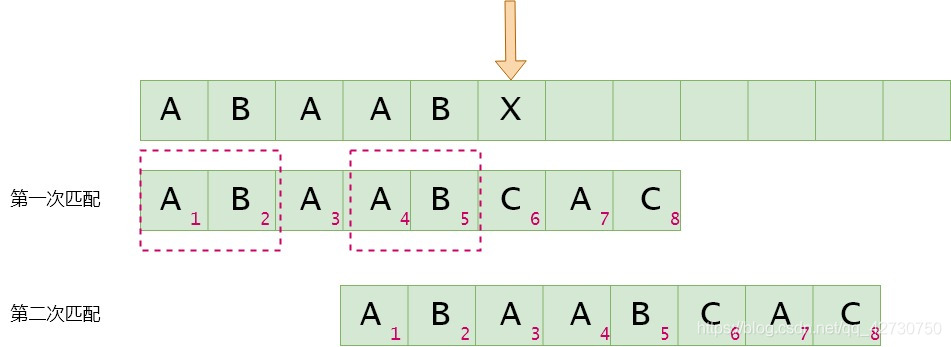
如果模式串6号位与主串当前位不匹配,找最长公共前后缀,指针前面的子串为"ABAAB""ABAAB""ABAAB",即最长公共前后缀为"AB""AB""AB",其长度为2,则下次匹配时将前缀位置移到后缀位置,即模式串3号位与主串的当前位进行比较。next[5]=2
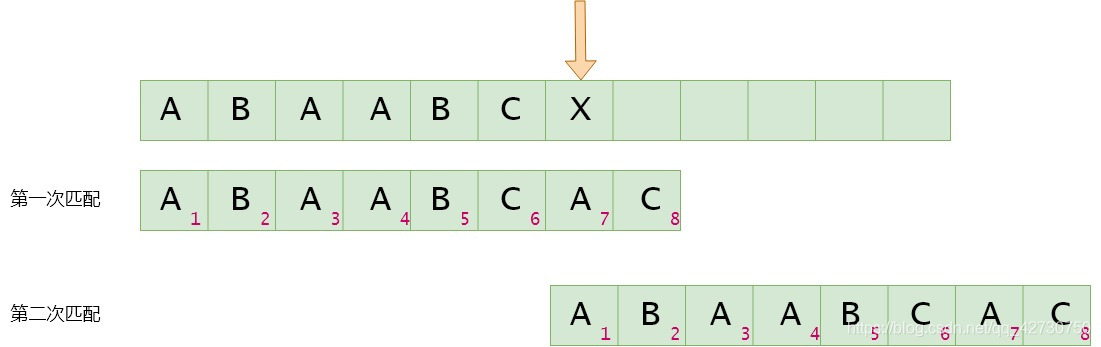
如果模式串7号位与主串当前位不匹配,找最长公共前后缀,指针前面的子串为"ABAABC""ABAABC""ABAABC",即最长公共前后缀为空集,其长度为0,则下次匹配时将模式串1号位与主串的当前位进行比较。next[6]=0
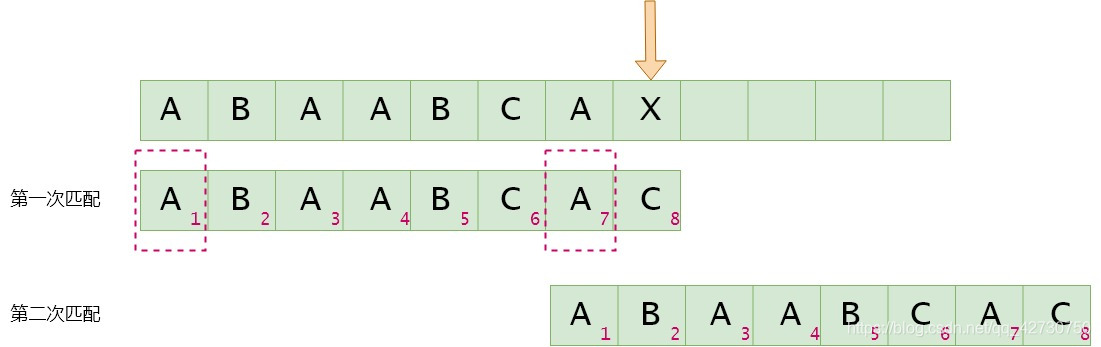
如果模式串8号位与主串当前位不匹配,找最长公共前后缀,指针前面的子串为"ABAABCA""ABAABCA""ABAABCA",即最长公共前后缀为"A""A""A",其长度为1,则下次匹配时将模式串2号位与主串的当前位进行比较。next[7]=1
综上,可以得到模式串的next数组,发现没有,把主串去掉也可以得到这个数组,即下次匹配时模式串向后移动的位数与主串无关,仅与模式串本身有关。
| 位编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 索引 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 模式串 | A | B | A | A | B | C | A | C |
| next | -1 | 0 | 0 | 1 | 1 | 2 | 0 | 1 |
next数组,即存放的是每个字符匹配失败时,对应的下一次匹配时模式串开始匹配的位置。
如何在代码里实现上述流程呢?举个栗子,蓝色方框圈出的就是公共前后缀,假设next[j]=t:
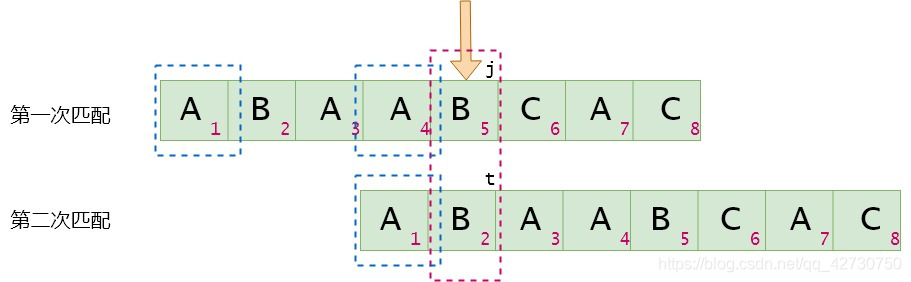
当Tj=TtT_j=T_tTj=Tt时,可以得到next[j+1]=t+1=next[j]+1next[j+1]=t+1=next[j]+1next[j+1]=t+1=next[j]+1。这个时候j=4,t=1j=4,t=1j=4,t=1(索引);
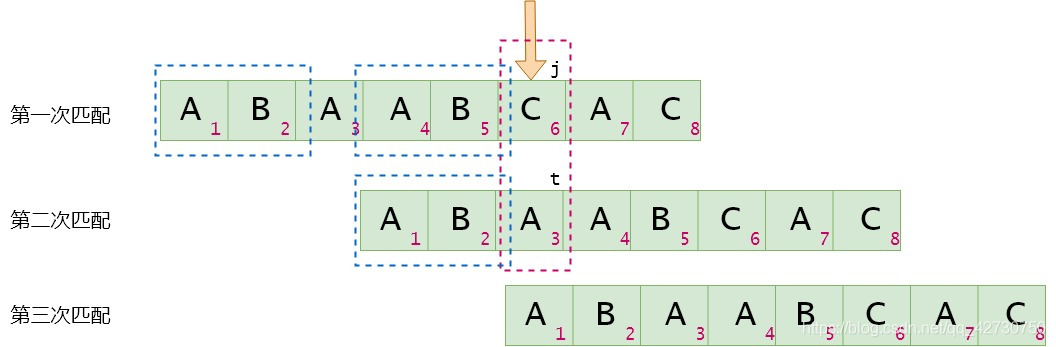
当Tj≠TtT_j \neq T_tTj=Tt时,即模式串ttt位置与主串(并不是真正的主串)不匹配,则将下面的那个模式串移动到next[t]next[t]next[t]位置进行比较,即t=next[t]t=next[t]t=next[t],直到Tj=TtT_j=T_tTj=Tt或t=−1t=-1t=−1,当t=−1t=-1t=−1时,next[j+1]=0next[j+1]=0next[j+1]=0。这里就是t=next[2]=0t=next[2]=0t=next[2]=0,即下次匹配时,模式串的第1位与主串当前位进行比较。
代码如下:
def getNext(substrT):
next_list = [-1 for i in range(len(substrT))]
j = 0
t = -1
while j < len(substrT) - 1:
if t == -1 or substrT[j] == substrT[t]:
j += 1
t += 1
# Tj=Tt, 则可以到的next[j+1]=t+1
next_list[j] = t
else:
# Tj!=Tt, 模式串T索引为t的字符与当前位进行匹配
t = next_list[t]
return next_list
def KMP(substrS, substrT, next_list):
count = 0
j = 0
t = 0
while j < len(substrS) and t < len(substrT):
if substrS[j] == substrT[t] or t == -1:
# t == -1目的就是第一位匹配失败时
# 主串位置加1, 匹配串回到第一个位置(索引为0)
# 匹配成功, 主串和模式串指针都后移一位
j += 1
t += 1
else:
# 匹配失败, 模式串索引为t的字符与当前位进行比较
count += 1
t = next_list[t]
if t == len(substrT):
# 这里返回的是索引
return j - t, count+1
else:
return -1, count+1
3. KMP算法优化版
上面定义的next数组在某些情况下还有些缺陷,发现没有,在第一个图中,我们还可以跳过第3次匹配,直接进行第4次匹配。为了更好地说明问题,我们以下面这种情况为例,来优化一下KMP算法。假设主串S=AAABAAAABS=AAABAAAABS=AAABAAAAB,模式串T=AAAABT=AAAABT=AAAAB,按照KMP算法,匹配过程如下:
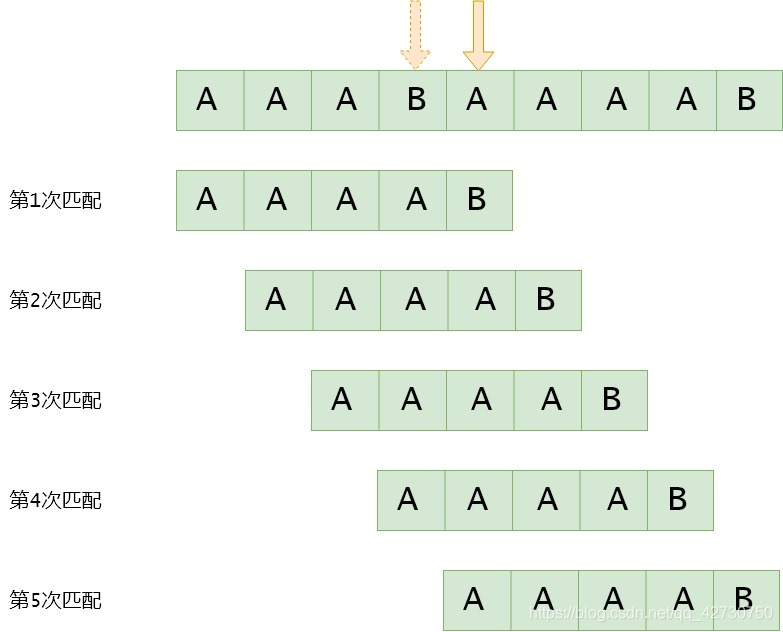
可以看到第2、3、4次的匹配是多余的,因为我们在第一次匹配时,主串SSS的4号位为模式串TTT的4号位就已经比较了,且T3≠S3T_3 \neq S_3T3=S3,又因为模式串TTT的4号位与其1、2、3号位的字符一样,即T3=T2=T1=T0≠S3T_3=T_2=T_1=T_0 \neq S_3T3=T2=T1=T0=S3,所以可以直接进入第5次匹配。
那么,问题出在哪里???我们结合着next数组看一下:
| 位编号 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 索引 | 0 | 1 | 2 | 3 | 4 |
| 模式串 | A | A | A | A | B |
| next | -1 | 0 | 1 | 2 | 3 |
问题在于,当Tj≠SjT_j \neq S_jTj=Sj时,下次匹配的必然是Tnext[j]T_{next[j]}Tnext[j]与SjS_jSj,如果这时Tnext[j]=TjT_{next[j]} = T_jTnext[j]=Tj,那么又相当于TjT_jTj与SjS_jSj进行比较,因为它们的字符一样,毫无疑问,这次匹配是没有意义的,应当将next[j]next[j]next[j]的值直接赋值为-1,即遇到这种情况,主串与模式串都从下一位开始比较。
所以,我们要修正一下next数组。
大致流程和上面求解next数组时一样,这里就是多了一个判别条件,如果在匹配时出现了Tnext[j]=TjT_{next[j]} = T_jTnext[j]=Tj,我们就将next[j]更新为next[\Big[[next[j]]\Big]],直至两者不相等为止(相当于了迭代)。在代码里面实现就是,如果某个字符已经相等或者第一个next[j]数组值为-1(即t=−1t=-1t=−1),且主串和模式串指针各后移一位时的字符仍然相同,那么就将当前的next[j]值更新为上一个next[j]数组值,更新后的数组命名为nextval。
代码如下:
def getNextval(substrT):
nextval_list = [-1 for i in range(len(substrT))]
j = 0
t = -1
while j < len(substrT) - 1:
if t == -1 or substrT[j] == substrT[t]:
j += 1
t += 1
if substrT[j] != substrT[t]:
# Tj=Tt, 但T(j+1)!=T(t+1), 这个就和next数组计算时是一样的
# 可以得到nextval[j+1]=t+1
nextval_list[j] = t
else:
# Tj=Tt, 且T(j+1)==T(t+1), 这个就是next数组需要更新的
# nextval[j+1]=上一次的nextval_list[t]
nextval_list[j] = nextval_list[t]
else:
# 匹配失败, 模式串索引为t的字符与当前位进行比较
t = nextval_list[t]
return nextval_list
对KMP的优化其实就是对next数组的优化,修正后的next数组,即nextval数组如下:
| 位编号 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 索引 | 0 | 1 | 2 | 3 | 4 |
| 模式串 | A | A | A | A | B |
| nextval | -1 | -1 | -1 | -1 | 3 |
下面就测试一下:
if __name__ == '__main__':
S1 = 'ABACABAB'
T1 = 'ABAB'
S2 = 'AAABAAAAB'
T2 = 'AAAAB'
print('*' * 50)
print('主串S={0}与模式串T={1}进行匹配'.format(S1, T1))
print('{:*^25}'.format('KMP'))
next_list1 = getNext(T1)
print('next数组为: {}'.format(next_list1))
index1_1, count1_1 = KMP(S1, T1, next_list1)
print('匹配到的位置(索引): {}, 匹配次数: {}'.format(index1_1, count1_1))
print('{:*^25}'.format('KMP优化版'))
nextval_list1 = getNextval(T1)
print('nextval数组为: {}'.format(nextval_list1))
index1_2, count1_2 = KMP(S1, T1, nextval_list1)
print('匹配到的位置(索引): {}, 匹配次数: {}'.format(index1_2, count1_2))
print('')
print('*' * 50)
print('主串S={0}与模式串T={1}进行匹配'.format(S2, T2))
print('{:*^25}'.format('KMP'))
next_list2 = getNext(T2)
print('next数组为: {}'.format(next_list2))
index2_1, count2_1 = KMP(S2, T2, next_list2)
print('匹配到的位置(索引): {}, 匹配次数: {}'.format(index2_1, count2_1))
print('{:*^25}'.format('KMP优化版'))
nextval_list2 = getNextval(T2)
print('nextval数组为: {}'.format(nextval_list2))
index2_2, count2_2 = KMP(S2, T2, nextval_list2)
print('匹配到的位置(索引): {}, 匹配次数: {}'.format(index2_2, count2_2))
运行结果如下:
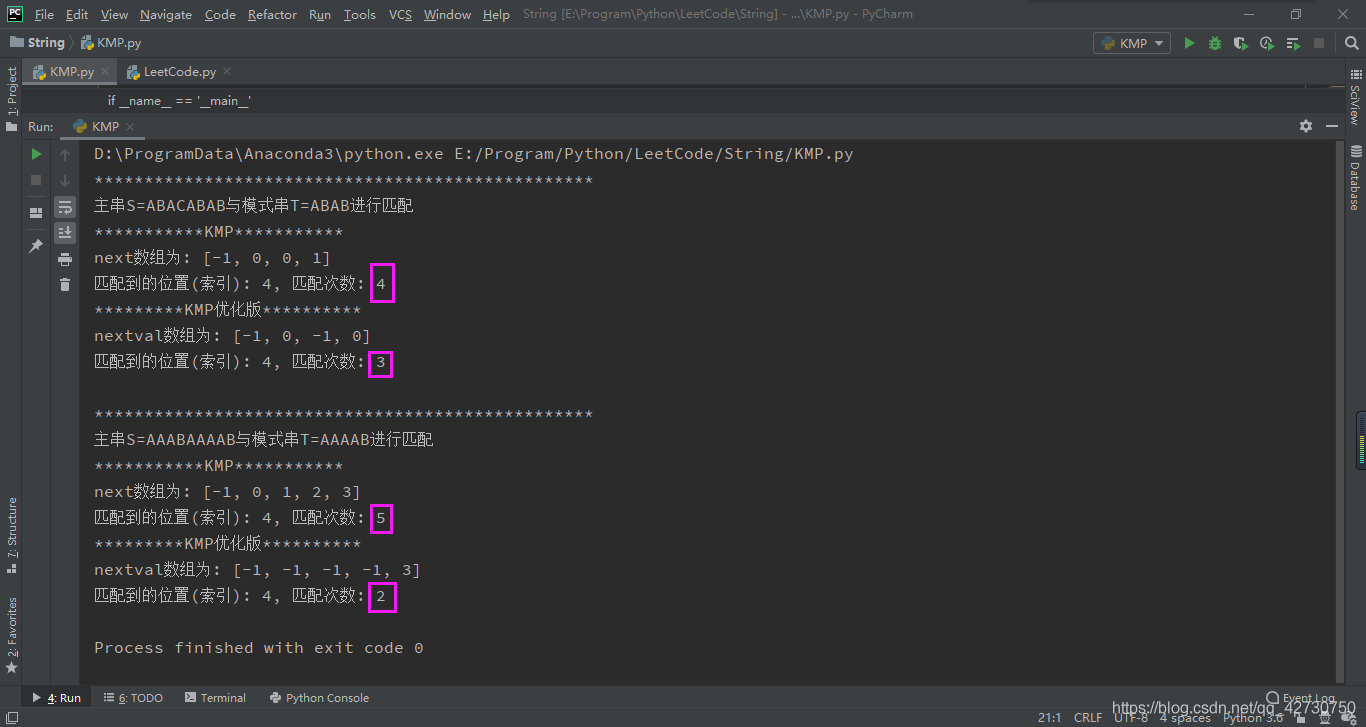
运行的结果和我们分析的是一样的,不修正next数组时,主串S=ABACABABS=ABACABABS=ABACABAB与模式串T=ABABT=ABABT=ABAB匹配时需要4次,主串S=AAABAAAABS=AAABAAAABS=AAABAAAAB与模式串T=AAAABT=AAAABT=AAAAB匹配时需要5次;修正next数组后,主串S=ABACABABS=ABACABABS=ABACABAB与模式串T=ABABT=ABABT=ABAB匹配时需要3次,主串S=AAABAAAABS=AAABAAAABS=AAABAAAAB与模式串T=AAAABT=AAAABT=AAAAB匹配时仅需要2次。
结束语
在写本篇博客之前也是反复看参考书、视频,边画图边去理解它,这篇博客也是反复修改了好几次,最终算是把KMP解决掉了,有关字符串知识的复习也算是基本结束,下面就是刷题了(虽然在LeetCode做过了几道题)。
到此这篇关于Python描述数据结构之KMP篇的文章就介绍到这了,更多相关Python KMP内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们!

