Matplotlib可视化之自定义颜色绘制精美统计图
自定义颜色
在生活中,我们可能对色彩的搭配与审美有自己的偏好,因此,我们可能希望matplotlib遵循自定义的颜色方案,以便所绘制的图形更好地适合文档或网页。
matplotlib中有多种定义颜色的方法,常见的方法包括:
1.三元组(Triplets):颜色可以描述为一个实数三元组,即颜色的红、蓝、绿分量,其中每个分量在[0,1]区间内。因此,(1.0, 0.0, 0.0)表示纯红色,而(1.0, 0.0, 1.0)则表示粉色。
2.四元组(Quadruplets):它们前三个元素与三元组定义相同,第四个元素定义透明度值。此值也在[0,1]区间内。将图形渲染到图片文件中时,使用透明颜色可以使绘制图形与背景进行混合。
3.预定义名称:matplotlib将标准HTML颜色名称解释为实际颜色。例如,字符串red即可表示为红色。同时一些某些颜色的具有简洁的别名,如下表所示:
| 别名 | 颜色 | 显示 |
| b | blue | |
| g | green | |
| r | red | |
| c | cyan | |
| m | magenta | |
| y | yellow | |
| k | black | |
| w | white |
4.HTML颜色字符串:matplotlib可以将HTML颜色字符串解释为实际颜色。这些字符串被定义为#RRGGBB,其中RR、GG和BB是使用十六进制编码的红色、绿色和蓝色分量。
5.灰度字符串:matplotlib将浮点值的字符串表示形式解释为灰度,例如0.75表示中浅灰色。
使用自定义颜色绘制曲线图
通过设置plt.plot()函数的参数color(或等效的简写为c),可以设置曲线的颜色,如下所示:
import numpy as np
import matplotlib.pyplot as plt
def pdf(x, mu, sigma):
a = 1. / (sigma * np.sqrt(2. * np.pi))
b = -1. / (2. * sigma ** 2)
return a * np.exp(b * (x - mu) ** 2)
x = np.linspace(-6, 6, 1000)
for i in range(5):
samples = np.random.standard_normal(50)
mu, sigma = np.mean(samples), np.std(samples)
plt.plot(x, pdf(x, mu, sigma), color = str(.15*(i+1)))
plt.plot(x, pdf(x, 0., 1.), color = 'k')
plt.plot(x, pdf(x, 0.2, 1.), color = '#00ff00')
plt.plot(x, pdf(x, 0.4, 1.), color = (0.9,0.9,0.0))
plt.plot(x, pdf(x, 0.4, 1.), color = (0.9,0.9,0.0,0.8))
plt.show()

使用自定义颜色绘制散点图
可以以同样的方式像控制曲线图一样控制散点图的颜色。有两种可用的形式:
1.为所有点使用相同的颜色 :所有点都将以相同的颜色显示。
2.为每个点定义不同的颜色:为每个点提供不同的颜色。
为所有点使用相同的颜色
利用从二元高斯分布中提取的两组点y_1和y_2,每一组中点的颜色相同:
import numpy as np import matplotlib.pyplot as plt y_1 = np.random.standard_normal((150, 2)) y_1 += np.array((-1, -1)) # Center the distrib. at <-1, -1> y_2 = np.random.standard_normal((150, 2)) y_2 += np.array((1, 1)) # Center the distrib. at <1, 1> plt.scatter(y_1[:,0], y_1[:,1], color = 'c') plt.scatter(y_2[:,0], y_2[:,1], color = 'b') plt.show()

为每个点定义不同的颜色
我们总会遇到这样的绘图场景,需要为不同类别的点使用不同的颜色进行绘制,以观察不同类别间的差异情况。以Fisher's iris数据集为例,其数据集中数据类似如下所示:
5.0,3.3,1.4,0.2,Iris-setosa 7.0,3.2,4.7,1.4,Iris-versicolo
数据集的每个点都存储在以逗号分隔的列表中。最后一列给出每个点的标签(标签包含三类:Iris-virginica、Iris-versicolor 和Iris-Vertosa)。在示例中,这些点的颜色将取决于它们的标签,如下所示:
import numpy as np
import matplotlib.pyplot as plt
label_set = (
b'Iris-setosa',
b'Iris-versicolor',
b'Iris-virginica',
)
def read_label(label):
return label_set.index(label)
data = np.loadtxt('iris.data', delimiter = ',', converters = { 4 : read_label })
color_set = ('c', 'y', 'm')
color_list = [color_set[int(label)] for label in data[:,4]]
plt.scatter(data[:,0], data[:,1], color = color_list)
plt.show()

Tips:
对于三种可能的标签,分别指定一种唯一的颜色。颜色在color_set中定义,标签在label_set中定义。label_set中的第i个标签与color_set中的第i个颜色相关联。然后我们利用它们把标签列表转换成颜色列表color_list。然后只需调用plt.scatter()一次即可显示所有点及其颜色。我们也可以通过对三个不同的类别单独调用plt.scatter()来实现,但这将需要更多的代码。另外需要注意的是:如果两点有可能有相同的坐标,但有不同的标签,显示的颜色将是后绘制点的颜色,可以使用透明颜色,用来显示重叠点。
为散点图中数据点的边使用自定义颜色
与color参数控制点的颜色一样,可以使用edgecolor参数控制数据点的边的颜色。可以为每个点的边设置相同的颜色:
import numpy as np import matplotlib.pyplot as plt data = np.random.standard_normal((100, 2)) plt.scatter(data[:,0], data[:,1], color = '1.0', edgecolor='r') plt.show()

Tips:也可以像在为每个点定义不同的颜色部分中介绍的一样为每个点的边设置不边的颜色
使用自定义颜色绘制条形图
控制绘制条形图使用的颜色与曲线图和散点图的工作原理相同,即通过可选参数color:
import numpy as np import matplotlib.pyplot as plt w_pop = np.array([5., 30., 45., 22.]) m_pop = np.array( [5., 25., 50., 20.]) x = np.arange(4) plt.barh(x, w_pop, color='m') plt.barh(x, -m_pop, color='c') plt.show()
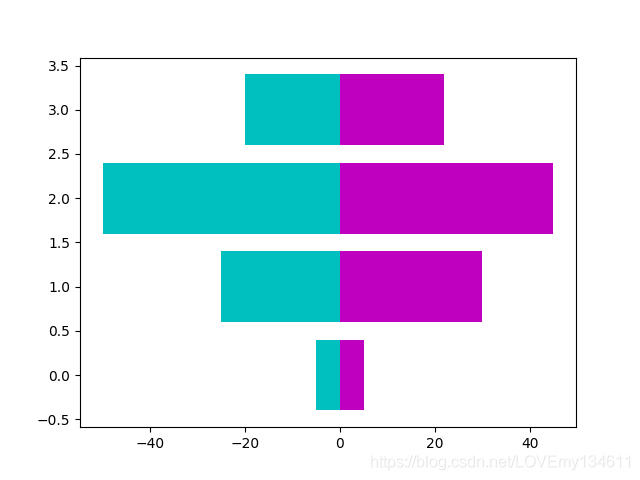
Tips:
使用pyplot.bar()和pyplot.barh()函数自定义颜色绘制条形图的工作方式与pyplot.scatter()完全相同,只需设置可选参数color,同时也可以参数edgecolor控制条形边的颜色。
import numpy as np
import matplotlib.pyplot as plt
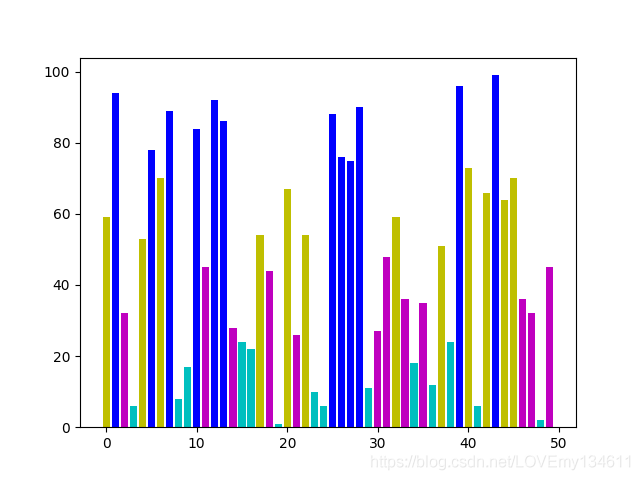
values = np.random.random_integers(99, size = 50)
color_set = ('c', 'm', 'y', 'b')
color_list = [color_set[(len(color_set) * val) // 100] for val in values]
plt.bar(np.arange(len(values)), values, color = color_list)
plt.show()
使用自定义颜色绘制饼图
自定义饼图颜色的方法类似于条形图:
import numpy as np
import matplotlib.pyplot as plt
color_set = ('c', 'm', 'y', 'b')
values = np.random.rand(6)
plt.pie(values, colors = color_set)
plt.show()
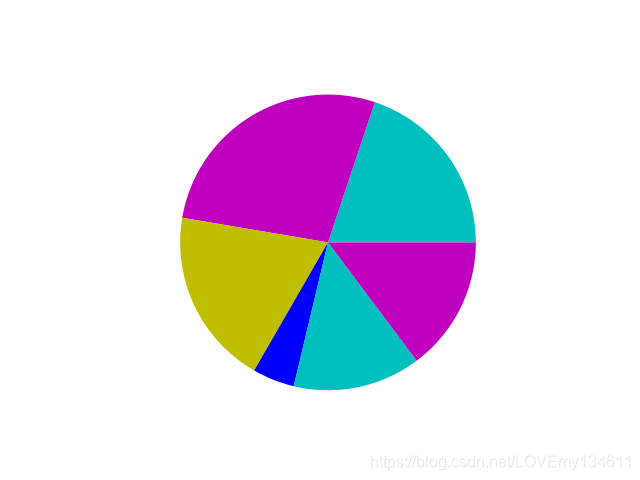
Tips:
饼图接受使用colors参数(注意,此处是colors,而不是在plt.plot()中使用的color)的颜色列表。但是,如果颜色数少于输入值列表中的元素数,那么plt.pie()将循环使用颜色列表中的颜色。在示例中,使用包含四种颜色的列表,为包含六个值的饼图着色,因此,其中有两个颜色将使用两次。
使用自定义颜色绘制箱型图
将箱型图中线条颜色进行修改:
import numpy as np
import matplotlib.pyplot as plt
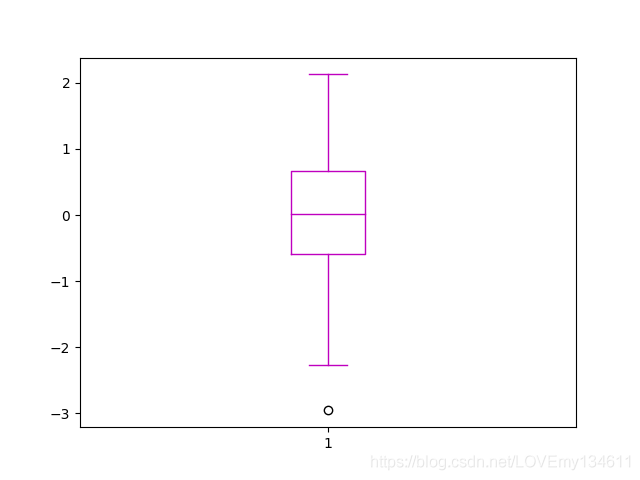
values = np.random.randn(100)
b = plt.boxplot(values)
for name, line_list in b.items():
for line in line_list:
line.set_color('m')
plt.show()
使用色彩映射绘制散点图
如果要在图形中使用多种颜色,逐个定义每种颜色并不是最佳方案,色彩映射可以解决此问题。色彩映射用一个变量对应一个值(颜色)的连续函数定义颜色。matplotlib提供了几种常见的颜色映射;大多数是连续的颜色渐变。
色彩映射在matplotib.cm模块中定义,提供创建和使用色彩映射的函数,它还提供了预定义的色彩映射选择。
函数pyplot.scatter()接受color参数的值列表,当提供cmap参数时,这些值将被解释为色彩映射的索引:
import numpy as np import matplotlib.cm as cm import matplotlib.pyplot as plt n = 256 angle = np.linspace(0, 8 * 2 * np.pi, n) radius = np.linspace(.5, 1., n) x = radius * np.cos(angle) y = radius * np.sin(angle) plt.scatter(x, y, c = angle, cmap = cm.hsv) plt.show()

Tips:在matplotlib.cm模块中提供了大量预定义的色彩映射,其中cm.hsv包含全光谱的颜色。
使用色彩映射绘制条形图
plt.scatter()函数内置了对色彩映射的支持,其他一些绘图函数也内置支持色彩映射。但是,有些函数(如pyplot.bar())并未内置对色彩映射的支持。但是matplotlib可以从颜色映射显式生成颜色:
import numpy as np import matplotlib.cm as cm import matplotlib.pyplot as plt import matplotlib.colors as col values = np.random.random_integers(99, size = 50) cmap = cm.ScalarMappable(col.Normalize(0, 99), cm.binary) plt.bar(np.arange(len(values)), values, color = cmap.to_rgba(values)) plt.show()

Tips:首先创建色彩映射cmap,以便将[0, 99]范围内的值映射到matplotlib.cm.binary的颜色。然后,函数cmap.to_rgba将值列表转换为颜色列表。因此,尽管plt.bar并未内置色彩映射支持,但依旧可以使用并不复杂的代码实现色彩映射。
创建自定义配色方案
matplotlib使用的默认颜色考虑的主要对象是打印文档或出版物。因此,默认情况下,背景为白色,而标签、轴和其他注释则显示为黑色,在某些不同的使用环境中,我们可能需要使用的配色方案;例如,将图形背景设置为黑色,注释设置为白色。
在matplotlib中,各种对象(如轴、图形和标签)都可以单独修改。但逐个更改这些对象的颜色配置并非最佳方案。在matplotlib中,所有对象都可以利用集中式配置修改其默认颜色:
import numpy as np
import matplotlib as mpl
from matplotlib import pyplot as plt
mpl.rc('lines', linewidth = 2.)
mpl.rc('axes', facecolor = 'k', edgecolor = 'w')
mpl.rc('xtick', color = 'w')
mpl.rc('ytick', color = 'w')
mpl.rc('text', color = 'w')
mpl.rc('figure', facecolor = 'k', edgecolor ='w')
mpl.rc('axes', prop_cycle = mpl.cycler(color=[(0.1, .5, .75),(0.5, .5, .75)]))
x = np.linspace(0, 7, 1024)
plt.plot(x, np.sin(x))
plt.plot(x, np.cos(x))
plt.show()

到此这篇关于Matplotlib可视化之自定义颜色绘制精美统计图的文章就介绍到这了,更多相关Matplotlib绘制统计图内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们!

