python机器学习基础线性回归与岭回归算法详解

目录

• 一、什么是线性回归
• 1.线性回归简述
• 2.数组和矩阵
• 数组
• 矩阵
• 3.线性回归的算法
• 二、权重的求解
• 1.正规方程
• 2.梯度下降
• 三、线性回归案例
• 1.案例概述
• 2.数据获取
• 3.数据分割
• 4.数据标准化
• 5.模型训练
• 6.回归性能评估
• 7.梯度下降与正规方程区别
• 四、岭回归Ridge
• 1.过拟合与欠拟合
• 2.正则化

一、什么是线性回归

1.线性回归简述

线性回归，是一种趋势，通过这个趋势，我们能预测所需要得到的大致目标值。线性关系在二维中是直线关系，三维中是平面关系。

我们可以使用如下模型来表示线性回归：y = wx+b（w是权重，x是特征，b是偏置项）

当有多个特征时，线性关系模型如下图所示：

2.数组和矩阵

数组

数组可以是多维的，各个维度的数组表示如下：

0维：5

1维：[1,2,5,5,4,8]

2维：[[1,4,5],[1,4,7]]

3维：[[[1,4,5],[1,4,7]],[[1,4,5],[1,4,7]]]

数组运算有加法，乘法。具体计算可以在python中尝试，数组是ndarray类型。3.

矩阵

矩阵特点：必须是二维，矩阵的运算满足了特定的需求。我们可以仅仅通过1步的矩阵乘法，就得出w1*x1+w2*x2+w3*x3这样模型的结果。

矩阵乘法的要求会涉及到矩阵的形状要求：m*n的矩阵 * n*p的矩阵，结果是m*p的矩阵

也就是说，第一个矩阵的列数，必须要和第二个矩阵的行数相同。

3.线性回归的算法

线性回归是一种迭代的算法。我们需要建立一个函数，对于每一个特征x(i)都有一个对应的权重w(i)，两者相乘，并最终把所有的特征权重乘积求和，就是我们的目标结果。但如何寻找到最佳的权重，从而使得模型能够最好地拟合我们的样本呢？

线性回归的迭代算法的每次迭代，都会更新权重w(i)的值，使模型往靠近样本点的地方更加靠近，而损失函数，就是我们用来求得最佳权重的函数。

损失函数定义如下：

损失意思就是预测的各个目标值，与各个原目标值的差的平方和（误差平方和）。损失越小也就是预测值与原值越接近，效果越好。该方法也称为最小二乘法。当损失函数达到最小值时，所对应的权重w，就是我们的目标权重。

二、权重的求解

1.正规方程

是求权重w的一种方法，适用于特征少的数据。用的比较少。

2.梯度下降

该方法通过指定学习率，并利用梯度，迭代更新权重。通常都使用这个方法。

正规方程API：sklearn.linear_model.LinearRegression()

梯度下降API：sklearn.linear_model.SGDRegressor()

两个算法都可以通过.coef_得到回归系数，学习率是一个超参数，也可使用网格交叉验证进行调优。

三、线性回归案例

1.案例概述

通过从sklearn中获取的“波士顿房价预测”数据进行房价预测，特征有很多，比如该镇的人均犯罪率、一氧化氮浓度、低收入人群占比等。我们对每一个特征都给出一个权重，通过算法，求得最佳的权重即可。

2.数据获取

导入数据代码：

from sklearn.datasets import load_boston
lb = load_boston()

3.数据分割

x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)

4.数据标准化

此处的数据，需要对特征数据以及目标值数据都进行标准化，并且需要用不同的标准。

导入标准化方法:from sklearn.preprocessing import StandardScaler

x实例化方法：std_x = StandardScaler()

y实例化方法：std_y = StandardScaler()

标准化：

x_train = std_x.fit_transform(x_train)

x_test = std_x.transform(x_test)

y_train = std_y.fit_transform(y_train)

y_test = std_y.transform(y_test)

5.模型训练

注意，训练后得出的目标值，是标准化后的，因此需要使用StandardScaler中的inverse_transform进行转换回原来的值。

实例化算法：lr = LinearRegressor()

将数据转为二维：y_train = y_train.reshape(-1,1)

训练算法：lr.fit(x_train, y_train)

预测结果：y_predict = lr.predict(x_test)

结果转为正常结果：y_lr_predict = std.inverse_transform(y_predict)

6.回归性能评估

通过对预测值也真实值计算均方误差可得，API中，输入真实目标值，以及预测目标值即可（注意：输入的都是标准化之前的值。

API：sklearn.metrics.mean_squared_error(y_true, y_pred)

线性回归性能评估：mean_squared_error(y_test, y_lr_predict)

以上为使用线性回归算法，对房价进行的预测。其他的算法，具体操作基本一致。

7.梯度下降与正规方程区别

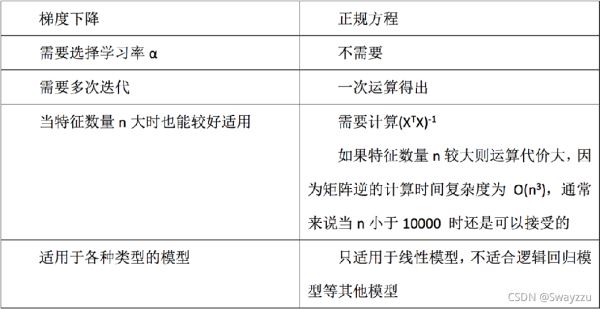
特点：线性回归器是最为简单、易用的回归模型。 从某种程度上限制了使用，尽管如此，在不知道特征之间关系的前提下，我们仍然使用线性回归器作为大多数系统的首要选择。

小规模数据可以使用LinearRegression(不能解决拟合问题)以及其它

大规模数据需要使用梯度下降法，SGDRegressor

四、岭回归Ridge

1.过拟合与欠拟合

欠拟合：一个假设在训练数据上不能获得更好的拟合， 但是在训练数据外的数据集上也不能很好地拟合数据，此时认为这个假设出现了欠拟合的现象。(模型过于简单)

解决方法：增加特征

过拟合：一个假设在训练数据上能够获得比其他假设更好的拟合， 但是在训练数据外的数据集上却不能很好地拟合数据，此时认为这个假设出现了过拟合的现象。(模型过于复杂)

解决方法：正则化

2.正则化

L2正则化是通过减少权重的方式，对模型进行优化，以解决过拟合的问题。该方法可以使得权重的每个元素都非常接近于0，参数变小，则模型变简单。从而达到解决过拟合问题的效果。

岭回归就是带有正则化的线性回归。

岭回归API:sklearn.linear_model.Ridge

正则化中，alpha（或者lambda）越大，说明对参数的惩罚越大，参数就越趋近于0。

岭回归优点：回归得到的回归系数更符合实际，更可靠。另外，能让估计参数的波动范围变小，变的更稳定。在存在病态数据偏多的研究中有较大的实用价值。

以上就是python机器学习基础线性回归与岭回归算法详解的详细内容，更多关于python线性回归与岭回归算法的资料请关注我们其它相关文章！