Python+NumPy绘制常见曲线的方法详解

目录
  • 一、利萨茹曲线
  • 二、计算斐波那契数列
  • 三、方波
  • 四、锯齿波和三角波

在NumPy中，所有的标准三角函数如sin、cos、tan等均有对应的通用函数。

一、利萨茹曲线

（Lissajous curve）利萨茹曲线是一种很有趣的使用三角函数的方式(示波器上显示出利萨茹曲线)。利萨茹曲线由以下参数方程定义：

x = A sin(at + n/2)

y = B sin(bt)

利萨茹曲线的参数包括 A 、 B 、 a 和 b 。为简单起见，我们令 A 和 B 均为1,设置的参数为 a=9 ， b=8

import numpy as np
import matplotlib.pyplot as plt

A=B=1
a=9
b=8

t = np.linspace(-np.pi, np.pi, 201)  #使用linspace函数初始化变量t
x = np.sin(a * t + np.pi/2)  # sin 函数和NumPy常量 pi 计算变量 x
y = np.sin(b * t)  # sin函数计算变量y
plt.plot(x, y)
plt.show()

运行结果：

二、计算斐波那契数列

斐波那契数列的递推关系可以用矩阵来表示。斐波那契数列的计算等价于矩阵的连乘。可用两种方法计算了斐波那契数列

1）黄金比例计算方法，使用 rint 函数对浮点数取整但不改变浮点数类型

1，1，2，3，5，8，13，21，34，55，89，……

#   斐波那契数,用黄金分割公式或通常所说的比奈公式，加上取整函数
n = np.arange(1, 9)
sqrt5 = np.sqrt(5)
phi = (1 + sqrt5)/2 #利用根号5计算黄金比例，或者直接用phi=1+0.618
print("比例：",phi)
print('\n')
fibonacci = np.rint((phi**n - (-1/phi)**n)/sqrt5)  #用rint()函数对浮点数取整但不改变浮点数类型
print("Fibonacci", fibonacci)

2）利用矩阵进行计算：用 matrix 函数创建矩阵

# 斐波那契数,用矩阵来表示斐波那契数列的递推关系
F = np.matrix([[1, 1], [1, 0]])
print ("8th Fibonacci:", (F ** 10)[0, 0])

运行结果：

比例： 1.618033988749895

Fibonacci [ 1.  1.  2.  3.  5.  8. 13. 21.]
8th Fibonacci: 89

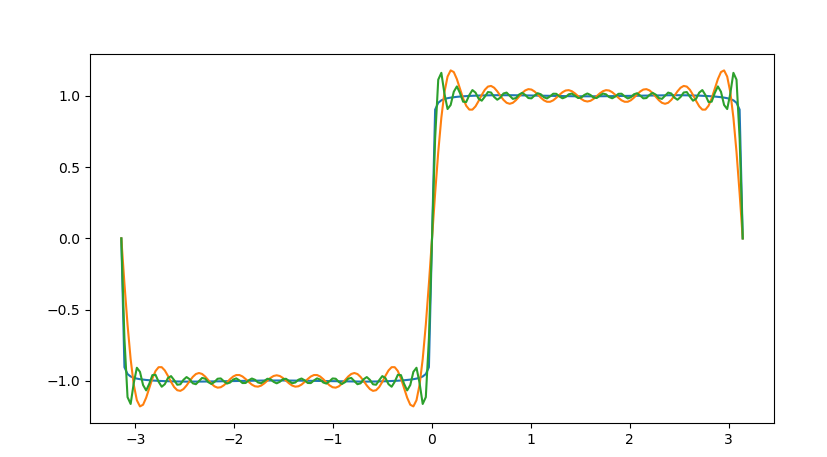
三、方波

方波可以近似表示为多个正弦波的叠加。任意一个方波信号都可以用无穷傅里叶级数来表示。

需要累加很多项级数，且级数越多结果越精确，这里取 k=99（可以分别设置为9，50，1000等进行测试观察生成效果） 以保证足够的精度。绘制方波的步骤如下。

1) 初始化 t 和 k 开始，并将函数值初始化为

m = np.linspace(-np.pi, np.pi, 201) #从 -pi 到 pi 上均匀分布的 201 个点
k = np.arange(1,99)   # k=99 以保证足够的精度，如图中的9 20 99显示的波形
k = 2 * k - 1
f = np.zeros_like(m)

2）使用 sin()求正弦函数，用sum()数计算各项级数：

for i in range(len(m)):  #使用 sin 和 sum 函数进行计算
    f[i] = np.sum(np.sin(k * m[i])/k)
f = (4 / np.pi) * f

3）绘制波形

plt.plot(t, f)
plt.show()

四、锯齿波和三角波

锯齿波和三角波也是常见的波形。和方波类似，也可以将它们表示成无穷傅里叶级数。对锯齿波取绝对值即可得到三角波。锯齿波的无穷级数表达式如下：

import numpy as np
import matplotlib.pyplot as plt

t = np.linspace(-np.pi, np.pi, 201)
k = np.arange(1, 99)
f = np.zeros_like(t)
for i in range(len(t)):
    f[i] = np.sum(np.sin(2 * np.pi * k * t[i])/k)

f = (-2 / np.pi) * f
plt.plot(t, f, lw=1.0)
plt.plot(t, np.abs(f), lw=2.0)
plt.show()

运行结果：

以上就是Python+NumPy绘制常见曲线的方法详解的详细内容，更多关于Python NumPy绘制曲线的资料请关注我们其它相关文章！

赞 (0)

相关推荐

  • Python实现曲线拟合操作示例【基于numpy,scipy,matplotlib库】

    Python实现曲线拟合操作示例【基于numpy,scipy,matplotlib库】

    本文实例讲述了Python实现曲线拟合操作.分享给大家供大家参考,具体如下: 这两天学习了用python来拟合曲线. 一.环境配置 本人比较比较懒,所以下载的全部是exe文件来安装,安装按照顺利来安装.自动会找到python的安装路径,一直点下一步就行.还有其他的两种安装方式:一种是解压,一种是pip.我没有尝试,就不乱说八道了. 没有ArcGIS 环境的,可以不看下面这段话了. 在配置环境时遇见一个小波折,就是原先电脑装过ArcGIS10.2 ,所以其会默认安装python2.7,而且pyth

  • 详解如何利用Python绘制科赫曲线

    详解如何利用Python绘制科赫曲线

    目录 1. 递归 1.1 定义 1.2 数学归纳法 2. 递归的使用方法 2.1 阶乘 2.2 字符串反转 3. 科赫曲线的绘制 3.1 概要 3.2 绘制科赫曲线 3.3 科赫曲线的雪花效果 3.4 分形几何 1. 递归 1.1 定义 函数作为一种代码封装, 可以被其他程序调用,当然,也可以被函数内部代码调用.这种函数定义中调用函数自身的方式称为递归.就像一个人站在装满镜子的房间中,看到的影像就是递归的结果.递归在数学和计算机应用上非常强大,能够非常简洁地解决重要问题. 数学上有个经典的递归例

  • 使用Python绘制三种概率曲线详解

    目录 曲线一 解释 代码实现 曲线二 解释 代码实现 曲线三 代码实现 曲线一 解释 这里是使用matplotlib来绘制正态分布的曲线. 代码实现 import numpy as np import matplotlib.pyplot as plt def test1(n, m=500): out = [] result = np.random.normal(1, 5, n * m) print(result) for i in range(m): average0 = 0 for j in

  • Python曲线平滑的实现示例

    Python曲线平滑的实现示例

    在编写测试程序的时候,由于数据帧数多的原因,导致生成的曲线图比较难看,如下图: 由于高频某些点的波动导致高频曲线非常难看,因此需要对曲线做平滑处理,让曲线过渡更平滑.对曲线进行平滑处理,这里推荐使用Savitzky-Golay 滤波器,可以在scipy库里直接调用,不需要再定义函数. Python中 Savitzky-Golay 滤波器调用如下: tmp_smooth = scipy.signal.savgol_filter(tmp,53,3) scipy函数解释:scipy.signal.sa

  • 利用python实现蝴蝶曲线

    利用python实现蝴蝶曲线

    目录 一.什么是蝴蝶曲线? 二.画一个最简单的蝴蝶曲线 三.画一个优美的蝴蝶曲线 导言: 接上期,我们在极坐标下用python画了圆,心形线,玫瑰线,阿基米德螺线和双纽线5大常规曲线外,后来发现还漏了好一些漂亮且有意思的的曲线,今天就来讲一讲蝴蝶曲线. 一.什么是蝴蝶曲线? 蝴蝶曲线是平面上一类代数曲线,最初由美国南密西西比大学特普尔·费伊(Temple H·Fay)发现,因其形状宛如一只翩翩起舞的蝴蝶,故为其取美日“蝴蝶曲线”. 极坐标系下蝴蝶曲线方程为: 使用参数方程描述为: 二.画一个最简

  • Python+NumPy绘制常见曲线的方法详解

    Python+NumPy绘制常见曲线的方法详解

    目录 一.利萨茹曲线 二.计算斐波那契数列 三.方波 四.锯齿波和三角波 在NumPy中,所有的标准三角函数如sin.cos.tan等均有对应的通用函数. 一.利萨茹曲线 (Lissajous curve)利萨茹曲线是一种很有趣的使用三角函数的方式(示波器上显示出利萨茹曲线).利萨茹曲线由以下参数方程定义: x = A sin(at + n/2) y = B sin(bt) 利萨茹曲线的参数包括 A . B . a 和 b .为简单起见,我们令 A 和 B 均为1,设置的参数为 a=9 , b=

  • Python+matplotlib绘制多子图的方法详解

    Python+matplotlib绘制多子图的方法详解

    目录 本文速览 1.matplotlib.pyplot api 方式添加子图 2.面向对象方式添加子图 3.matplotlib.pyplot add_subplot方式添加子图 4.matplotlib.gridspec.GridSpec方式添加子图 5.子图中绘制子图 6.任意位置绘制子图(plt.axes) 本文速览 matplotlib.pyplot api 绘制子图 面向对象方式绘制子图 matplotlib.gridspec.GridSpec绘制子图 任意位置添加子图 关于pyplo

  • Python+matplotlib实现循环作图的方法详解

    Python+matplotlib实现循环作图的方法详解

    目录 一.前言 二.实现过程 三.总结 大家好,我是皮皮. 一.前言 前几天在Python白银交流群[在 途中要勤奋的熏肉肉]问了一道Python可视化处理的问题,如下图所示. 原始代码,如下所示: import pandas as pd import numpy as np import matplotlib.pyplot as plt import scipy.stats as st result_parameter_peak = pd.read_csv("result_parameter_

  • Python+Matplotlib绘制3D图像的示例详解

    Python+Matplotlib绘制3D图像的示例详解

    目录 1. 绘制3D柱状图 2. 绘制3D曲面图 示例1 示例2 3.绘制3D散点图 4. 绘制3D曲线图 1. 绘制3D柱状图 绘制3D柱状图使用的是axes3d.bar()方法. 可能跟我们中学学的有一点不同的是,其语法如下: bar(left, height, zs=0, zdir=‘z’, *args, **kwargs) 其中left表示指向侧边的轴,zs表示指向我们的方向的轴,height即表示高度的轴.这三者都需要是一维的序列对象.在调用相关方法的时候,比如设置轴标签,还有一点需要

  • Python实现提取音乐频谱的方法详解

    Python实现提取音乐频谱的方法详解

    目录 前言 1.准备 2.频谱展示 前言 你有没有经常好奇一些音乐软件的频谱特效是怎么做的,为什么做的这么好看?有没有想试试自己提取音乐频谱并可视化展现出来?今天,咱就结合上次的音乐剪辑操作: 3行Python代码实现剪辑音乐 来简单粗暴地可视化下面这首歌曲的频谱! 1.准备 开始之前,你要确保Python和pip已经成功安装在电脑上,如果没有,可以访问这篇文章:超详细Python安装指南 进行安装. Windows环境下打开Cmd(开始—运行—CMD),苹果系统环境下请打开Terminal(c

  • 对numpy Array [: ,] 的取值方法详解

    NumPy数组是一个多维数组对象,称为ndarray 创建一个numpy数组,如下所示 import numpy as np x=np.array([[1,2,3],[4,5,6],[7,8,9]]) 使用的方法和python中的元表差不多 print(x[0:2]) >>>[[1 2 3] [4 5 6]] print(x[:]) >>>[[1 2 3] [4 5 6] [7 8 9]] #有些比较复杂逗号的用法,不一定需要掌握,知道是什么意思即可 #有时候希望只取某

  • 对Python获取屏幕截图的4种方法详解

    Python获取电脑截图有多种方式,具体如下: PIL中的ImageGrab模块 windows API PyQt pyautogui PIL中的ImageGrab模块 import time import numpy as np from PIL import ImageGrab img = ImageGrab.grab(bbox=(100, 161, 1141, 610)) img = np.array(img.getdata(), np.uint8).reshape(img.size[1]

  • C#绘制实时曲线图的方法详解

    C#绘制实时曲线图的方法详解

    在终端机器上的曲线显示本打算用控件,可控件折腾好长时间也没弄顺,还是自己写的好使,记录下来后面再改进. //绘图部分的定义 Int32 Draw_Top;//绘画Y起点 Int32 Draw_Left;//绘画X起点 Int32 Draw_EdgeWidth;//X边缘宽度 Int32 Draw_EdgeHeight;//Y边缘高度 Int32 Draw_RangeWidth;//绘画范围宽度 Int32 Draw_RangeHeight;//绘画范围高度 Double[] XTDYData =

  • Python自动操作Excel文件的方法详解

    目录 工具 读取Excel文件内容 写入Excel文件内容 Excel文件样式调整 设置表头的位置 设置单元格的宽高 总结 工具 python3.7 Pycharm Excel xlwt&xlrd 读取Excel文件内容 当前文件夹下有一个名为“股票数据.xlsx”的Excel文件,可以按照下列代码方式来操作它. import xlrd # 使用xlrd模块的open_workbook函数打开指定Excel文件并获得Book对象(工作簿) wb = xlrd.open_workbook('股票数

  • Python+OpenCV实现阈值分割的方法详解

    Python+OpenCV实现阈值分割的方法详解

    目录 一.全局阈值 1.效果图 2.源码 二.滑动改变阈值(滑动条) 1.效果图 2.源码 三.自适应阈值分割 1.效果图 2.源码 3.GaussianBlur()函数去噪 四.参数解释 一.全局阈值 原图: 整幅图采用一个阈值,与图片的每一个像素灰度进行比较,重新赋值: 1.效果图 2.源码 import cv2 import matplotlib.pyplot as plt #设定阈值 thresh=130 #载入原图,并转化为灰度图像 img_original=cv2.imread(r'

随机推荐