java 数据结构并查集详解

目录

• 一、概述
• 二、实现
• 2.1 Quick Find实现
• 2.2 Quick Union实现
• 三、优化
• 3.1基于size的优化
• 3.2基于rank优化
• 3.2.1路径压缩（Path Compression ）
• 3.2.2路径分裂（Path Spliting）
• 3.2.3路径减半（Path Halving）

一、概述

并查集：一种树型数据结构，用于解决一些不相交集合的合并及查询问题。例如：有n个村庄，查询2个村庄之间是否有连接的路，连接2个村庄

两大核心：

查找 (Find) : 查找元素所在的集合

合并 (Union) : 将两个元素所在集合合并为一个集合

二、实现

并查集有两种常见的实现思路

快查（Quick Find）

• 查找（Find）的时间复杂度：O（1）
• 合并（Union）的时间复杂度：O（n）

快并（Quick Union）

• 查找（Find）的时间复杂度：O（logn）可以优化至O（a（n））a（n）< 5
• 合并（Union）的时间复杂度：O（logn）可以优化至O（a（n））a（n）< 5

使用数组实现树型结构，数组下标为元素，数组存储的值为父节点的值

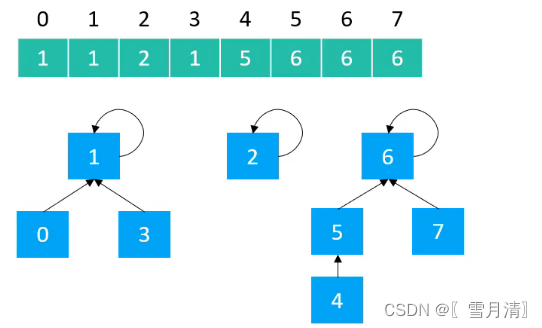
创建抽象类Union Find

public abstract class UnionFind {

	 int[] parents;
	/**
	 * 初始化并查集
	 * @param capacity
	 */
	public UnionFind(int capacity){

		if(capacity < 0) {
			throw new IllegalArgumentException("capacity must be >=0");
		}
        //初始时每一个元素父节点（根结点）是自己
		parents = new int[capacity];
		for(int i = 0; i < parents.length;i++) {
			parents[i] = i;
		}
	}

   /**
     *  检查v1 v2 是否属于同一个集合
     */
	public boolean isSame(int v1,int v2) {
		return find(v1) == find(v2);
	}

    /**
     *  查找v所属的集合 （根节点）
     */
	public  abstract int find(int v);

	/**
     *  合并v1 v2 所属的集合
     */
	public abstract void union(int v1, int v2);

	// 范围检查
	public   void rangeCheck(int v)  {
		if(v<0 || v > parents.length)
			throw new IllegalArgumentException("v is out of capacity");
	}
}

2.1 Quick Find实现

以Quick Find实现的并查集，树的高度最高为2，每个节点的父节点就是根节点

public class UnionFind_QF extends UnionFind {
	public UnionFind_QF(int capacity) {
		super(capacity);

	}

  // 查
@Override
	public  int  find(int v) {
		rangeCheck(v);
		return parents[v];
	}

 // 并 将v1所在集合并到v2所在集合上
@Override
public void union(int v1, int v2) {
    // 查找v1 v2 的父（根）节点
	int p1= find(v1);
	int p2 = find(v2);
	if(p1 == p2) return;

    //将所有以v1的根节点为根节点的元素全部并到v2所在集合上 即父节点改为v2的父节点
	for(int i = 0; i< parents.length; i++) {
		if(parents[i] == p1) {
			parents[i] = p2;
		}
	}

  }
}

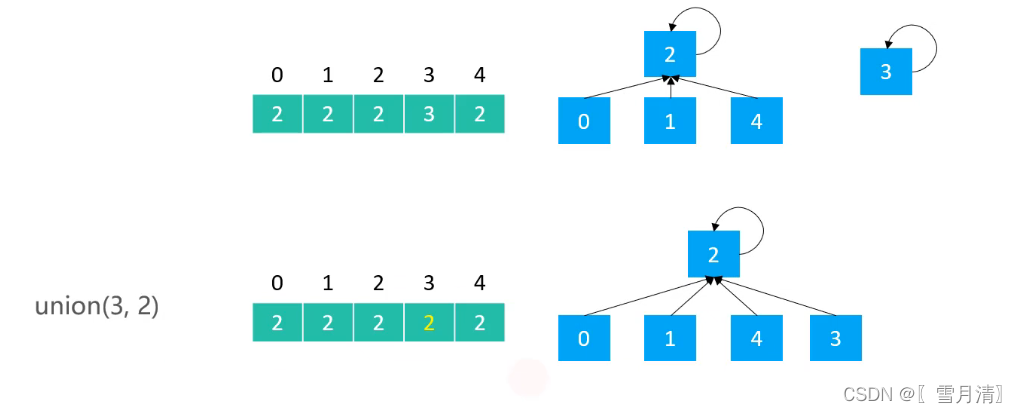
2.2 Quick Union实现

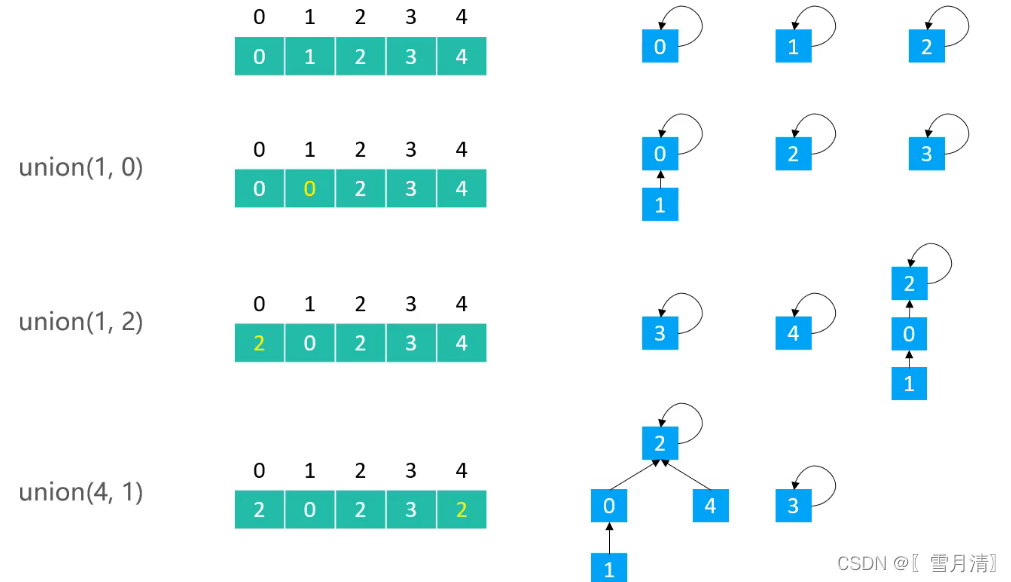
public class UnionFind_QU extends UnionFind {

	public UnionFind_QU(int capacity) {
		super(capacity);

	}

	//查某一个元素的根节点
	@Override
	public int find(int v) {
   //检查下标是否越界
		rangeCheck(v);

  // 一直循环查找节点的根节点
		while (v != parents[v]) {
			v = parents[v];
		}
		return v;
	}

//V1 并到 v2 中
	@Override
	public void union(int v1, int v2) {

		int p1 = find(v1);
		int p2 = find(v2);
		if(p1 == p2) return;
      //将v1 根节点 的 父节点 修改为 v2的根结点 完成合并
		parents[p1] = p2;
	}
}

三、优化

并查集常用快并来实现，但是快并有时会出现树不平衡的情况

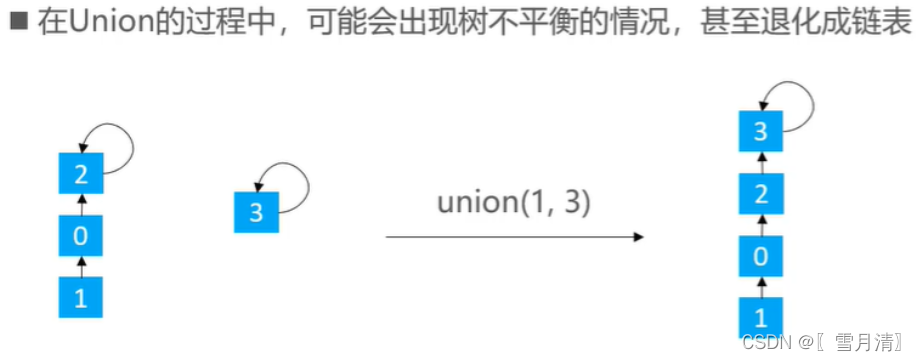
有两种优化思路：rank优化，size优化 

3.1基于size的优化

核心思想：元素少的树 嫁接到 元素多的树

public class UniondFind_QU_S extends UnionFind{

   // 创建sizes 数组记录 以元素（下标）为根结点的元素（节点）个数
	private int[] sizes;

	public UniondFind_QU_S(int capacity) {
		super(capacity);

		sizes = new int[capacity];

   //初始都为 1
		for(int i = 0;i < sizes.length;i++) {
			sizes[i] = 1;
			}

	}

	@Override
	public int find(int v) {

		rangeCheck(v);

		while (v != parents[v]) {
			v = parents[v];
		}
		return v;
	}

	@Override
	public void union(int v1, int v2) {

		int p1 = find(v1);
		int p2 = find(v2);
		if(p1 == p2) return;

		//如果以p1为根结点的元素个数 小于 以p2为根结点的元素个数 p1并到p2上，并且更新p2为根结点的元素个数
	if(sizes[p1] < sizes[p2]) {
		    parents[p1] = p2;
		    sizes[p2] += sizes[p1];

 // 反之 则p2 并到 p1 上，更新p1为根结点的元素个数
	}else {
			parents[p2] = p1;
			sizes[p1] += sizes[p2];
		}
	}
}

基于size优化还有可能会导致树不平衡

3.2基于rank优化

核心思想：矮的树 嫁接到 高的树

public class UnionFind_QU_R extends UnionFind_QU {
   // 创建rank数组  ranks[i] 代表以i为根节点的树的高度
 private int[] ranks;

	public UnionFind_QU_R(int capacity) {
		super(capacity);

		ranks = new int[capacity];

		for(int i = 0;i < ranks.length;i++) {
			ranks[i] = 1;
		}

	}

	public void union(int v1, int v2) {

		int p1 = find(v1);
		int p2 = find(v2);
		if(p1 == p2) return;

    // p1 并到 p2 上 p2为根 树的高度不变
		if(ranks[p1] < ranks[p2]) {
			parents[p1] = p2;

  // p2 并到 p1 上 p1为根 树的高度不变
		} else if(ranks[p1] > ranks[p2]) {
			parents[p2] = p1;

		}else {
    // 高度相同 p1 并到 p2上，p2为根 树的高度+1
			parents[p1] = p2;
			ranks[p2] += 1;
		}
	}
}

基于rank优化，随着Union次数的增多，树的高度依然会越来越高  导致find操作变慢

有三种思路可以继续优化 ：路径压缩、路径分裂、路径减半

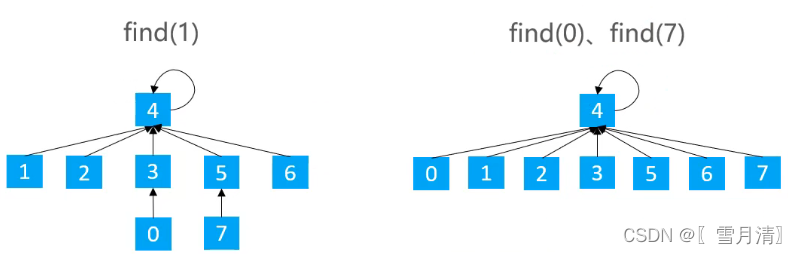
3.2.1路径压缩（Path Compression ）

在find时使路径上的所有节点都指向根节点，从而降低树的高度

/**
 *  Quick Union -基于rank的优化  -路径压缩
 *
 */
public class UnionFind_QU_R_PC extends UnionFind_QU_R {

	public UnionFind_QU_R_PC(int capacity) {
		super(capacity);

	}

	@Override
	public int find(int v) {
		rangeCheck(v);

		if(parents[v] != v) {

        //递归 使得从当前v 到根节点 之间的 所有节点的 父节点都改为根节点
			parents[v] = find(parents[v]);
		}
		return parents[v];
	}
}

虽然能降低树的高度，但是实现成本稍高 

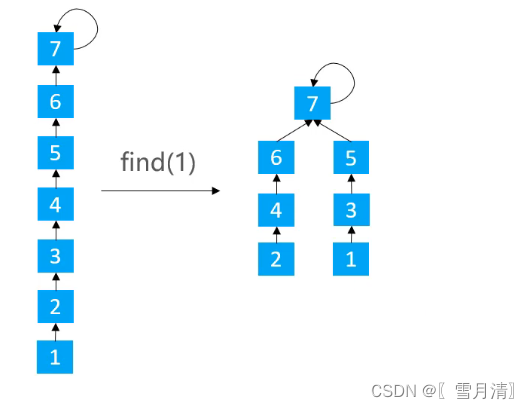
3.2.2路径分裂（Path Spliting）

使路径上的每个节点都指向其祖父节点

/**
 *  Quick Union -基于rank的优化  -路径分裂
 *
 */
public class UnionFind_QU_R_PS extends UnionFind_QU_R {

	public UnionFind_QU_R_PS(int capacity) {
		super(capacity);

	}

	@Override
	public int find(int v) {
		rangeCheck(v);
		while(v != parents[v]) {

			int p = parents[v];
			parents[v] = parents[parents[v]];
			v = p;
		}
		return v;
	}
}

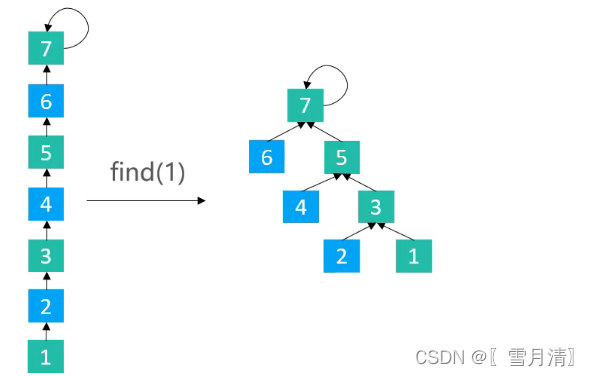
3.2.3路径减半（Path Halving）

使路径上每隔一个节点就指向其祖父节点

/**
 *  Quick Union -基于rank的优化  -路径减半
 *
 */
public class UnionFind_QU_R_PH extends UnionFind_QU_R {

	public UnionFind_QU_R_PH(int capacity) {
		super(capacity);

	}

    public int find(int v) {
    	rangeCheck(v);

		while(v != parents[v]) {
			parents[v] = parents[parents[v]];
			v = parents[v];
		}
		return v;
	}
 }

使用Quick Union + 基于rank的优化 + 路径分裂 或 路径减半

可以保证每个操作的均摊时间复杂度为O(a(n)) , a(n) < 5

到此这篇关于java 数据结构并查集详解的文章就介绍到这了,更多相关java 并查集内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！