C++超详细分析红黑树

目录

• 红黑树
• 红黑树的概念
• 红黑树的性质
• 红黑树结点的定义
• 红黑树的插入操作
• 情况一
• 情况二
• 情况三
• 红黑树的验证
• 用红黑树封装map、set
• 红黑树的迭代器
• 封装map
• 封装set

红黑树

红黑树的概念

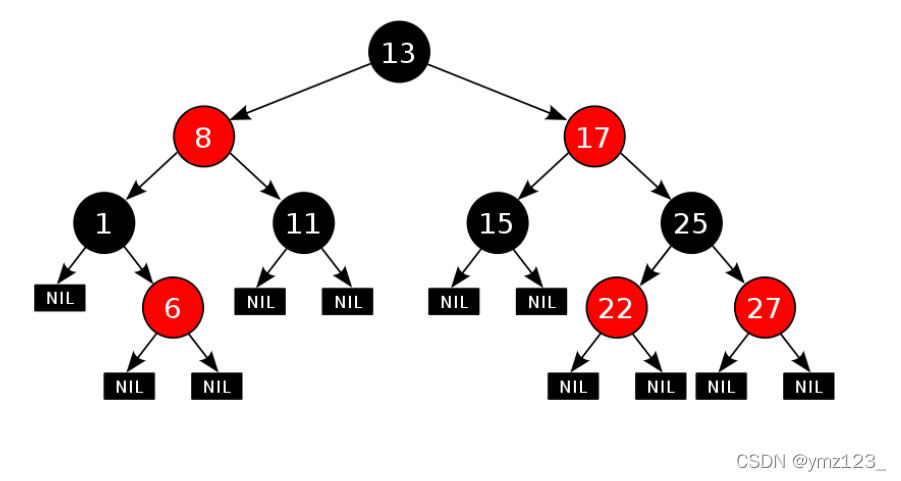
红黑树的概念 红黑树，是一种二叉搜索树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出俩倍，因而是接近平衡的。

红黑树和AVL树都是高效的平衡二叉树，增删改查的时间复杂度都是O()，红黑树不追求绝对平衡，其只需保证最长路径不超过最短路径的2倍，相对而言，降低了插入和旋转的次数，所以在经常进行增删的结构中性能比AVL树更优，而且红黑树实现比较简单，所以实际运用中红黑树更多。

红黑树的性质

• 每个结点不是红色就是黑色
• 根节点是黑色的
• 如果一个结点是红色的，则它的两个孩子结点是黑色的
• 对于每个结点，从该节点到其所有后代叶节点的简单路径上，均包含相同数目的黑色结点
• 每个叶子结点都是黑色的（此处的叶子节点指的是空结点，如上图路径数为11条）

红黑树结点的定义

enum Color {
	BLACK,
	RED
};

template<class T>
struct RBTreeNode
{
	RBTreeNode<T>* _left;
	RBTreeNode<T>* _right;
	RBTreeNode<T>* _parent;

	Color _col;
	T _data;

	RBTreeNode(const T& data)
		: _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _col（RED)
		，_data(data)
	{}
};

红黑树的插入操作

约定：cur为当前节点，p为父节点，g为祖父节点，u为叔叔节点

情况一

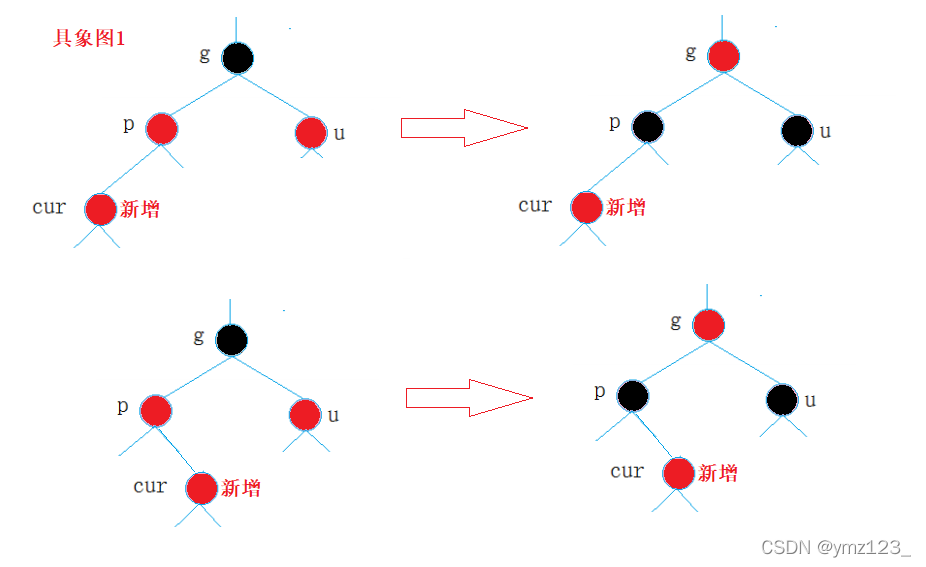
• 情况一：cur为红，p为红，g为黑，u存在且为红注意：此处看到的树，可能是一棵完整的树，也可能是一棵子树
• 解决方式：将p，u改为黑，g改为红，然后把g当成cur，继续向上调整

如果g是根节点，调整完成后，需要将g改为黑色

如果g是子树，g一定有双亲，且g的双亲如果是红色，需要继续向上调整。

情况二

情况二：cur为红，p为红，g为黑，u不存在/u为黑

解决方法：p为g的左孩子，cur为p的左孩子，则进行右单旋；p为g的右孩子，cur为p的右孩子，则进行左单旋。

p变黑，g变红。

1.如果u节点不存在，则cur一定是新插入节点，因为如果cur不是新插入节点，则cur和p一定有一个节点的颜色是黑色，就不满足性质4：每条路径黑色节点个数相同。

2.如果u节点存在，则其一定是黑色的，cur一定不是新增节点，那么cur节点原来的颜色一定是黑色的，是作为子树的祖父，由第一种情况变化过来的

情况三

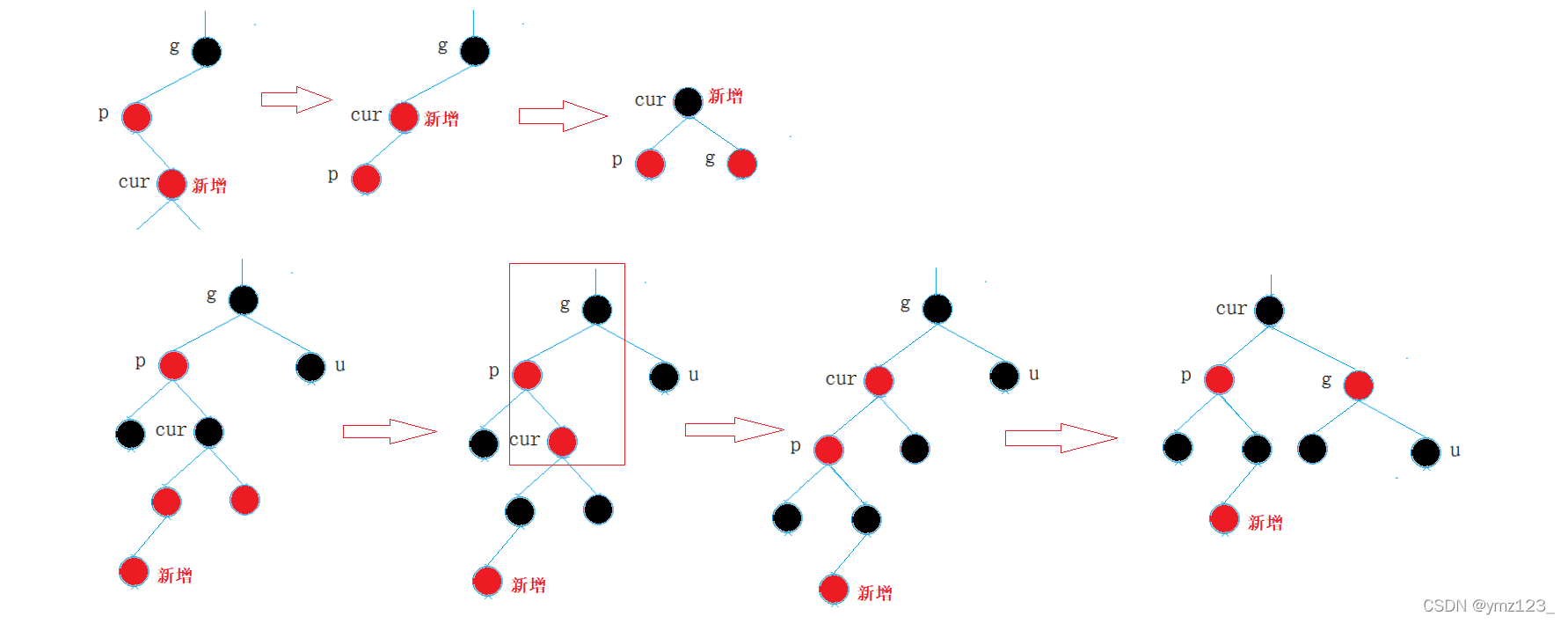
情况三：cur为红，p为红，g为黑，u不存在/u为黑（折线型）

p为g的左孩子，cur为p的右孩子，则针对p做左单旋转；

p为g的右孩子，cur为p的左孩子，则针对p做右单旋转。

即转换为了情况二。再对g做对于旋转。即进行双旋转。

// T->K  set
// T->pair<const K, V> map
template<class K, class T, class KeyOfT>
class RBTree
{
	typedef RBTreeNode<T> Node;
public:
	typedef RBTreeIterator<T, T&, T*> iterator;
	typedef RBTreeIterator<T, const T&, const T*> const_iterator;

	iterator begin();
	iterator end();

	RBTree()
		:_root(nullptr)
	{}

	// 拷贝构造和赋值重载
	// 析构

	Node* Find(const K& key);

	pair<iterator, bool> Insert(const T& data)
	{
		if (_root == nullptr)
		{
			_root = new Node(data);
			_root->_col = BLACK;
			return make_pair(iterator(_root), true);
		}

		Node* parent = nullptr;
		Node* cur = _root;

		KeyOfT kot;
		while (cur)
		{
			if (kot(cur->_data) < kot(data))
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (kot(cur->_data) > kot(data))
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return make_pair(iterator(cur), false);
			}
		}

		// 新增节点，颜色是红色，可能破坏规则3，产生连续红色节点
		cur = new Node(data);
		Node* newnode = cur;
		cur->_col = RED;

		if (kot(parent->_data) < kot(data))
		{
			parent->_right = cur;
			cur->_parent = parent;
		}
		else
		{
			parent->_left = cur;
			cur->_parent = parent;
		}

		// 控制近似平衡
		while (parent && parent->_col == RED)
		{
			Node* grandfather = parent->_parent;
			if (parent == grandfather->_left)
			{
				Node* uncle = grandfather->_right;
				// 情况一：uncle存在且为红，进行变色处理，并继续往上更新处理
				if (uncle && uncle->_col == RED)
				{
					parent->_col = uncle->_col = BLACK;
					grandfather->_col = RED;

					cur = grandfather;
					parent = cur->_parent;
				} // 情况二+三：uncle不存在，或者存在且为黑，需要旋转+变色处理
				else
				{
					// 情况二：单旋+变色
					if (cur == parent->_left)
					{
						RotateR(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;
					}
					else // 情况三：双旋 + 变色
					{
						RotateL(parent);
						RotateR(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					}

					break;
				}
			}
			else  // (parent == grandfather->_right)
			{
				Node* uncle = grandfather->_left;
				if (uncle && uncle->_col == RED)
				{
					parent->_col = uncle->_col = BLACK;
					grandfather->_col = RED;

					cur = grandfather;
					parent = cur->_parent;
				}
				else
				{
					if (parent->_right == cur)
					{
						RotateL(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;
					}
					else
					{
						RotateR(parent);
						RotateL(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					}

					break;
				}
			}
		}

		_root->_col = BLACK;
		return make_pair(iterator(newnode), true);
	}

	void RotateR(Node* parent);
	void RotateL(Node* parent);

private:
	Node* _root;
};

红黑树的验证

红黑树的检测分为两步：

• 检测其是否满足二叉搜索树(中序遍历是否为有序序列)
• 检测其是否满足红黑树的性质

此处用未改造过的红黑树

template<class K, class V>
struct RBTreeNode
{
	RBTreeNode<K, V>* _left;
	RBTreeNode<K, V>* _right;
	RBTreeNode<K, V>* _parent;

	Colour _col;
	pair<K, V> _kv;

	RBTreeNode(const pair<K, V>& kv)
		:_left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _col(RED)
		, _kv(kv)
	{}
};

template<class K, class V>
class RBTree
{
	typedef RBTreeNode<K, V> Node;
public:
	RBTree()
		:_root(nullptr)
	{}

	bool Insert(const pair<K, V>& kv);

	void RotateR(Node* parent);
	void RotateL(Node* parent);

	void _InOrder(Node* root)
	{
		if (root == nullptr)
		{
			return;
		}

		_InOrder(root->_left);
		cout << root->_kv.first << " ";
		_InOrder(root->_right);
	}

	void InOrder()
	{
		_InOrder(_root);
		cout<<endl;
	}

	bool CheckRED_RED(Node* cur)
	{
		if (cur == nullptr)
		{
			return true;
		}

		if (cur->_col == RED && cur->_parent->_col == RED)
		{
			cout << "违反规则三，存在连续的红色节点" << endl;
			return false;
		}

		return CheckRED_RED(cur->_left)
			&& CheckRED_RED(cur->_right);
	}

	// 检查每条路径黑色节点的数量
	bool CheckBlackNum(Node* cur, int blackNum, int benchmark) {
		if (cur == nullptr) {
			if (blackNum != benchmark){
				cout << "违反规则四：黑色节点的数量不相等" << endl;
				return false;}
			return true;
		}

		if (cur->_col == BLACK)
			++blackNum;

		return CheckBlackNum(cur->_left, blackNum, benchmark)
			&& CheckBlackNum(cur->_right, blackNum, benchmark);
	}

	bool IsBalance()
	{
		if (_root == nullptr)
		{
			return true;
		}

		if (_root->_col == RED)
		{
			cout << "根节点是红色，违反规则二" << endl;
			return false;
		}

		// 算出最左路径的黑色节点的数量作为基准值
		int benchmark = 0;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_col == BLACK)
			{
				++benchmark;
			}

			cur = cur->_left;
		}

		int blackNum = 0;
		return CheckRED_RED(_root) && CheckBlackNum(_root, blackNum, benchmark);
	}

private:
	Node* _root;
};

void TestRBTree1()
{
	const int n = 1000000;
	vector<int> a;
	a.reserve(n);
	srand(time(0));
	for (size_t i = 0; i < n; ++i)
	{
		a.push_back(rand());
	}

	RBTree<int, int> t1;
	for (auto e : a)
	{
		t1.Insert(make_pair(e, e));
	}

	cout << t1.IsBalance() << endl;
	//t1.InOrder();
}

用红黑树封装map、set

红黑树的迭代器

begin()与end()

begin()可以放在红黑树中最小节点(即最左侧节点)的位置

end()放在最大节点(最右侧节点)的下一个位置

	typedef RBTreeIterator<T, T&, T*> iterator;
	typedef RBTreeIterator<T, const T&, const T*> const_iterator;

	iterator begin()
	{
		Node* left = _root;
		while (left && left->_left)
		{
			left = left->_left;
		}

		//return left
		return iterator(left);
	}

	iterator end()
	{
		return iterator(nullptr);
	}

操作符重载

template<class T, class Ref, class Ptr>
struct RBTreeIterator
{
	typedef RBTreeNode<T> Node;
	typedef RBTreeIterator<T, Ref, Ptr> Self;
	Node* _node;
	RBTreeIterator(Node* node = nullptr)
		:_node(node)
	{}

	Ref operator*()
	{
		return _node->_data;
	}

	Ptr operator->()
	{
		return &_node->_data;
	}

	Self& operator--()
	{
		// 跟++基本是反过来
		return *this;
	}

	Self& operator++()
	{
		if (_node->_right)
		{
			// 右子树中序第一个节点，也就是右子树的最左节点
			Node* subLeft = _node->_right;
			while (subLeft->_left)
			{
				subLeft = subLeft->_left;
			}

			_node = subLeft;
		}
		else
		{
			// 当前子树已经访问完了，要去找祖先访问，沿着到根节点的路径往上走，
			// 找孩子是父亲左的那个父亲节点
			Node* cur = _node;
			Node* parent = cur->_parent;
			while (parent && parent->_right == cur)
			{
				cur = parent;
				parent = parent->_parent;
			}

			_node = parent;
		}

		return *this;
	}

	bool operator!=(const Self& s) const
	{
		return _node != s._node;
	}

	bool operator==(const Self& s) const
	{
		return _node == s._node;
	}
};

封装map

#pragma once
#include "RBTree.h"

namespace MyMap
{
	template < class K, class V>
	class map
	{
		struct MapKeyOfT
		{
			const K& operator()(const pair<const K, V>& kv)
			{
				return kv.first;
			}
		};
	public:
		typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::iterator iterator;

		iterator begin()
		{
			return _t.begin();
		}

		iterator end()
		{
			return _t.end();
		}

		pair<iterator, bool> insert(const pair<const K, V>& kv)
		{
			return _t.Insert(kv);
		}

		V& operator[](const K& key)
		{
			pair<iterator, bool> ret = _t.Insert(make_pair(key, V()));
			return ret.first->second;
		}
	private:
		RBTree<K, pair<const K, V>, MapKeyOfT> _t;
	};

	void test_map()
	{
		map<string, string> dict;
		dict.insert(make_pair("sort", "排序"));
		dict.insert(make_pair("string", "字符串"));
		dict.insert(make_pair("debug", "找虫子"));
		dict.insert(make_pair("set", "集合"));

		map<string, string>::iterator it = dict.begin();
		while (it != dict.end())
		{
			cout << it->first << ":" << it->second << endl;
			++it;
		}
		cout << endl;
	}
}

封装set

#pragma once
#include "RBTree.h"

namespace MySet
{
	template < class K>
	class set
	{
		struct SetKeyOfT
		{
			const K& operator()(const K& key)
			{
				return key;
			}
		};
	public:
		typedef typename RBTree<K, K, SetKeyOfT>::iterator iterator;

		iterator begin()
		{
			return _t.begin();
		}

		iterator end()
		{
			return _t.end();
		}

		pair<iterator, bool> insert(const K& key)
		{
			return _t.Insert(key);
		}
	private:
		RBTree<K, K, SetKeyOfT> _t;
	};

	void test_set()
	{
		set<int> s;
		s.insert(1);
		s.insert(3);
		s.insert(7);
		s.insert(2);
		s.insert(12);
		s.insert(22);
		s.insert(2);
		s.insert(23);
		s.insert(-2);
		s.insert(-9);
		s.insert(30);

		set<int>::iterator it = s.begin();
		while (it != s.end())
		{
			cout << *it << " ";
			++it;
		}
		cout << endl;

		for (auto e : s)
		{
			cout << e << " ";
		}
		cout << endl;
	}
}

到此这篇关于C++超详细分析红黑树的文章就介绍到这了,更多相关C++ 红黑树内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！