手把手带你用java搞定青蛙跳台阶

目录
  • 问题描述
  • 问题剖析
    • n=1
    • n=2
    • n=3
    • n=4
    • 小结
  • Java代码示例
  • 附：C语言实现青蛙跳台阶
  • 总结

问题描述

一只青蛙一次可以跳上 1 级台阶，也可以跳上2 级。求该青蛙跳上一个n 级的台阶总共有多少种跳法

问题剖析

n=1

此时有一种跳法。

n=2

此时有两种跳法。

n=3

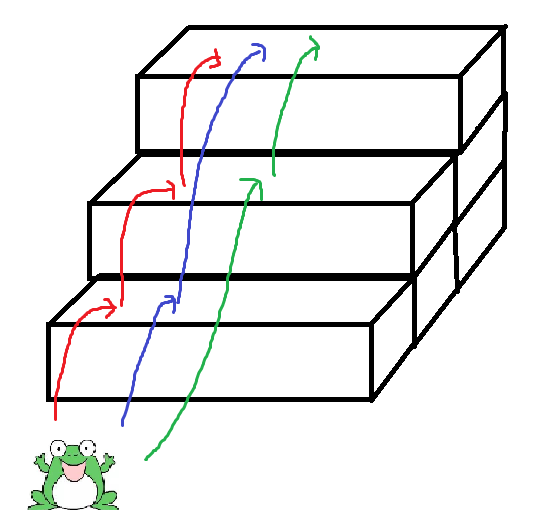
此时有三种跳法。

n=4

此时有五种跳法。

小结

当有n级台阶时，青蛙可以跳1级，也可以跳2级。如果它跳1级，那么还剩下n-1级台阶；如果它跳2级，那么还剩下n-2级台阶。因此n级台阶的跳法等于n-1级台阶跳法加上n-2级台阶跳法之和，也就是：

而如此递归下去，最后n就减到了1和2。

Java代码示例

public static void main(String[] args) {
    Scanner scanner = new Scanner(System.in);
    int n = scanner.nextInt();
    int ret = frogJumping(n);
    System.out.println(ret);
}
public static int frogJumping(int n) {
    if(n == 1) {
        return 1;
    } else if(n == 2) {
        return 2;
    } else {
        return frogJumping(n - 1) + frogJumping(n - 2);
    }
}

例如，当n=5时，结果为：

附：C语言实现青蛙跳台阶

#include<stdio.h>
int FrogJumping(int n)
{
	if (n == 1)
	{
		return 1;
	}
	else if (n == 2)
	{
		return 2;
	}
	else
	{
		return FrogJumping(n - 1) + FrogJumping(n - 2);
	}
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = FrogJumping(n);
	printf("%d级台阶有%d种跳法", n, ret);
	return 0;
}

总结

本篇文章就到这里了，希望能给你带来帮助，也希望您能够多多关注我们的更多内容！

赞 (0)

相关推荐

  • php中青蛙跳台阶的问题解决方法

    一只青蛙一次可以跳上1级台阶,也可以跳上2级.求该青蛙跳上一个n级的台阶总共有多少种跳法(先后次序不同算不同的结果). 思路: 1.找规律 f(1)=1 f(2)=2 f(3)=3 f(4)=5 f(n)=f(n-1)+f(n-2)这是一个斐波那契数列 2.因为调到第n个台阶时,倒数第一个台阶可以一步跳过来,倒数第二个台阶也可以一步就跳过来 非递归版本: JumpFloor(target) if target==1 || target==2 return target jumpSum=0 jum

  • C语言递归之汉诺塔和青蛙跳台阶问题

    C语言递归之汉诺塔和青蛙跳台阶问题

    递归就是一个函数执行过程中调用自己,在c语言中有很多关于递归的经典问题,例如:斐波那契数列问题.汉诺塔问题等,在研究递归问题时我们要注意三点: 1.递归的结束条件 2.递归在每次进行过程中,都得离条件越来越近 3.相邻两次递归调用之间的关联关系 汉诺塔问题: 有三根杆子A, B, C.A杆上有N个(N > 1)穿孔圆盘, 盘的尺寸由下到上依次变小.要求按下列规则将所有圆盘移至C杆: 1.每次只能移动一个圆盘: 2.大盘不能叠在小盘上面,可将圆盘临时置于B杆, 也可将从A杆移出的圆盘重新移回A杆,

  • 一篇文章带你入门java方法

    一篇文章带你入门java方法

    目录 方法的使用 什么是方法 方法的语法 基本语法 代码示例 注意事项 方法的调用 调用规则 代码示例 方法的重载 引例 使用重载 重载规则 方法递归 递归定义 代码示例 递归执行过程分析 总结 方法的使用 什么是方法 初次看到方法两字,心里有些疑惑.方法不是指为获得某种东西或达到某种目的而采取的手段与行为方式吗?这是我们日常生活中所说的方法.而在Java中, 方法就是一个代码片段,类似于C语言中的函数. 方法的存在意义: 1.当代码规模比较复杂的时候,能够模块化地组织代码. 2.做到代码被重复

  • Java青蛙跳台阶问题的解决思路与代码

    Java青蛙跳台阶问题的解决思路与代码

    问题描述 一只青蛙一次可以跳上1级台阶,也可以一次跳上2级台阶,请问跳上n级台阶,该请娃一共有多少种跳法? 解决思路 ①如果只有1级台阶,那显然只有一种跳法. ②如果有2级台阶,那么就有2种跳法,一种是分2次跳.每次跳1级,另一种就是一次跳2级. ③如果台阶级数大于2,设为n的话,这时我们把n级台阶时的跳法看成n的函数,记为,第一次跳的时候有2种不同的选择:一是第一次跳一级,此时跳法的数目等于后面剩下的n-1级台阶的跳法数目,即为,二是第一次跳二级,此时跳法的数目等于后面剩下的n-2级台阶的跳法

  • 手把手带你用java搞定青蛙跳台阶

    手把手带你用java搞定青蛙跳台阶

    目录 问题描述 问题剖析 n=1 n=2 n=3 n=4 小结 Java代码示例 附:C语言实现青蛙跳台阶 总结 问题描述 一只青蛙一次可以跳上 1 级台阶,也可以跳上2 级.求该青蛙跳上一个n 级的台阶总共有多少种跳法 问题剖析 n=1 此时有一种跳法. n=2 此时有两种跳法. n=3 此时有三种跳法. n=4 此时有五种跳法. 小结 当有n级台阶时,青蛙可以跳1级,也可以跳2级.如果它跳1级,那么还剩下n-1级台阶:如果它跳2级,那么还剩下n-2级台阶.因此n级台阶的跳法等于n-1级台阶跳

  • 手把手带你用java搞定汉诺塔

    手把手带你用java搞定汉诺塔

    目录 什么是汉诺塔 问题剖析 n=1 n=2 n=3 小结 Java代码实现 代码讲解 move函数 hanoiTower函数 附:C语言实现汉诺塔 总结 什么是汉诺塔 汉诺塔问题是一个经典的问题.汉诺塔(Hanoi Tower),又称河内塔,源于印度一个古老传说. 大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘. 大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上.并且规定,任何时候,在小圆盘上都不能放大圆盘,且在三根柱子之间一次只能移

  • 手把手带你理解java线程池之工作队列workQueue

    手把手带你理解java线程池之工作队列workQueue

    目录 线程池之工作队列 ArrayBlockingQueue SynchronousQueue LinkedBlockingDeque LinkedBlockingQueue LinkedTransferQueue PriorityBlockingQueue 线程池之工作队列 ArrayBlockingQueue 采用数组来实现,并采用可重入锁ReentrantLock来做并发控制,无论是添加还是读取,都先要获得锁才能进行操作 可看出进行读写操作都使用了ReentrantLock,ArrayBl

  • 学生视角手把手带你写Java 线程池改良版

    目录 Java手写线程池(第二代) 第二代线程池的优化 线程池构造器 线程池拒绝策略 execute方法 手写线程池源码 MyExecutorService MyRejectedExecutionException MyRejectedExecutionHandle 核心类MyThreadPoolExecutor 线程池测试类 Java手写线程池(第二代) 第二代线程池的优化 1:新增了4种拒绝策略.分别为:MyAbortPolicy.MyDiscardPolicy.MyDiscardOldes

  • 学生视角手把手带你写Java 线程池

    目录 Java手写线程池(第一代) 手写线程池-定义参数 手写线程池-构造器 手写线程池-默认构造器 手写线程池-execute方法 手写线程池-处理任务 手写线程池-优雅关闭线程池 手写线程池-暴力关闭线程池 手写线程池-源代码 问题 Java手写线程池(第一代) 经常使用线程池,故今天突发奇想,手写一个线程池,会有很多不足,请多多宽容.因为这也是第一代的版本,后续会更完善. 手写线程池-定义参数 private final AtomicInteger taskcount=new Atomic

  • Java解决青蛙跳台阶问题流程

    Java解决青蛙跳台阶问题流程

    1.问题描述 一只青蛙一次可以跳上1阶台阶,也可以跳上2阶台阶,求该青蛙跳上一个n阶台阶总共有多少种跳法? 2.画图分析  3.问题讲解  一只青蛙,要么1次跳2个台阶,要么1次跳1个台阶. 假设3个台阶为例:如果1次跳1个台阶,那剩下几种跳法?我们来仔细地想一下: 跳了一个台阶之后,剩下的台阶就相当于3 -1个台阶剩下2个台阶,2个台阶的跳法如上图就是2种跳法. 如果一次跳2个台阶,剩下的台阶就相当于3 - 2个台阶剩下1个台阶,1个台阶的跳法如上图是1种跳法.那么加起来就是3种跳法. 所以说

  • C 语言基础实现青蛙跳台阶和汉诺塔问题

    C 语言基础实现青蛙跳台阶和汉诺塔问题

    目录 一.青蛙跳台阶 题目 思路 分析 1. 从跳法次数分析 2. 从过程分析 二.青蛙跳台阶变式1 题目 分析 三.青蛙跳台阶变式2 题目 分析 四.汉诺塔问题(求步数) 题目 思路 分析 五.汉诺塔问题(求移动过程) 题目 思路 分析 一.青蛙跳台阶 题目 一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶.求该青蛙跳上一个 n 级的台阶总共有多少种跳法 思路 遇见题目我们可以在纸上先动手画画,把最简单的几种方式列出来,作比较,找规律. 分析 按照上面表格可以从跳法次数,过程,或者两者结合找规

  • C语言 递归解决青蛙跳台阶问题

    C语言 递归解决青蛙跳台阶问题

    目录 前言 一.求解思路 二.代码实现 1.参考代码 2.运行结果 总结 前言 一只青蛙一次可以跳1级或2级台阶,求当台阶数为n时青蛙有多少种跳法. 一.求解思路 台阶的数量为n. 当 n = 1 时,青蛙有一种跳法,即跳1级台阶. 当 n = 2 时,青蛙有两种跳法,即跳两次1级台阶或跳一次2级台阶. 当 n = 3 时,青蛙可以先跳2级台阶再跳1级台阶,也可以选择先跳1级台阶再跳2级台阶,或者是跳三次1级台阶.依次类推,我们就能知道台阶数为n时青蛙的跳法. 但是,这样子是不是很麻烦呢,再仔细

随机推荐