PyTorch一小时掌握之autograd机制篇

目录

• 概述
• 代码实现
• 手动定义求导
• 计算流量
• 反向传播计算
• 线性回归
• 导包
• 构造 x, y
• 构造模型
• 参数 & 损失函数
• 训练模型
• 完整代码

概述

PyTorch 干的最厉害的一件事情就是帮我们把反向传播全部计算好了.

代码实现

手动定义求导

import torch

# 方法一
x = torch.randn(3, 4, requires_grad=True)

# 方法二
x = torch.randn(3,4)
x.requires_grad = True

b = torch.randn(3, 4, requires_grad=True)
t = x + b
y = t.sum()

print(y)
print(y.backward())
print(b.grad)

print(x.requires_grad)
print(b.requires_grad)
print(t.requires_grad)

输出结果:
tensor(1.1532, grad_fn=<SumBackward0>)
None
tensor([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]])
True
True
True

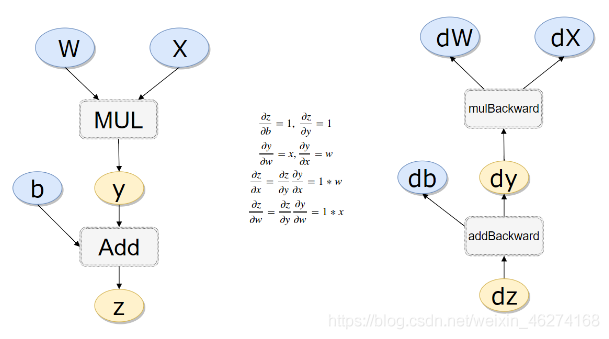
计算流量

# 计算流量
x = torch.rand(1)
w = torch.rand(1, requires_grad=True)
b = torch.rand(1, requires_grad=True)
y = w * x
z = y + b

print(x.requires_grad, w.requires_grad,b.requires_grad, z.requires_grad)
print(x.is_leaf, w.is_leaf, b.is_leaf, y.is_leaf,z.is_leaf)

输出结果:
False True True True
True True True False False

反向传播计算

# 反向传播
z.backward(retain_graph= True)  # 如果不清空会累加起来
print(w.grad)
print(b.grad)

输出结果:
tensor([0.1485])
tensor([1.])

线性回归

导包

import numpy as np
import torch
import torch.nn as nn

构造 x, y

# 构造数据
X_values = [i for i in range(11)]
X_train = np.array(X_values, dtype=np.float32)
X_train = X_train.reshape(-1, 1)
print(X_train.shape)  # (11, 1)

y_values = [2 * i + 1 for i in X_values]
y_train = np.array(y_values, dtype=np.float32)
y_train = y_train.reshape(-1,1)
print(y_train.shape)  # (11, 1)

输出结果:
(11, 1)
(11, 1)

构造模型

# 构造模型
class LinerRegressionModel(nn.Module):
    def __init__(self, input_dim, output_dim):
        super(LinerRegressionModel, self).__init__()
        self.liner = nn.Linear(input_dim, output_dim)

    def forward(self, x):
        out = self.liner(x)
        return out

input_dim = 1
output_dim = 1

model = LinerRegressionModel(input_dim, output_dim)
print(model)

输出结果:
LinerRegressionModel(
(liner): Linear(in_features=1, out_features=1, bias=True)
)

参数 & 损失函数

# 超参数
enpochs = 1000
learning_rate = 0.01

# 损失函数
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)
criterion = nn.MSELoss()

训练模型

# 训练模型
for epoch in range(enpochs):
    # 转成tensor
    inputs = torch.from_numpy(X_train)
    labels = torch.from_numpy(y_train)

    # 梯度每次迭代清零
    optimizer.zero_grad()

    # 前向传播
    outputs = model(inputs)

    # 计算损失
    loss = criterion(outputs, labels)

    # 反向传播
    loss.backward()

    # 更新参数
    optimizer.step()
    if epoch % 50 == 0:
        print("epoch {}, loss {}".format(epoch, loss.item()))

输出结果:
epoch 0, loss 114.47456359863281
epoch 50, loss 0.00021522105089388788
epoch 100, loss 0.00012275540211703628
epoch 150, loss 7.001651829341426e-05
epoch 200, loss 3.9934264350449666e-05
epoch 250, loss 2.2777328922529705e-05
epoch 300, loss 1.2990592040296178e-05
epoch 350, loss 7.409254521917319e-06
epoch 400, loss 4.227155841363128e-06
epoch 450, loss 2.410347860859474e-06
epoch 500, loss 1.3751249525739695e-06
epoch 550, loss 7.844975016269018e-07
epoch 600, loss 4.4756839656656666e-07
epoch 650, loss 2.5517596213830984e-07
epoch 700, loss 1.4577410922811396e-07
epoch 750, loss 8.30393886985803e-08
epoch 800, loss 4.747753479250605e-08
epoch 850, loss 2.709844615367274e-08
epoch 900, loss 1.5436164346738224e-08
epoch 950, loss 8.783858973515635e-09

完整代码

import numpy as np
import torch
import torch.nn as nn

# 构造数据
X_values = [i for i in range(11)]
X_train = np.array(X_values, dtype=np.float32)
X_train = X_train.reshape(-1, 1)
print(X_train.shape)  # (11, 1)

y_values = [2 * i + 1 for i in X_values]
y_train = np.array(y_values, dtype=np.float32)
y_train = y_train.reshape(-1,1)
print(y_train.shape)  # (11, 1)

# 构造模型
class LinerRegressionModel(nn.Module):
    def __init__(self, input_dim, output_dim):
        super(LinerRegressionModel, self).__init__()
        self.liner = nn.Linear(input_dim, output_dim)

    def forward(self, x):
        out = self.liner(x)
        return out

input_dim = 1
output_dim = 1

model = LinerRegressionModel(input_dim, output_dim)
print(model)

# 超参数
enpochs = 1000
learning_rate = 0.01

# 损失函数
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)
criterion = nn.MSELoss()

# 训练模型
for epoch in range(enpochs):
    # 转成tensor
    inputs = torch.from_numpy(X_train)
    labels = torch.from_numpy(y_train)

    # 梯度每次迭代清零
    optimizer.zero_grad()

    # 前向传播
    outputs = model(inputs)

    # 计算损失
    loss = criterion(outputs, labels)

    # 反向传播
    loss.backward()

    # 更新参数
    optimizer.step()
    if epoch % 50 == 0:
        print("epoch {}, loss {}".format(epoch, loss.item()))

到此这篇关于PyTorch一小时掌握之autograd机制篇的文章就介绍到这了,更多相关PyTorch autograd内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！