C#实现优先队列和堆排序

目录

• 优先队列
• 1.API
• 2.初级实现
• 3.堆的定义
• 二叉堆表示法
• 4.堆的算法
• 上浮（由下至上的堆的有序化）
• 下沉（由上至下的堆的有序化）
• 改进
• 堆排序
• 1.堆的构造
• 2.下沉排序
• 先下沉后上浮

优先队列

许多应用程序都需要处理有序的元素，但不一定要求它们全部有序，或是不一定要一次就将它们排序。很多情况下是收集一些元素，处理当前键值最大的元素，然后再收集更多的元素，再处理当前键值最大的元素。这种情况下，需要的数据结构支持两种操作：删除最大的元素和插入元素。这种数据结构类型叫优先队列。

这里，优先队列基于二叉堆数据结构实现，用数组保存元素并按照一定条件排序，以实现对数级别的删除和插入操作。

1.API

优先队列是一种抽象数据类型，它表示了一组值和对这些值的操作，抽象层使应用和实现隔离开来。

2.初级实现

• 1.无序数组实现
  优先队列的 insert 方法和下压栈的 push 方法一样。删除最大元素时，遍历数组找出最大元素，和边界元素交换。
• 2.有序数组实现
  插入元素时，将较大的元素向右移一格（和插入排序一样）。这样删除时，就可以直接 pop。

使用链接也是一样的逻辑。

这些实现总有一种操作需要线性级别的时间复杂度。使用二叉堆可以保证操作在对数级别的时间完成。

3.堆的定义

数据结构二叉堆可以很好地实现优先队列地基本操作。在二叉堆数组中，每个元素都要保证大于等于另两个特定位置地元素。同样，这两个位置地元素又至少要大于等于数组中另外两个元素，以此类推。用二叉树表示：

当一棵二叉树的每个结点都大于等于它的两个子节点时，它被成为堆有序。从任意结点向上，都能得到一列非递减的元素；从任意结点向下，都能得到一列非递增的元素。根结点是堆有序的二叉树中最大的结点。

二叉堆表示法

这里使用完全二叉树表示：将二叉树的结点按照层级顺序（从上到下，从左往右）放入数组中，不使用数组的第一个位置（为了方便计算），根结点在位置 1 ，它的子结点在位置 2 和 3，子结点的子结点分别在位置 4，5，6，7，一次类推。

在一个二叉堆中，位置 k 的结点的父节点位置在 k/2，而它的两个子结点在 2k 和 2k + 1。可以通过计算数组的索引而不是指针就可以在树中上下移动。

一棵大小为 N 的完全二叉树的高度为 lgN。

4.堆的算法

用长度为 N+1 的私有数组 pq[ ] 表示一个大小为 N 的堆。

堆在进行插入或删除操作时，会打破堆的状态，需要遍历堆并按照要求将堆的状态恢复。这个过程称为 堆的有序化。

堆的有序化分为两种情况：当某个结点的优先级上升（或在堆底加入一个新的元素）时，需要由下至上恢复堆的顺序；当某个结点的优先级下降（例如将根节点替换为一个较小的元素），需要由上至下恢复堆的顺序。

上浮（由下至上的堆的有序化）

当某个结点比它的父结点更大时，交换它和它的父节点，这个结点交换到它父节点的位置。但有可能比它现在的父节点大，需要继续上浮，直到遇到比它大的父节点。（这里不需要比较这个子结点和同级的另一个子结点，因为另一个子结点比它们的父结点小）

        //上浮
        private void Swim(int n)
        {
            while (n > 1 && Less(n / 2, n))
            {
                Exch(n/2,n);
                n = n / 2;
            }
        }

下沉（由上至下的堆的有序化）

当某个结点 k 变得比它的两个子结点（2k 和 2k+1）更小时，可以通过将它和它的两个子结点较大者交换来恢复堆有序。交换后在子结点处可能继续打破堆有序，需要继续重复下沉，直到它的子结点都比它小或到达底部。

        //下沉
        private void Sink(int k)
        {
            while (2 * k <= N)
            {
                int j = 2 * k;
                //取最大的子节点
                if (j < N && Less(j, j + 1))
                    j++;

                //如果父节点不小子节点，退出循环
                if (!Less(k,j))
                    break;

                //否则交换，继续下沉
                Exch(j,k);
                k = j;
            }
        }

知道了上浮和下沉的逻辑，就可以很好理解在二叉堆中插入和删除元素的逻辑。

插入元素：将新元素加到数组末尾，增加堆的大小并让这个新元素上浮到合适的位置。

删除最大元素：从数组顶端（即 pq[1]）删除最大元素，并将数组最后一个元素放到顶端，减少数组大小并让这个元素下沉到合适位置。

    public class MaxPriorityQueue
    {
        private IComparable[] pq;
        public int N;
        public MaxPriorityQueue(int maxN)
        {
            pq = new IComparable[maxN+1];
        }

        public bool IsEmpty()
        {
            return N == 0;
        }

        public void Insert(IComparable value)
        {
            pq[++N] = value;
            Swim(N);
        }

        public IComparable DeleteMax()
        {
            IComparable max = pq[1];
            Exch(1,N--);
            pq[N + 1] = null;
            Sink(1);
            return max;
        }

        //下沉
        private void Sink(int k)
        {
            while (2 * k <= N)
            {
                int j = 2 * k;
                //取最大的子节点
                if (j < N && Less(j, j + 1))
                    j++;

                //如果父节点不小子节点，退出循环
                if (!Less(k,j))
                    break;

                //否则交换，继续下沉
                Exch(j,k);
                k = j;
            }
        }

        //上浮
        private void Swim(int n)
        {
            while (n > 1 && Less(n / 2, n))
            {
                Exch(n/2,n);
                n = n / 2;
            }
        }

        private void Exch(int i, int j)
        {
            IComparable temp = pq[i];
            pq[i] = pq[j];
            pq[j] = temp;
        }

        private bool Less(int i, int j)
        {
            return pq[i].CompareTo(pq[j]) < 0;
        }
    }

上述算法对优先队列的实现能够保证插入和删除最大元素这两个操作的用时和队列的大小成对数关系。这里省略了动态调整数组大小的代码，可以参考下压栈。

对于一个含有 N 个元素的基于堆的优先队列，插入元素操作只需要不超过（lgN + 1）次比较，因为 N 可能不是 2 的幂。删除最大元素的操作需要不超过 2lgN次比较（两个子结点的比较和父结点与较大子节点的比较）。

对于需要大量混杂插入和删除最大元素的操作，优先队列很适合。

改进

• 1.多叉堆
  基于数组表示的完全三叉树：对于数组 1 至 N 的 N 个元素，位置 k 的结点大于等于位于 3k-1, 3k ,3k +1 的结点，小于等于位于 （k+1）/ 3 的结点。
• 2.调整数组大小
  使用动态数组，可以构造一个无需关注队列大小的优先队列。可以参考下压栈。
• 3.索引优先队列
  在许多应用程序中，允许客户端引用优先级队列中已经存在的项目是有意义的。一种简单的方法是将唯一的整数索引与每个项目相关联。

堆排序

我们可以把任意优先队列变成一种排序方法：先将所有元素插入一个查找最小元素的优先队列，再重复调用删除操作删除最小元素来将它们按顺序删除。这种排序成为堆排序。

堆排序的第一步是堆的构造，第二步是下沉排序阶段。

1.堆的构造

简单的方法是利用前面优先队列插入元素的方法，从左到右遍历数组调用Swim 方法（由上算法所需时间和 N logN 成正比）。一个更聪明高效的方法是，从右（中间位置）到左调用Sink 方法，只需遍历一半数组，因为另一半是大小为 1 的堆。这种方法只需少于 2N 次比较和 少于 N 次交换。（堆的构造过程中处理的堆都比较小。例如，要构造一个 127 个元素的数组，需要处理 32 个大小为 3 的堆， 16 个大小为 7 的堆，8 个大小为 15 的堆， 4 个大小为 31 的堆， 2 个大小为 63 的堆和 1 个大小为127的堆，因此在最坏情况下，需要 32*1 + 16*2 + 8*3 + 4*4 + 2*5 + 1*6 = 120 次交换，以及两倍的比较）。

2.下沉排序

堆排序的主要工作在第二阶段。将堆中最大元素和堆底元素交换，并下沉至 N--。相当于删除最大元素并将堆底元素放至堆顶（优先队列删除操作），将删除的最大元素放入空出的数组位置。

    public class MaxPriorityQueueSort
    {
        public static void Sort(IComparable[] pq)
        {
            int n = pq.Length;

            for (var k = n / 2; k >= 1; k--)
            {
                Sink(pq, k, n);
            }

            //上浮需要遍历全部
            //for (var k = n; k >= 1; k--)
            //{
            //    Swim(pq, k);
            //}

            while (n > 1)
            {
                Exch(pq,1,n--);
                Sink(pq,1,n);
            }
        }

        private static void Swim(IComparable[] pq, int n)
        {
            while (n > 1 && Less(pq,n / 2, n))
            {
                Exch(pq,n / 2, n);
                n = n / 2;
            }
        }

        //下沉
        private static void Sink(IComparable[] pq,int k, int N)
        {
            while (2 * k <= N)
            {
                int j = 2 * k;
                //取最大的子节点
                if (j < N && Less(pq,j, j + 1))
                    j++;

                //如果父节点不小子节点，退出循环
                if (!Less(pq, k,j))
                    break;

                //否则交换，继续下沉
                Exch(pq, j,k);
                k = j;
            }
        }

        private static void Exch(IComparable[] pq, int i, int j)
        {
            IComparable temp = pq[i-1];
            pq[i - 1] = pq[j - 1];
            pq[j - 1] = temp;
        }

        private static bool Less(IComparable[] pq, int i, int j)
        {
            return pq[i - 1].CompareTo(pq[j - 1]) < 0;
        }

        public static void Show(IComparable[] a)
        {
            for (var i = 0; i < a.Length; i++)
                Console.WriteLine(a[i]);
        }
    }

堆排序的轨迹

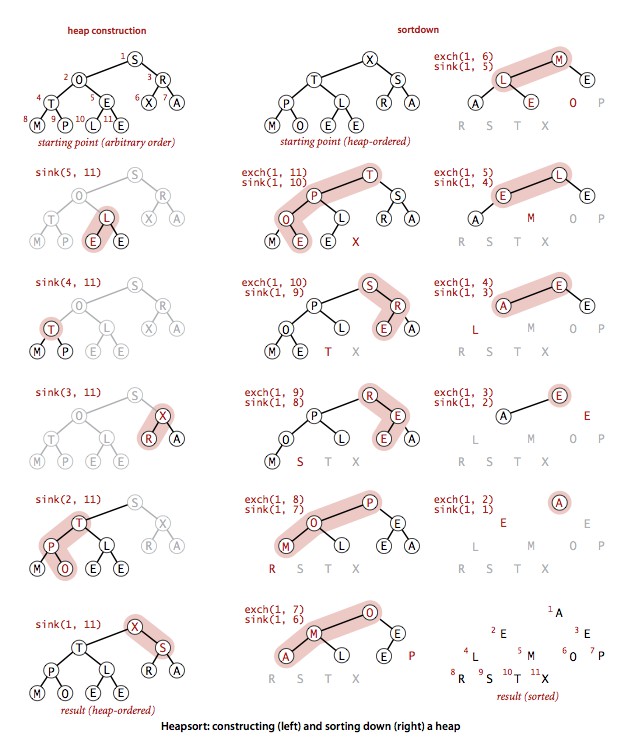
将 N 个元素排序，堆排序只需少于 （2N lgN + 2N）次比较以及一半次数的交换。2N 来自堆的构造，2N lgN 是每次下沉操作最多需要 2lgN 次比较。

先下沉后上浮

在排序过程中，大多数重新插入堆中的项目都会一直到达底部。因此，通过避免检查元素是否已到达其位置，可以简单地提升两个子结点中的较大者直到到达底部，然后上浮到适当位置，从而节省时间。这个方法将比较数减少了2倍，但需要额外的簿空间。只有当比较操作代价较高时可以使用这种方法。（例如将字符串或其他键值较长类型的元素排序）。

堆排序是能够同时最优利用空间和时间的方法，在最坏情况下也能保证 ~2N lgN 次比较和恒定的额外空间。当空间紧张时，可以使用堆排序。但堆排序无法利用缓存。因为它的数组元素很少喝相邻的其他元素比较，因此缓存未命中的次数要远高于大多数比较都在相邻元素之间进行的算法。

到此这篇关于C#实现优先队列和堆排序的文章就介绍到这了。希望对大家的学习有所帮助，也希望大家多多支持我们。