关于PyTorch 自动求导机制详解

自动求导机制

从后向中排除子图

每个变量都有两个标志：requires_grad和volatile。它们都允许从梯度计算中精细地排除子图，并可以提高效率。

requires_grad

如果有一个单一的输入操作需要梯度，它的输出也需要梯度。相反，只有所有输入都不需要梯度，输出才不需要。如果其中所有的变量都不需要梯度进行，后向计算不会在子图中执行。

>>> x = Variable(torch.randn(5, 5))
>>> y = Variable(torch.randn(5, 5))
>>> z = Variable(torch.randn(5, 5), requires_grad=True)
>>> a = x + y
>>> a.requires_grad
False
>>> b = a + z
>>> b.requires_grad
True

这个标志特别有用，当您想要冻结部分模型时，或者您事先知道不会使用某些参数的梯度。

autograd是专门为了BP算法设计的，所以这autograd只对输出值为标量的有用，因为损失函数的输出是一个标量。如果y是一个向量，那么backward()函数就会失效。

model = torchvision.models.resnet18(pretrained=True)
for param in model.parameters():
  param.requires_grad = False
# Replace the last fully-connected layer
# Parameters of newly constructed modules have requires_grad=True by default
model.fc = nn.Linear(512, 100)

# Optimize only the classifier
optimizer = optim.SGD(model.fc.parameters(), lr=1e-2, momentum=0.9)

上面的optim.SGD()只需要传入需要优化的参数即可。

volatile

纯粹的inference模式(可以理解为只需要进行前向)下推荐使用volatile，当你确定你甚至不会调用.backward()时。它比任何其他自动求导的设置更有效——它将使用绝对最小的内存来评估模型。volatile也决定了require_grad is False。

volatile不同于require_grad的传递。如果一个操作甚至只有有一个volatile的输入，它的输出也将是volatile。Volatility比“不需要梯度”更容易传递——只需要一个volatile的输入即可得到一个volatile的输出，相对的，需要所有的输入“不需要梯度”才能得到不需要梯度的输出。使用volatile标志，您不需要更改模型参数的任何设置来用于inference。创建一个volatile的输入就够了，这将保证不会保存中间状态。

>>> regular_input = Variable(torch.randn(5, 5))
>>> volatile_input = Variable(torch.randn(5, 5), volatile=True)
>>> model = torchvision.models.resnet18(pretrained=True)
>>> model(regular_input).requires_grad
True
>>> model(volatile_input).requires_grad
False
>>> model(volatile_input).volatile
True
>>> model(volatile_input).creator is None
True

自动求导如何编码历史信息

每个变量都有一个.creator属性，它指向把它作为输出的函数。这是一个由Function对象作为节点组成的有向无环图（DAG）的入口点，它们之间的引用就是图的边。每次执行一个操作时，一个表示它的新Function就被实例化，它的forward()方法被调用，并且它输出的Variable的创建者被设置为这个Function。然后，通过跟踪从任何变量到叶节点的路径，可以重建创建数据的操作序列，并自动计算梯度。

variable和function它们是彼此不分开的，先上图：

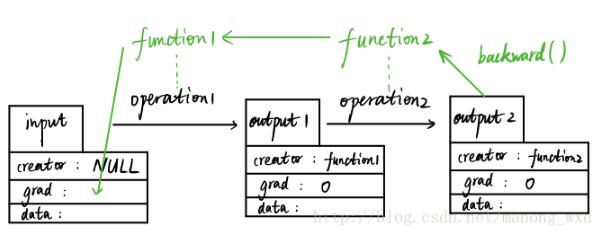
如图，假设我们有一个输入变量input（数据类型为Variable）input是用户输入的，所以其创造者creator为null值，input经过第一个数据操作operation1（比如加减乘除运算）得到output1变量（数据类型仍为Variable），这个过程中会自动生成一个function1的变量（数据类型为Function的一个实例），而output1的创造者就是这个function1。随后，output1再经过一个数据操作生成output2，这个过程也会生成另外一个实例function2，output2的创造者creator为function2。

在这个向前传播的过程中，function1和function2记录了数据input的所有操作历史，当output2运行其backward函数时，会使得function2和function1自动反向计算input的导数值并存储在grad属性中。

creator为null的变量才能被返回导数，比如input，若把整个操作流看成是一张图（Graph）,那么像input这种creator为null的被称之为图的叶子（graph leaf）。而creator非null的变量比如output1和output2，是不能被返回导数的，它们的grad均为0。所以只有叶子节点才能被autograd。

>>> from torch.autograd import Variable
>>> import torch
>>> x = Variable(torch.ones(2), requires_grad = >>> True)
>>> z=4*x*x
>>> y=z.norm()
>>> y
Variable containing:
 5.6569
[torch.FloatTensor of size 1]
>>> y.backward()
>>> x.grad
Variable containing:
 5.6569
 5.6569
[torch.FloatTensor of size 2]
>>> z.grad

>>> y.grad

Variable上的In-place操作

in-place计算，类似'+='运算，表示内部直接替换，in-place操作都使用_作为后缀。例如，x.copy_(y)

>>> a = torch.Tensor(3,4)
>>> a
 0 0 0 0
 0 0 0 0
 0 0 0 0
[torch.FloatTensor of size 3x4]
>>> a.fill_(2.5)
 2.5000 2.5000 2.5000 2.5000
 2.5000 2.5000 2.5000 2.5000
 2.5000 2.5000 2.5000 2.5000
[torch.FloatTensor of size 3x4]
>>> b = a.add(4.0)
>>> b
 6.5000 6.5000 6.5000 6.5000
 6.5000 6.5000 6.5000 6.5000
 6.5000 6.5000 6.5000 6.5000
[torch.FloatTensor of size 3x4]
>>> a
 2.5000 2.5000 2.5000 2.5000
 2.5000 2.5000 2.5000 2.5000
 2.5000 2.5000 2.5000 2.5000
[torch.FloatTensor of size 3x4]
>>> c = a.add_(4.0)
>>> c
 6.5000 6.5000 6.5000 6.5000
 6.5000 6.5000 6.5000 6.5000
 6.5000 6.5000 6.5000 6.5000
[torch.FloatTensor of size 3x4]
>>> a
 6.5000 6.5000 6.5000 6.5000
 6.5000 6.5000 6.5000 6.5000
 6.5000 6.5000 6.5000 6.5000
[torch.FloatTensor of size 3x4]

在自动求导中支持in-place操作是一件很困难的事情，我们在大多数情况下都不鼓励使用它们。Autograd的缓冲区释放和重用非常高效，并且很少场合下in-place操作能实际上明显降低内存的使用量。除非您在内存压力很大的情况下，否则您可能永远不需要使用它们。

限制in-place操作适用性主要有两个原因：

１．覆盖梯度计算所需的值。这就是为什么变量不支持log_。它的梯度公式需要原始输入，而虽然通过计算反向操作可以重新创建它，但在数值上是不稳定的，并且需要额外的工作，这往往会与使用这些功能的目的相悖。

２．每个in-place操作实际上需要实现重写计算图。不合适的版本只需分配新对象并保留对旧图的引用，而in-place操作则需要将所有输入的creator更改为表示此操作的Function。这就比较棘手，特别是如果有许多变量引用相同的存储（例如通过索引或转置创建的），并且如果被修改输入的存储被任何其他Variable引用，则in-place函数实际上会抛出错误。

In-place正确性检查

每个变量保留有version counter，它每次都会递增，当在任何操作中被使用时。当Function保存任何用于后向的tensor时，还会保存其包含变量的version counter。一旦访问self.saved_tensors，它将被检查，如果它大于保存的值，则会引起错误。

以上这篇关于PyTorch 自动求导机制详解就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持我们。