python树的同构学习笔记

一、题意理解

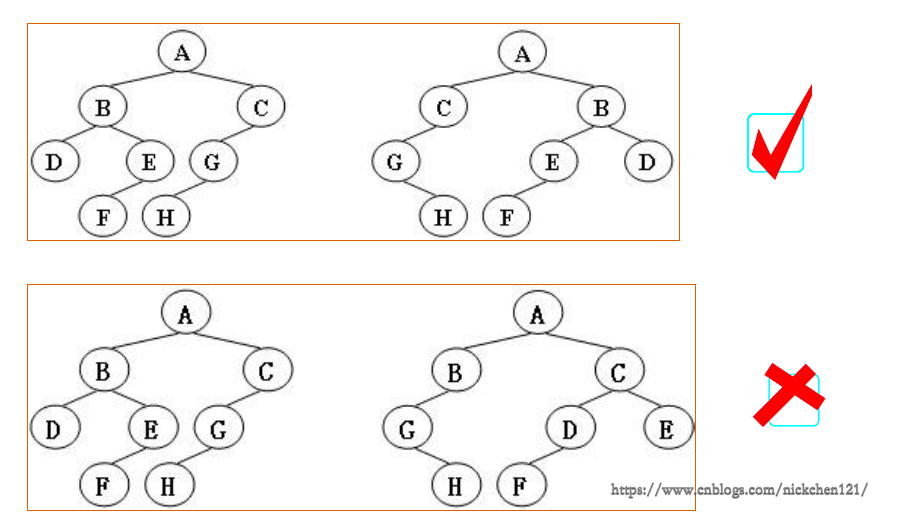
给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2，则我们称两棵树是“同构的”。现给定两棵树，请你判断它们是否是同构的。

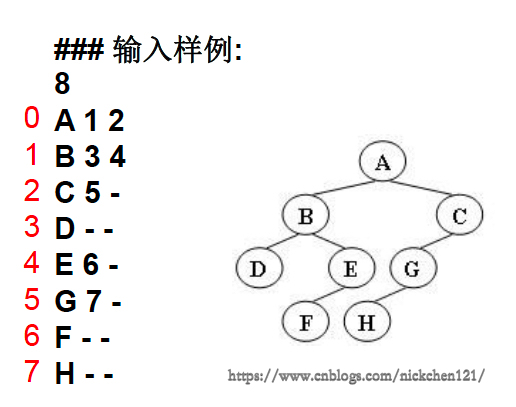
输入格式：输入给出2棵二叉树的信息：

先在一行中给出该树的结点树，随后N行

第i行对应编号第i个结点，给出该结点中存储的字母、其左孩子结点的编号、右孩子结点的编号

如果孩子结点为空，则在相应位置给出“-”

如下图所示，有多种表示的方式，我们列出以下两种：

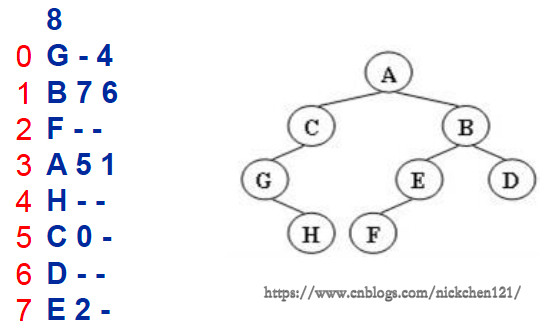
二、求解思路

搜到一篇也是讲这个的，但是那篇并没有完全用到单向链表的方法，所以研究了一下，写了一个是完全用单向链表的方法：

其实应该有更优雅的删除整个单向列表的方法，比如头设为none，可能会改进下？

# python语言实现

L1 = list(map(int, input().split()))
L2 = list(map(int, input().split()))

# 节点
class Node:
  def __init__(self, coef, exp):
    self.coef = coef
    self.exp = exp
    self.next = None

# 单链表
class List:
  def __init__(self, node=None):
    self.__head = node

  # 为了访问私有类
  def gethead(self):
    return self.__head

  def travel(self):
    cur1 = self.__head
    cur2 = self.__head
    if cur1.next != None:
      cur1 = cur1.next
    else:
      print(cur2.coef, cur2.exp, end="")
      return
    while cur1.next != None:
      print(cur2.coef, cur2.exp, end=" ")
      cur1 = cur1.next
      cur2 = cur2.next

    print(cur2.coef, cur2.exp, end=" ")
    cur2 = cur2.next
    print(cur2.coef, cur2.exp, end="")

  # add item in the tail
  def append(self, coef, exp):
    node = Node(coef, exp)
    if self.__head == None:
      self.__head = node
    else:
      cur = self.__head
      while cur.next != None:
        cur = cur.next
      cur.next = node

def addl(l1, l2):
  p1 = l1.gethead()
  p2 = l2.gethead()
  l3 = List()
  while (p1 is not None) & (p2 is not None):
    if (p1.exp > p2.exp):
      l3.append(p1.coef, p1.exp)
      p1 = p1.next
    elif (p1.exp < p2.exp):
      l3.append(p2.coef, p2.exp)
      p2 = p2.next
    else:
      if (p1.coef + p2.coef == 0):
        p1 = p1.next
        p2 = p2.next
      else:
        l3.append(p2.coef + p1.coef, p1.exp)
        p2 = p2.next
        p1 = p1.next
  while p1 is not None:
    l3.append(p1.coef, p1.exp)
    p1 = p1.next
  while p2 is not None:
    l3.append(p2.coef, p2.exp)
    p2 = p2.next
  if l3.gethead() == None:
    l3.append(0, 0)
  return l3

def mull(l1, l2):
  p1 = l1.gethead()
  p2 = l2.gethead()
  l3 = List()
  l4 = List()
  if (p1 is not None) & (p2 is not None):
    while p1 is not None:
      while p2 is not None:
        l4.append(p1.coef * p2.coef, p1.exp + p2.exp)
        p2 = p2.next
      l3 = addl(l3, l4)
      l4 = List()
      p2 = l2.gethead()
      p1 = p1.next
  else:
    l3.append(0, 0)
  return l3

def L2l(L):
  l = List()
  L.pop(0)
  for i in range(0, len(L), 2):
    l.append(L[i], L[i + 1])
  return l

l1 = L2l(L1)
l2 = L2l(L2)
l3 = List()
l3 = mull(l1, l2)
l3.travel()
print("")
l3 = List()
l3 = addl(l1, l2)
l3.travel()

以上就是本次介绍的全部内容知识点，相关内容可以参阅下方知识点，感谢大家对我们的支持。