C++使用string的大数快速模幂运算（6）

本次项目目标：使用C++完成对于大数的相关运算，具体有加减乘除取模。

项目要点

1.大数指的是远超long long int的数据

2.将大数用矩阵进行存储，并通过矩阵实现运算

3.本人采用字符串进行存储，应注意char的特点

比如：char a=161；

cout<<(int)a;

此时会输出-95，而不是161，char类型首个比特位是作为正负号的

模幂快速算法

a,m为正整数，将m表示为二进制形式

则

可得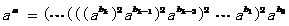

举个例子

代码中有之前的减法 乘法 取模 除法运算

可得以下快速指数算法以及运行截图

#include<iostream>
#include<string>
#include<algorithm>
#include<time.h>
using namespace std;
#define n 10
string dezero(string a)//用来去掉正数前面的0，也就是说可以输入000001类似这样的数字
{
 long int i;
 for(i=0;i<a.length();i++)
 {
 if(a.at(i)>48) break;
 }
 if(i==a.length()) return "0";
 a.erase(0,i);
 return a;
}
int judge(string a,string b)//判断两个正数的大小
{
 if(a.length()>b.length()) return 1;
 if(a.length()<b.length()) return -1;
 long int i;
 for(i=0;i<a.length();i++)
 {
 if(a.at(i)>b.at(i)) return 1;
 if(a.at(i)<b.at(i)) return -1;
 }
 return 0;
}
string minus(string a,string b)//自然数减法
{
 a=dezero(a);
 b=dezero(b);
 long int i,j=0;
 string c="0";
 string c1,c2;
 string d="-";
 if(judge(a,b)==0) return c;
 if(judge(a,b)==1)
 {
 c1=a;
 c2=b;
 }
 if(judge(a,b)==-1)
 {
 c1=b;
 c2=a;
 j=-1;
 }
 reverse(c1.begin(),c1.end());
 reverse(c2.begin(),c2.end());
 for(i=0;i<c2.length();i++)
 {
 if(c2.at(i)>=48&&c2.at(i)<=57) c2.at(i)-=48;
 if(c2.at(i)>=97&&c2.at(i)<=122) c2.at(i)-=87;
 }
 for(i=0;i<c1.length();i++)
 {
 if(c1.at(i)>=48&&c1.at(i)<=57) c1.at(i)-=48;
 if(c1.at(i)>=97&&c1.at(i)<=122) c1.at(i)-=87;
 }
 for(i=0;i<c2.length();i++)
 {
 c1.at(i)=c1.at(i)-c2.at(i);
 }
 for(i=0;i<c1.length()-1;i++)
 {
 if(c1.at(i)<0)
 {
  c1.at(i)+=n;
  c1.at(i+1)--;
 }
 }
 for(i=c1.length()-1;i>=0;i--)
 {
 if(c1.at(i)>0) break;
 }
 c1.erase(i+1,c1.length());
 for(i=0;i<c1.length();i++)
 {
 if(c1.at(i)>=10) c1.at(i)+=87;
 if(c1.at(i)<10) c1.at(i)+=48;
 }
 reverse(c1.begin(),c1.end());
 if(j==-1) c1.insert(0,d);
 return c1;
}
string multiply(string a,string b)//整数
{
 long int i,j,k,yao=0,kai;
 string c1,c2;
 string c3=a+b;
 if(a.at(0)=='-')
 {
 a.erase(0,1);
 yao++;
 }
 if(b.at(0)=='-')
 {
 b.erase(0,1);
 yao++;
 }
 a=dezero(a);
 b=dezero(b);
 if(a.at(0)==48||b.at(0)==48) return "0";
 if(a.length()>b.length())
 {
 c1=a;
 c2=b;
 }
 else
 {
 c1=b;
 c2=a;
 }
 reverse(c1.begin(),c1.end());
 reverse(c2.begin(),c2.end());
 for(i=0;i<c2.length();i++)
 {
 if(c2.at(i)>=48&&c2.at(i)<=57) c2.at(i)-=48;
 if(c2.at(i)>=97&&c2.at(i)<=122) c2.at(i)-=87;
 }
 for(i=0;i<c1.length();i++)
 {
 if(c1.at(i)>=48&&c1.at(i)<=57) c1.at(i)-=48;
 if(c1.at(i)>=97&&c1.at(i)<=122) c1.at(i)-=87;
 }
 for(i=0;i<c3.length();i++) c3.at(i)=0;
 for(i=0;i<c2.length();i++)
 {
 for(j=0;j<c1.length();j++)
 {
  kai=c2.at(i)*c1.at(j);
  c3.at(i+j+1)+=kai/n;
  c3.at(i+j)+=kai%n;
  for(k=i+j;k<c3.length()-1;k++)
  {
  if(c3.at(k)>=n)
  {
   c3.at(k+1)+=c3.at(k)/n;
   c3.at(k)=c3.at(k)%n;
  }
  else
  {
   break;
  }
  }
 }
 }
 for(i=c3.length()-1;i>=0;i--)
 {
 if(c3.at(i)>0) break;
 }
 c3.erase(i+1,c3.length());
 for(i=0;i<c3.length();i++)
 {
 if(c3.at(i)>=10) c3.at(i)+=87;
 if(c3.at(i)<10) c3.at(i)+=48;
 }
 reverse(c3.begin(),c3.end());
 if(yao==1) c3="-"+c3;
 return c3;
}
string mod(string a,string b)
{
 long int i,j=0;
 string c1,c2,c3,d;
 if(a.at(0)=='-') j=1;
 if(judge(a,b)==0) return "0";
 if(judge(a,b)==-1)
 {
 return dezero(a);
 }
 c1=dezero(a);
 c2=dezero(b);
 d="";
 for(i=0;i<c1.length();i++)
 {
 d=d+c1.at(i);
 while(judge(d,b)>=0)
 {
  d=minus(d,b);
  d=dezero(d);
 }
 }
 if(j==1) d=minus(b,d);
 return dezero(d);
}
string divide(string a,string b)//正整数除法
{
 if(b.length()==1&&b.at(0)==48) return "error";
 long int i,j;
 string c1,c2,d,e;
 if(judge(a,b)==0) return "1";
 if(judge(a,b)==-1)
 {
 return "0";
 }
 c1=dezero(a);
 c2=dezero(b);
 d="";
 e="";
 for(i=0;i<c1.length();i++)
 {
 j=0;
 d=d+c1.at(i);
 d=dezero(d);
 while(judge(d,b)>=0)
 {
  d=minus(d,b);
  d=dezero(d);
  j++;
 }
 e=e+"0";
 e.at(i)=j;
 }
 for(i=0;i<e.length();i++)
 {
 if(e.at(i)>=10) e.at(i)+=87;
 if(e.at(i)<10) e.at(i)+=48;
 }
 e=dezero(e);
 return e;
}
string quickpower(string a,string b,string c)//快速指数算法a的b次方mod c
{
 //进制转换
 string e;
 long int i;
 i=0;
 while(1)
 {
 if(b.length()==1&&b.at(0)==48) break;
 e=e+"0";
 e.at(i)=mod(b,"2").at(0);
 b=divide(b,"2");
 i++;
 }
 reverse(e.begin(),e.end());
 //快速指数算法
 b=e;
 string d="1";
 for(i=0;i<b.length();i++)
 {
 if(b.at(i)==49) d=multiply(d,a);
 if(i!=b.length()-1) d=multiply(d,d);
 d=mod(d,c);
 }
 return d;
}
int main()
{
 string a,b,c;
 while(cin>>a>>b>>c)
 {
 cout<<quickpower(a,b,c)<<endl;
 }
 return 0;
}

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我们。