C++基本算法思想之递推算法思想
递推算法是非常常用的算法思想,在数学计算等场合有着广泛的应用。递推算法适合有明显公式规律的场合。
递推算法基本思想
递推算法是一种理性思维莫斯的代表,根据已有的数据和关系,逐步推到而得到结果。递推算法的执行过程如下:
(1)根据已知结果和关系,求解中间结果。
(2)判断是否达到要求,如果没有达到,则继续根据已知结果和关系求解中间结果。如果满足要求,则表示寻找到一个正确答案。
递推算法需要用户知道答案和问题之间的逻辑关系。在许多数学问题中,都有明确的计算公式可以遵循,因此可以采用递推算法来实现。
递推算法示例
数学里面的斐波那契数列是一个使用递推算法的经典例子。
13世纪意大利数学家斐波那契的《算盘书》中记载了典型的兔子产仔问题,其大意如下:
如果一对一个月大的兔子以后每一个月都可以生一对小兔子,而一对新生的兔子出生两个月才可以生出小兔子。也就是,1月份出生,3月份开始产仔。那么假定一年内没有产生兔子死亡事件,那么1年之后共有多少对兔子呢?
1.递归算法
我们来分析一下兔子产仔问题。我们先逐月看每月兔子的对数。
第一个月:1对兔子;
第二个月:1对兔子;
第三个月:2对兔子;
第四个月:3对兔子;
第五个月:5对兔子;
第六个月:8对兔子;
………………
从上面可以看出,从第三个月开始,每个月的兔子总对数等于前两个月兔子数的总和。相应的计算公式如下:
第n个月兔子总数Fn=Fn-1+Fn-2。
这里初始第一个月的兔子数F1=1,第二个月的兔子数F2=1。
可以用递归公式来求解。为了通用型的方便,我们可以编写一个算法,用于计算斐波那契数列问题,按照这个思虑来编写相应的兔子产仔问题的求解算法,示例代码如下:
代码如下:
/*
输入参数n为经历的时间(单位是月),程序中通过递归调用来实现斐波那契数列的计算。
*/
int Fibonacci(n)
{
int t1,t2;
if(n>0)
{
if(n==1||n==2)
{
return 1;
}
else
{
t1=Fibonacci(n-1);
t2=Fibonacci(n-2);
return t1+t2;
}
}
else
{
return 0;
}
}
递归算法求解兔子产仔问题
有了上述通过的兔子产仔问题算法后,我们可以求解任意的此类问题。这里给出完整的兔子产仔问题求解代码:
代码如下:
#include<iostream>
using namespace std;
/*
输入参数n为经历的时间(单位是月),程序中通过递归调用来实现斐波那契数列的计算。
*/
int Fibonacci(int n)
{
int t1,t2;
if(n>0)
{
if(n==1||n==2)
{
return 1;
}
else
{
t1=Fibonacci(n-1); //递归调用获取F(n-1)
t2=Fibonacci(n-2); //递归调用获取F(n-2)
return t1+t2;
}
}
else
{
return 0;
}
}
int main()
{
int n,num;
cout<<"递推算法求解兔子产仔问题:"<<endl;
cout<<"请输入时间:"<<endl;
cin>>n;
num=Fibonacci(n);
cout<<"经过"<<n<<"个月之后"<<endl;
cout<<"兔子的数量为:"<<num<<"对"<<endl;
return 0;
}
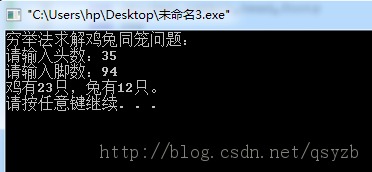
执行该程序,用户输入12,得到如图结果: