java基础二叉搜索树图文详解

目录

• 概念
• 直接实践
• 准备工作：定义一个树节点的类，和二叉搜索树的类。
• 搜索二叉树的查找功能
• 搜索二叉树的插入操作
• 搜索二叉树删除节点的操作-难点
• 性能分析
• 总程序-模拟实现二叉搜索树
• 和java类集的关系
• 总结

概念

二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树：
1、若它的左子树不为空，则左子树上所有节点的值都小于根结点的值。
2、若它的右子树不为空，则右子树上所有节点的值都大于根结点的值。
3、它的左右子树也分别为二叉搜索树

直接实践

准备工作：定义一个树节点的类，和二叉搜索树的类。

搜索二叉树的查找功能

假设我们已经构造好了一个这样的二叉树，如下图

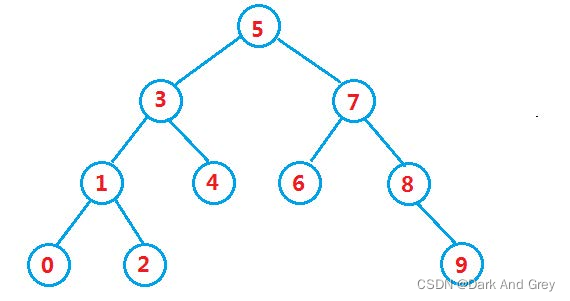
我们要思考的第一个问题是如何查找某个值是否在该二叉树中?

根据上述的逻辑，我们来把搜索的方法进行完善。

搜索二叉树的插入操作

根据上述逻辑，我们来写一个插入节点的代码。

搜索二叉树 删除节点的操作 - 难点

再来分析一下：curDummy 和 parentDummy 是怎么找到“替罪羊”的。

总程序 - 模拟实现二叉搜索树

class TreeNode{
    public int val;
    public TreeNode left;
    public TreeNode right;
    public TreeNode(int val){
        this.val = val;
    }
}

public class BinarySearchTree {
    TreeNode root;

    //在二叉树中 寻找指定 val 值的节点
    // 找到了，返回其节点地址；没找到返回 null
    public TreeNode search(int key){
        TreeNode cur = this.root;
        while(cur != null){
            if(cur.val == key){
                return cur;
            }else if(cur.val < key){
                cur = cur.right;
            }else{
                cur = cur.left;
            }
        }
        return null;
    }
    // 插入操作
    public boolean insert(int key){
        if(this.root == null){
            this.root = new TreeNode(key);
            return true;
        }
        TreeNode cur = this.root;
        TreeNode parent = null;
        while(cur!=null){
            if(key > cur.val){
                parent  = cur;
                cur = cur.right;
            }else if(cur.val == key){
                return false;
            }else{
                parent  = cur;
                cur = cur.left;
            }
        }
        TreeNode node = new TreeNode(key);
        if(parent .val > key){
            parent.left = node;
        }else{
            parent.right = node;
        }
        return true;
    }
    // 删除操作
    public void remove(int key){
        TreeNode cur = root;
        TreeNode parent = null;
        // 寻找 删除节点位置。
        while(cur!=null){
            if(cur.val == key){
                removeNode(cur,parent);// 真正删除节点的代码
                break;
            }else if(cur.val < key){
                parent = cur;
                cur = cur.right;
            }else{
                parent = cur;
                cur = cur.left;
            }
        }
    }
    // 辅助删除方法：真正删除节点的代码
    private void removeNode(TreeNode cur,TreeNode parent){
        // 情况一
        if(cur.left == null){
            if(cur == this.root){
                this.root = this.root.right;
            }else if( cur == parent.left){
                parent.left = cur.right;
            }else{
                parent.right = cur.right;
            }
            // 情况二
        }else if(cur.right == null){
            if(cur == this.root){
                this.root = root.left;
            }else if(cur == parent.left){
                parent.left = cur.left;
            }else{
                parent.right = cur.left;
            }
            // 情况三
        }else{
            // 第二种方法：在删除节点的右子树中寻找最小值，
            TreeNode parentDummy = cur;
            TreeNode curDummy = cur.right;
            while(curDummy.left != null){
                parentDummy = curDummy;
                curDummy = curDummy.left;
            }
            // 此时 curDummy 指向的 cur 右子树
            cur.val = curDummy.val;
            if(parentDummy.left != curDummy){
                parentDummy.right = curDummy.right;
            }else{
                parentDummy.left = curDummy.right;
            }

        }
    }
   // 中序遍历
    public void inorder(TreeNode root){
        if(root == null){
            return;
        }
        inorder(root.left);
        System.out.print(root.val+" ");
        inorder(root.right);
    }

    public static void main(String[] args) {
        int[] array = {10,8,19,3,9,4,7};
        BinarySearchTree binarySearchTree = new BinarySearchTree();
        for (int i = 0; i < array.length; i++) {
            binarySearchTree.insert(array[i]);
        }
        binarySearchTree.inorder(binarySearchTree.root);
        System.out.println();// 换行
        System.out.print("插入重复的数据 9：" + binarySearchTree.insert(9));
        System.out.println();// 换行
        System.out.print("插入不重复的数据 1：" + binarySearchTree.insert(1));
        System.out.println();// 换行
        binarySearchTree.inorder(binarySearchTree.root);
        System.out.println();// 换行
        binarySearchTree.remove(19);
        System.out.print("删除元素 19 ：");
        binarySearchTree.inorder(binarySearchTree.root);
        System.out.println();// 换行
        System.out.print("查找不存在的数据50 ：");
        System.out.println(binarySearchTree.search(50));
        System.out.print("查找存在的数据 7：");
        System.out.println(binarySearchTree.search(7));
    }
}

性能分析

  插入和删除操作都必须先查找，查找效率代表了二叉搜索树中各个操作的性能。
 
  对有n个结点的二叉搜索树，若每个元素查找的概率相等，则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数，即结点越深，则比较次数越多。
 
  但对于同一个关键码集合，如果各关键码插入的次序不同，可能得到不同结构的二叉搜索树：

如果我们能保证 二叉搜索树的左右子树高度差不超过1。尽量满足高度平衡条件。
这就成 AVL 树了（高度平衡的二叉搜索树）。而AVL树，也有缺点：需要一个频繁的旋转。浪费很多效率。
至此 红黑树就诞生了，避免更多的旋转。

和 java 类集的关系

TreeMap 和 TreeSet 即 java 中利用搜索树实现的 Map 和 Set；实际上用的是红黑树，而红黑树是一棵近似平衡的二叉搜索树，即在二叉搜索树的基础之上 + 颜色以及红黑树性质验证，关于红黑树的内容，等博主学了，会写博客的。

总结

到此这篇关于java基础二叉搜索树的文章就介绍到这了,更多相关java二叉搜索树内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！