C语言取模取整的深入理解

目录

• 一：四大取整
• 1.1、 0向取整
• 1.2、  -∞取整（ 地板取整）
• 1.3、 +∞取整
• 1.4、 四舍五入取整
• 1.5、 例子汇总
• 二：取模 / 取余
• 2.1、 概念
• 2.2、 示例（C和Python）
• 2.3、 取余和取模一样吗？
• 2.4、 计算数据同符号
• 2.5、 计算数据不同符号
• 2.6、 总结

一：四大取整

1.1、 0向取整

看代码：

#include <stdio.h>
int main()
{
	//本质是向0取整
	int i = -2.9;
	int j = 2.9;
	printf("%d\n", i); //结果是：-2
	printf("%d\n", j); //结果是：2
    printf("%d %d\n", 5 / 2, -5 / 2);  // 2 -2
	return 0;
}

C中默认0向取整，画图解释0向取整：

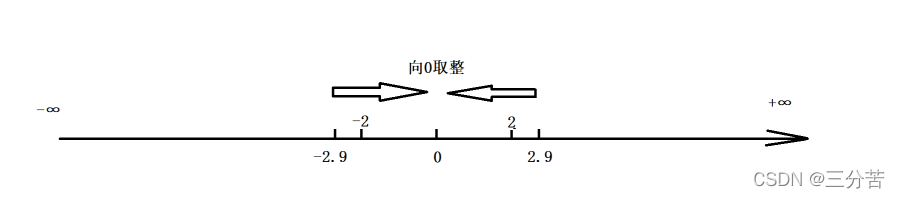
C语言当中有一个trunc函数，运用的也是0向取整。注意引用头文件#include<math.h>.示例如下：

#include <stdio.h>
#include<math.h>
int main()
{
	int i = -2.9;
	int j = 2.9;
	printf("%d\n", i); //结果是：-2
	printf("%d\n", j); //结果是：2
	printf("%d\n", (int)trunc(2.9)); //结果是：2 //结果是：-2
	printf("%d\n", (int)trunc(-2.9));//结果是：-2
	return 0;
}

1.2、  -∞取整（ 地板取整）

其实运用的是floor函数，跟上述trunc一样引用#include<math.h>

看代码：

#include<stdio.h>
#include<math.h>
int main()
{
	printf("%.1f\n", floor(-2.9)); // -3.0
	printf("%.1f\n", floor(-2.1)); // -3.0
	printf("%.1f\n", floor(2.9));  // 2.0
	printf("%.1f\n", floor(2.1));  // 2.0
	return 0;
}

画图解释-∞取整

1.3、 +∞取整

运用的是ceil函数，同样需要#include<math.h>

看代码：

#include<stdio.h>
#include<math.h>
int main()
{
	printf("%.1f\n", ceil(-2.9));  // -2.0
	printf("%.1f\n", ceil(-2.1));  // -2.0
	printf("%.1f\n", ceil(2.9));   // 3.0
	printf("%.1f\n", ceil(2.1));   // 3.0
	return 0;
}

画图解释+∞取整：

1.4、 四舍五入取整

运用的是round函数，同样需要#include<math.h>

看代码：

#include<stdio.h>
#include<math.h>
int main()
{
	printf("%.1f\n", round(-2.9)); // -3.0
	printf("%.1f\n", round(-2.1)); // -2.0
	printf("%.1f\n", round(2.9));  // 3.0
	printf("%.1f\n", round(2.1));  // 2.0
}

1.5、 例子汇总

#include <stdio.h>
#include <math.h>
int main()
{
	const char* format = "%.1f \t%.1f \t%.1f \t%.1f \t%.1f\n";
	printf("value\tround\tfloor\tceil\ttrunc\n");
	printf("-----\t-----\t-----\t----\t-----\n");
	printf(format, 2.3, round(2.3), floor(2.3), ceil(2.3), trunc(2.3));
	printf(format, 3.8, round(3.8), floor(3.8), ceil(3.8), trunc(3.8));
	printf(format, 5.5, round(5.5), floor(5.5), ceil(5.5), trunc(5.5));
	printf(format, -2.3, round(-2.3), floor(-2.3), ceil(-2.3), trunc(-2.3));
	printf(format, -3.8, round(-3.8), floor(-3.8), ceil(-3.8), trunc(-3.8));
	printf(format, -5.5, round(-5.5), floor(-5.5), ceil(-5.5), trunc(-5.5));
	return 0;
}

 结论：

浮点数（整数/整数），是有很多的取整方式的。

二：取模 / 取余

2.1、 概念

如果a和d是两个自然数，d非零，可以证明存在两个唯一的整数 q 和 r，满足 a = q*d + r 且0 ≤ r < d。其中，q 被称为商，r 被称为余数。

2.2、 示例（C和Python）

#include <stdio.h>
int main()
{
	int a = 10;
	int d = 3;
	printf("%d\n", a % d); //结果是1
	//因为：a=10,d=3,q=3,r=1 0<=r<d(3)
	//所以：a = q*d+r -> 10=3*3+1

	int m = -10;
	int n = 3;
	printf("%d\n", m / n); //C语言中是-3，很好理解
	printf("%d\n", m % n); //C语言是-1

	return 0;
}

在C语言中，我们对-10/3=-3以及-10%3=-1很好理解，没有争议

而在Python中，-10/3竟然=-4，而-10%3竟然=2

为什么呢？

结论：很显然，上面关于取模的定义，并不能满足语言上的取模运算

解析：

因为在C中，现在-10%3出现了负数，根据定义：满足 a = q*d + r 且0 ≤ r < d，C语言中的余数，是不满足定义的， 因为，r<0了。

故，大家对取模有了一个修订版的定义： 如果a和d是两个自然数，d非零，可以证明存在两个唯一的整数 q 和 r，满足 a = q*d + r , q 为整数，且0 ≤ |r| < |d|。其中，q 被称为商，r 被称为余数。

有了这个新的定义，那么C中或者Python中的“取模”，就都能解释了。

解释C: -10 = (-3) * 3 + (-1)

解释Python：-10 = （?）* 3 + 2,其中，可以推到出来,'?'必须是-4(后面验证).即-10 = （-4）* 3 + 2，才能 满足定义。

所以，在不同语言，同一个计算表达式，负数“取模”结果是不同的。我们可以称之为分别叫做正余数 和 负余数

是什么决定了这种现象？

由上面的例子可以看出，具体余数r的大小，本质是取决于商q的。

而商，又取决谁呢？取决于除法计算的时候，取整规则。

2.3、 取余和取模一样吗？

细心的同学，应该看到了，我上面的取模都是带着""的。说明这两个并不能严格等价(虽然大部分情况差不多) 取余或者取模，都应该要算出商，然后才能得出余数。

本质 1 取整：

取余：尽可能让商，进行向0取整。

取模：尽可能让商，向-∞方向取整。

故：

C中%,本质其实是取余。

Python中%，本质其实是取模。

理解链：

对任何一个大于0的数，对其进行0向取整和-∞取整，取整方向是一致的。故取模等价于取余 对任何一个小于0的数，对其进行0向取整和-∞取整，取整方向是相反的。故取模不等价于取余

同符号数据相除，得到的商，一定是正数（正数vs正整数），即大于0！ 故，在对其商进行取整的时候，取模等价于取余。

本质 2 符号：

参与取余的两个数据，如果同符号，取模等价于取余

2.4、 计算数据同符号

看代码：

#include <stdio.h>
int main()
{
	printf("%d\n", 10 / 3);  // 3
	printf("%d\n\n", 10 % 3);// 1
	printf("%d\n", -10 / -3); // 3
	printf("%d\n\n", -10 % -3); // -1
	return 0;
}

在Python中，我们发现运行结果和上述一样。

结论：通过对比试验，更加验证了，参与取余的两个数据，如果同符号，取模等价于取余

2.5、 计算数据不同符号

看代码：

#include <stdio.h>
int main()
{
	printf("%d\n", -10 / 3); //结果：-3
	printf("%d\n\n", -10 % 3); //结果：-1 为什么? -10=(-3)*3+(-1)
	printf("%d\n", 10 / -3); //结果：-3
	printf("%d\n\n", 10 % -3); //结果：1 为什么？10=(-3)*(-3)+1
	return 0;
}

而在Python中，结果却不是这样的。

明显结论：如果不同符号，余数的求法，参考之前定义。而余数符号，与被除数相同。

为什么呢？

重新看看定义：如果a和d是两个自然数，d非零，可以证明存在两个唯一的整数 q 和 r，满足 a = q*d + r , q 为整数，且0 ≤ |r| < |d|。其中，q 被称为商，r 被称为余数

a = q*d + r 变换成 r = a - q*d 变换成 r = a + (-q*d)

对于：x = y + z，这样的表达式，x的符号 与 |y|、|z|中大的数据一致

而r = a + (-q*d)中，|a| 和 |-q*d|的绝对值谁大，取决于商q的取整方式。

c是向0取整的，也就是q本身的绝对值是减小的。如：

-10/3=-3.333.33 向0取整 -3. a=-10 |10|, -q*d=-(-3)*3=9 |9|

10/-3=-3.333.33 向0取整 -3. a=10 |10|, -q*d=-(-3)*(-3)=-9 |9|

绝对值都变小了

python是向-∞取整的，也就是q本身的绝对值是增大的。

-10/3=-3.333.33 '//'向-∞取整 -4. a=-10 |10|, -q*d=-(-4)*3=12 |12|

10/-3=--3.333.33 '//'向-∞取整 -4. a=10 |10|, -q*d=-(-4)*(-3)=-12 |12|

绝对值都变大了

结论：如果参与取余的两个数据符号不同，在C语言中(或者其他采用向0取整的语言如：C++，Java)，余数符号，与被除数 相同。

2.6、 总结

（1）浮点数(或者整数相除)，是有很多的取整方式的。

（2）如果a和d是两个自然数，d非零，可以证明存在两个唯一的整数 q 和 r，满足 a = q*d + r , q 为整数，且0 ≤ |r| < |d|。其中，q 被称为商，r 被称为余数。

（3）在不同语言，同一个计算表达式，“取模”结果是不同的。我们可以称之为分别叫做正余数 和 负余数

（4）具体余数r的大小，本质是取决于商q的。而商，又取决于除法计算的时候，取整规则。

（5）取余vs取模： 取余尽可能让商，进行向0取整。取模尽可能让商，向-∞方向取整。

（6）参与取余的两个数据，如果同符号，取模等价于取余

（7）如果参与取余的两个数据符号不同，在C语言中(或者其他采用向0取整的语言如：         C++，Java)，余数符号，与被 除数相同。（因为采用的向0取整）

到此这篇关于C语言取模取整的深入理解的文章就介绍到这了,更多相关C语言取模取整 内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！