浅谈C++如何求等差素数列

题目

标题：等差素数列

2,3,5,7,11,13,....是素数序列。
类似：7,37,67,97,127,157 这样完全由素数组成的等差数列，叫等差素数数列。
上边的数列公差为30，长度为6。

2004年，格林与华人陶哲轩合作证明了：存在任意长度的素数等差数列。
这是数论领域一项惊人的成果！

有这一理论为基础，请你借助手中的计算机，满怀信心地搜索：

长度为10的等差素数列，其公差最小值是多少？

注意：需要提交的是一个整数，不要填写任何多余的内容和说明文字。

题解

絮絮叨叨（骂骂咧咧

一开始看到这道题还是有点懵的，毕竟我个数学小白，对素数什么的最发怵了。

然后找了好多大佬的题解都没看明白，甚至有一个大佬的代码看的我晕头转向~

然后终于被我找到一份能看懂并且觉得非常正确的代码，思路如下：

思路

两层循环，一层循环用于循环公差，一层循环用于循环起始素数。

需要注意的是，内层循环起始素数的时候，不能无边界循环下去，要设置一个上限，否则外层循环永远无法走到下一个公差（自己写的时候自以为是犯的错

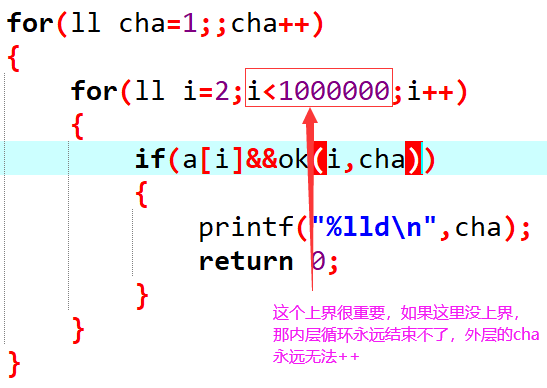
内层循环走的时候，只需要判断：
①这个数是不是素数（作为起始素数最基本的条件）
②判断从这个素数开始，以cha为公差能否存在连续10个等差的素数。【用ok函数来判断的】

如果以上两个条件都满足，则这就是我们要找的长度为10的等差素数列，其公差的最小值

因为我们是从小到大找的，那我们找到的满足条件的第一个就是答案~

#include<stdio.h>
#include<string.h>
#include<math.h>
#include<algorithm>
using namespace std;
typedef long long ll;
const ll maxn=1e6+50;
ll a[maxn];
bool ok(ll n,ll cha)
{
	for(ll i=0;i<10;i++)
	{
		if(!a[n+i*cha])return 0;
	}
	return 1;
}

int main()
{
	a[1]=0;
	a[2]=1;
	a[3]=1;
	for(ll i=4;i<=1000000;i++)
	{
		bool flag=0;
		for(ll j=2;j*j<=i;j++)
		{
			if(i%j==0)
			{
				flag=1;
				break;
			}
		}
		if(flag)a[i]=0;
		else a[i]=1;
	}

	for(ll cha=1;;cha++)
	{
		for(ll i=2;i<1000000;i++)
		{
			if(a[i]&&ok(i,cha))
			{
				printf("%lld\n",cha);
				return 0;
			}
		}
	}
}

后记

其实我对素数一直都怀有敬畏之心，希望能找个时间把素数的相关算法摸摸透，把板子整理齐全~（先给自己挖个坑

要是整理好了，我就把链接更新上来！（咕咕咕~

到此这篇关于浅谈C++如何求等差素数列的文章就介绍到这了,更多相关C++ 等差素数列内容请搜索我们以前的文章或继续浏览下面的相关文章希望大家以后多多支持我们！

赞 (0)

相关推荐

  • C++输出斐波那契数列的两种实现方法

    定义: 斐波那契数列指的是这样一个数列:0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...这个数列从第三项开始,每一项都等于前两项之和. 以输出斐波那契数列的前20项为例: 方法一:比较标准的做法,是借助第三个变量实现的. 复制代码 代码如下: #include<iostream>  using namespace std;int main(){    int f1=0,f2=1,t,n=1;    cout<<"数列第1个

  • C++初始化函数列表详细解析

    在以下三种情况下需要使用初始化成员列表: 一,需要初始化的数据成员是对象的情况: 二,需要初始化const修饰的类成员: 三,需要初始化引用成员数据: 原因:C++可以定义引用类型的成员变量,引用类型的成员变量必须在构造函数的初始化列表中进行初始化.对于类成员是const修饰,或是引用类型的情况,是不允许赋值操作的,(显然嘛,const就是防止被错误赋值的,引用类型必须定义赋值在一起),因此只能用初始化列表对齐进行初始化.成员类型是没有默认构造函数的类.若没有提供显示初始化式,则编译器隐式使用成

  • c++输出斐波那契数列示例分享

    复制代码 代码如下: #include "stdio.h" int Feibo(int Num){if(Num == 1 || Num == 2){return 1;}else{return Feibo(Num - 1) + Feibo(Num - 2);}} void main(){int NumIn,i;scanf("%d", &NumIn);for(i=1;i<NumIn;i++){printf("%d ",Feibo(i))

  • C++求Fib数列

    1. 第一版本程序 int fib(int pos) { int elem = 1; int n1 = 1, n2 = 1; for (int i = 3; i <= pos; i++) { elem = n2 + n1; n1 = n2; n2 = elem; } return elem; } 2. 第二版本 bool fib(int pos, int &elem) { if(pos < 0 || pos > 1024) { elem = 0; return false; }

  • C++项目求Fibonacci数列的参考解答

    C++项目求Fibonacci数列的参考解答

    [项目:求Fibonacci数列] Fibonacci数列在计算科学.经济学等领域中广泛使用,其特点是:第一.二个数是1,从第3个数开始,每个数是其前两个数之和.据此,这个数列为:1 1 2 3 5 8 13 21 34 55 89 --,请设计程序,输出这个数列,直到这个数字超过10000. [提示]数列可以表示为: [参考解答] #include <iostream> using namespace std; int main( ) { int f1,f2,fn,n; f1=f2=1; n

  • 浅谈C++如何求等差素数列

    题目 标题:等差素数列 2,3,5,7,11,13,....是素数序列. 类似:7,37,67,97,127,157 这样完全由素数组成的等差数列,叫等差素数数列. 上边的数列公差为30,长度为6. 2004年,格林与华人陶哲轩合作证明了:存在任意长度的素数等差数列. 这是数论领域一项惊人的成果! 有这一理论为基础,请你借助手中的计算机,满怀信心地搜索: 长度为10的等差素数列,其公差最小值是多少? 注意:需要提交的是一个整数,不要填写任何多余的内容和说明文字. 题解 絮絮叨叨(骂骂咧咧 一开始

  • 浅谈C/C++ 语言中的表达式求值

    经常可以在一些讨论组里看到下面的提问:"谁知道下面C语句给n赋什么值?" m = 1; n = m+++m++; 最近有位不相识的朋友发email给我,问为什么在某个C++系统里,下面表达式打印出两个4,而不是4和5: a = 4; cout << a++ << a; C++ 不是规定 << 操作左结合吗?是C++ 书上写错了,还是这个系统的实现有问题? 注:运行a = 4; cout << a++ << a; 如在Visua

  • 浅谈Java中hashCode的正确求值方法

    本文研究的主要是Java中hashCode的正确求值方法的相关内容,具体如下. 散列表有一项优化,可以将对象的散列码(hashCode)缓存起来,如果散列码不匹配,就不会检查对象的等同性而直接认为成不同的对象.如果散列码(hashCode)相等,才会检测对象是否相等(equals). 如果对象具有相同的散列码(hashCode),他们会被映射到同一个散列桶中.如果散列表中所有对象的散列码(hashCode)都一样,那么该散列表就会退化为链表(linked list),从而大大降低其查询效率. 一

  • 浅谈Pytorch中的自动求导函数backward()所需参数的含义

    正常来说backward( )函数是要传入参数的,一直没弄明白backward需要传入的参数具体含义,但是没关系,生命在与折腾,咱们来折腾一下,嘿嘿. 对标量自动求导 首先,如果out.backward()中的out是一个标量的话(相当于一个神经网络有一个样本,这个样本有两个属性,神经网络有一个输出)那么此时我的backward函数是不需要输入任何参数的. import torch from torch.autograd import Variable a = Variable(torch.Te

  • 浅谈Java实现回溯算法之八皇后问题

    浅谈Java实现回溯算法之八皇后问题

    目录 一.前言 二.浅谈递归 三.回溯算法 四.八皇后问题 五.八皇后变种 六.总结 一.前言 说起八皇后问题,它是一道回溯算法类的经典问题,也可能是我们大部分人在上数据结构或者算法课上遇到过的最难的一道题-- 二.浅谈递归 对于递归算法,我觉得掌握递归是入门数据结构与算法的关键,因为后面学习很多操作涉及到递归,例如链表的一些操作.树的遍历和一些操作.图的dfs.快排.归并排序等等. 递归的实质还是借助栈实现一些操作,利用递归能够完成的操作使用栈都能够完成,并且利用栈的话可以很好的控制停止,效率

  • 浅谈JS运算符&&和|| 及其优先级

    今天看了一段YUI compressor压缩的js代码: userNum && (ind += index,ind >= userNum && (ind -= userNum),ind < 0 && (ind === -2 && (ind = -1),ind += userNum),selLi.removeClass("on"),$(selLi[ind]).addClass("on"));

  • 浅谈javascript运算符——条件,逗号,赋值,()和void运算符

    前面的话 javascript中运算符总共有46个,除了前面已经介绍过的算术运算符.关系运算符.位运算符.逻辑运算符之外,还有很多运算符.本文将介绍条件运算符.逗号运算符.赋值运算符.()和void运算符 条件运算符 条件运算符是javascript中唯一的一个三元运算符(三个操作数),有时直接称做'三元运算符'.通常这个运算符写成'?:',当然在代码中往往不会这么简写,因为这个运算符拥有三个操作数,第一个操作数在'?'之前,第二个操作数在'?'和':'之间,第三个操作数在':'之后 varia

  • 浅谈DOM的操作以及性能优化问题-重绘重排

    浅谈DOM的操作以及性能优化问题-重绘重排

    写在前面: 大家都知道DOM的操作很昂贵. 然后贵在什么地方呢? 一.访问DOM元素 二.修改DOM引起的重绘重排 一.访问DOM 像书上的比喻:把DOM和JavaScript(这里指ECMScript)各自想象为一个岛屿,它们之间用收费桥梁连接,ECMAScript每次访问DOM,都要途径这座桥,并交纳"过桥费",访问DOM的次数越多,费用也就越高.因此,推荐的做法是尽量减少过桥的次数,努力待在ECMAScript岛上.我们不可能不用DOM的接口,那么,怎样才能提高程序的效率? 既然

  • 浅谈DetachedCriteria和Criteria的使用方法(必看)

    在常规的Web编程中,有大量的动态条件查询,即用户在网页上面自由选择某些条件,程序根据用户的选择条件,动态生成SQL语句,进行查询. 比如,我记得在Facebook中可以选择高级查询条件,这个就是个动态的查询了塞,我们无法预知使用多少个查询,直接书写死了在我们的Dao层显然是不服和我们的意思的塞 针对这种需求,对于分层应用程序来说,Web层需要传递一个查询的条件列表给业务层对象,业务层对象获得这个条件列表之后,然后依次取出条件,构造查询语句.这里的一个难点是条件列表用什么来构造?传统上使用Map

  • 浅谈numpy中linspace的用法 (等差数列创建函数)

    浅谈numpy中linspace的用法 (等差数列创建函数)

    linspace 函数 是创建等差数列的函数, 最好是在 Matlab 语言中见到这个函数的,近期在学习Python 中的 Numpy, 发现也有这个函数,以下给出自己在学习过程中的一些总结. (1)指定起始点 和 结束点. 默认 等差数列个数为 50. (2)指定等差数列个数 (3)如果数列的元素个数指定, 可以设置 结束点 状态. endpoint : bool, optional If True, stop is the last sample. Otherwise, it is not

随机推荐