Python数学建模StatsModels统计回归之线性回归示例详解

目录

• 1、背景知识
• 1.1 插值、拟合、回归和预测
• 1.2 线性回归
• 2、Statsmodels 进行线性回归
• 2.1 导入工具包
• 2.2 导入样本数据
• 2.3 建模与拟合
• 2.4 拟合和统计结果的输出
• 3、一元线性回归
• 3.1 一元线性回归 Python 程序：
• 3.2 一元线性回归 程序运行结果：
• 4、多元线性回归
• 4.1 多元线性回归 Python 程序：
• 4.2 多元线性回归 程序运行结果：
• 5、附录：回归结果详细说明

1、背景知识

1.1 插值、拟合、回归和预测

插值、拟合、回归和预测，都是数学建模中经常提到的概念，而且经常会被混为一谈。

• 插值，是在离散数据的基础上补插连续函数，使得这条连续曲线通过全部给定的离散数据点。 插值是离散函数逼近的重要方法，利用它可通过函数在有限个点处的取值状况，估算出函数在其他点处的近似值。
• 拟合，是用一个连续函数（曲线）靠近给定的离散数据，使其与给定的数据相吻合。

因此，插值和拟合都是根据已知数据点求变化规律和特征相似的近似曲线的过程，但是插值要求近似曲线完全经过给定的数据点，而拟合只要求近似曲线在整体上尽可能接近数据点，并反映数据的变化规律和发展趋势。插值可以看作是一种特殊的拟合，是要求误差函数为 0的拟合。由于数据点通常都带有误差，误差为 0 往往意味着过拟合，过拟合模型对于训练集以外的数据的泛化能力是较差的。因此在实践中，插值多用于图像处理，拟合多用于实验数据处理。

• 回归，是研究一组随机变量与另一组随机变量之间关系的统计分析方法，包括建立数学模型并估计模型参数，并检验数学模型的可信度，也包括利用建立的模型和估计的模型参数进行预测或控制。
• 预测是非常广泛的概念，在数模中是指对获得的数据、信息进行定量研究，据此建立与预测目的相适应的数学模型，然后对未来的发展变化进行定量地预测。通常认为，插值和拟合都是预测类的方法。

回归是一种数据分析方法，拟合是一种具体的数据处理方法。拟合侧重于曲线参数寻优，使曲线与数据相符；而回归侧重于研究两个或多个变量之间的关系。

1.2 线性回归

回归分析（Regression analysis)是一种统计分析方法，研究是自变量和因变量之间的定量关系，经常用于预测分析、时间序列模型以及发现变量之间的因果关系。按照变量之间的关系类型，回归分析可以分为线性回归和非线性回归。

线性回归（Linear regression） 假设给定数据集中的目标（y）与特征（X）存在线性关系，即满足一个多元一次方程 。 回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，称为一元线性回归；如果包括两个或多个的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归。
　　
　　根据样本数据，采用最小二乘法可以得到线性回归模型参数的估计量，并使根据估计参数计算的模型数据与给定的样本数据之间误差的平方和为最小。

进一步地，还需要分析对于样本数据究竟能不能采用线性回归方法，或者说线性相关的假设是否合理、线性模型是否具有良好的稳定性？这就需要使用统计分析进行显著性检验，检验因变量与自变量之间的线性关系是否显著，用线性模型来描述它们之间的关系是否恰当。

2、Statsmodels 进行线性回归

本节结合 Statsmodels 统计分析包 的使用介绍线性拟合和回归分析。线性模型可以表达为如下公式：

2.1 导入工具包

import statsmodels.api as sm from statsmodels.sandbox.regression.predstd

import wls_prediction_std

2.2 导入样本数据

样本数据通常保存在数据文件中，因此要读取数据文件获得样本数据。为便于阅读和测试程序，本文使用随机数生成样本数据。读取数据文件导入数据的方法，将在后文介绍。

# 生成样本数据:
nSample = 100
x1 = np.linspace(0, 10, nSample) # 起点为 0，终点为 10，均分为 nSample个点
e = np.random.normal(size=len(x1)) # 正态分布随机数
yTrue = 2.36 + 1.58 * x1 # y = b0 + b1*x1
yTest = yTrue + e # 产生模型数据

本案例是一元线性回归问题，(yTest，x)是导入的样本数据，我们需要通过线性回归获得因变量 y 与自变量 x 之间的定量关系。yTrue 是理想模型的数值，yTest 模拟实验检测的数据，在理想模型上加入了正态分布的随机误差。

2.3 建模与拟合

一元线性回归模型方程为：

　　y = β0 + β1 * x + e

　　先通过 sm.add_constant() 向矩阵 X 添加截距列后，再用 sm.OLS() 建立普通最小二乘模型，最后用 model.fit() 就能实现线性回归模型的拟合，并返回拟合与统计分析的结果摘要。

X = sm.add_constant(x1) # 向 x1 左侧添加截距列 x0=[1,…1]
model = sm.OLS(yTest, X) # 建立最小二乘模型（OLS）
results = model.fit() # 返回模型拟合结果

statsmodels.OLS 是 statsmodels.regression.linear_model 的函数，有 4个参数 (endog, exog, missing, hasconst)。

第一个参数 endog 是回归模型中的因变量 y(t), 是1-d array 数据类型。

第二个输入 exog 是自变量 x0(t),x1(t),…,xm(t)，是(m+1)-d array 数据类型。
　　需要注意的是，statsmodels.OLS 的回归模型没有常数项，其形式为：
　　y = B*X + e = β0*x0 + β1*x1 + e, x0 = [1,…1]
　　而之前导入的数据 (yTest，x1) 并不包含 x0，因此需要在 x1 左侧增加一列截距列 x0=[1,…1]，将自变量矩阵转换为 X = (x0, x1)。函数 sm.add_constant() 实现的就是这个功能。
　　参数 missing 用于数据检查, hasconst 用于检查常量，一般情况不需要。

2.4 拟合和统计结果的输出

Statsmodels 进行线性回归分析的输出结果非常丰富，results.summary() 返回了回归分析的摘要。

print(results.summary()) # 输出回归分析的摘要

摘要所返回的内容非常丰富，这里先讨论最重要的一些结果，在 summary 的中间段落。

==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const          2.4669      0.186     13.230      0.000       2.097       2.837
x1             1.5883      0.032     49.304      0.000       1.524       1.652
==============================================================================

coef：回归系数（Regression coefficient），即模型参数 β0、β1、…的估计值。

std err ：标准差（ Standard deviation），也称标准偏差，是方差的算术平方根，反映样本数据值与回归模型估计值之间的平均差异程度 。标准差越大，回归系数越不可靠。

t：t 统计量（t-Statistic），等于回归系数除以标准差，用于对每个回归系数分别进行检验，检验每个自变量对因变量的影响是否显著。如果某个自变量 xi的影响不显著，意味着可以从模型中剔除这个自变量。

P>|t|：t检验的 P值（Prob(t-Statistic)），反映每个自变量 xi 与因变量 y 的相关性假设的显著性。如果 p<0.05，可以理解为在0.05的显著性水平下变量xi与y存在回归关系，具有显著性。

[0.025,0.975]：回归系数的置信区间（Confidence interval）的下限、上限，某个回归系数的置信区间以 95%的置信度包含该回归系数 。注意并不是指样本数据落在这一区间的概率为 95%。

此外，还有一些重要的指标需要关注：

R-squared：R方判定系数（Coefficient of determination），表示所有自变量对因变量的联合的影响程度，用于度量回归方程拟合度的好坏，越接近于 1说明拟合程度越好。

F-statistic：F 统计量（F-Statistic），用于对整体回归方程进行显著性检验，检验所有自变量在整体上对因变量的影响是否显著。

Statsmodels 也可以通过属性获取所需的回归分析的数据，例如：

print(“OLS model: Y = b0 + b1 * x”) # b0: 回归直线的截距，b1: 回归直线的斜率
print('Parameters: ', results.params) # 输出：拟合模型的系数
yFit = results.fittedvalues # 拟合模型计算出的 y值
ax.plot(x1, yTest, ‘o', label=“data”) # 原始数据
ax.plot(x1, yFit, ‘r-', label=“OLS”) # 拟合数据

3、一元线性回归

3.1 一元线性回归 Python 程序：

# LinearRegression_v1.py
# Linear Regression with statsmodels (OLS: Ordinary Least Squares)
# v1.0: 调用 statsmodels 实现一元线性回归
# 日期：2021-05-04
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.sandbox.regression.predstd import wls_prediction_std
def main():  # 主程序
    # 生成测试数据:
    nSample = 100
    x1 = np.linspace(0, 10, nSample)  # 起点为 0，终点为 10，均分为 nSample个点
    e = np.random.normal(size=len(x1))  # 正态分布随机数
    yTrue = 2.36 + 1.58 * x1  #  y = b0 + b1*x1
    yTest = yTrue + e  # 产生模型数据
    # 一元线性回归：最小二乘法(OLS)
    X = sm.add_constant(x1)  # 向矩阵 X 添加截距列（x0=[1,...1]）
    model = sm.OLS(yTest, X)  # 建立最小二乘模型（OLS）
    results = model.fit()  # 返回模型拟合结果
    yFit = results.fittedvalues  # 模型拟合的 y值
    prstd, ivLow, ivUp = wls_prediction_std(results) # 返回标准偏差和置信区间
    # OLS model: Y = b0 + b1*X + e
    print(results.summary())  # 输出回归分析的摘要
    print("\nOLS model: Y = b0 + b1 * x")  # b0: 回归直线的截距，b1: 回归直线的斜率
    print('Parameters: ', results.params)  # 输出：拟合模型的系数
    # 绘图：原始数据点，拟合曲线，置信区间
    fig, ax = plt.subplots(figsize=(10, 8))
    ax.plot(x1, yTest, 'o', label="data")  # 原始数据
    ax.plot(x1, yFit, 'r-', label="OLS")  # 拟合数据
    ax.plot(x1, ivUp, '--',color='orange',label="upConf")  # 95% 置信区间 上限
    ax.plot(x1, ivLow, '--',color='orange',label="lowConf")  # 95% 置信区间 下限
    ax.legend(loc='best')  # 显示图例
    plt.title('OLS linear regression ')
    plt.show()
    return
if __name__ == '__main__': #YouCans, XUPT
    main()

3.2 一元线性回归 程序运行结果：

OLS Regression Results
==============================================================================
Dep. Variable:                      y   R-squared:                       0.961
Model:                            OLS   Adj. R-squared:                  0.961
Method:                 Least Squares   F-statistic:                     2431.
Date:                Wed, 05 May 2021   Prob (F-statistic):           5.50e-71
Time:                        16:24:22   Log-Likelihood:                -134.62
No. Observations:                 100   AIC:                             273.2
Df Residuals:                      98   BIC:                             278.5
Df Model:                           1
Covariance Type:            nonrobust
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const          2.4669      0.186     13.230      0.000       2.097       2.837
x1             1.5883      0.032     49.304      0.000       1.524       1.652
==============================================================================
Omnibus:                        0.070   Durbin-Watson:                   2.016
Prob(Omnibus):                  0.966   Jarque-Bera (JB):                0.187
Skew:                           0.056   Prob(JB):                        0.911
Kurtosis:                       2.820   Cond. No.                         11.7
==============================================================================
OLS model: Y = b0 + b1 * x
Parameters:  [2.46688389 1.58832741]

4、多元线性回归

4.1 多元线性回归 Python 程序：

# LinearRegression_v2.py
# Linear Regression with statsmodels (OLS: Ordinary Least Squares)
# v2.0: 调用 statsmodels 实现多元线性回归
# 日期：2021-05-04
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.sandbox.regression.predstd import wls_prediction_std
# 主程序
def main():  # 主程序
    # 生成测试数据:
    nSample = 100
    x0 = np.ones(nSample)  # 截距列 x0=[1,...1]
    x1 = np.linspace(0, 20, nSample)  # 起点为 0，终点为 10，均分为 nSample个点
    x2 = np.sin(x1)
    x3 = (x1-5)**2
    X = np.column_stack((x0, x1, x2, x3))  # (nSample,4): [x0,x1,x2,...,xm]
    beta = [5., 0.5, 0.5, -0.02] # beta = [b1,b2,...,bm]
    yTrue = np.dot(X, beta)  # 向量点积 y = b1*x1 + ...+ bm*xm
    yTest = yTrue + 0.5 * np.random.normal(size=nSample)  # 产生模型数据
    # 多元线性回归：最小二乘法(OLS)
    model = sm.OLS(yTest, X)  # 建立 OLS 模型: Y = b0 + b1*X + ... + bm*Xm + e
    results = model.fit()  # 返回模型拟合结果
    yFit = results.fittedvalues  # 模型拟合的 y值
    print(results.summary())  # 输出回归分析的摘要
    print("\nOLS model: Y = b0 + b1*X + ... + bm*Xm")
    print('Parameters: ', results.params)  # 输出：拟合模型的系数
    # 绘图：原始数据点，拟合曲线，置信区间
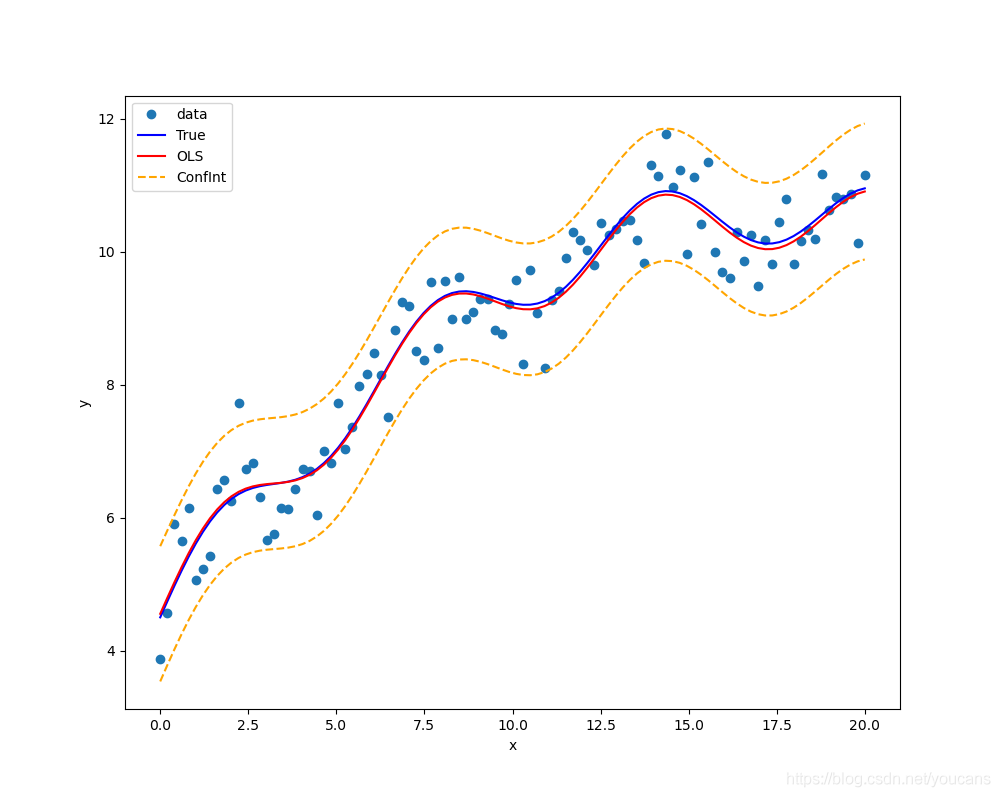
    prstd, ivLow, ivUp = wls_prediction_std(results) # 返回标准偏差和置信区间
    fig, ax = plt.subplots(figsize=(10, 8))
    ax.plot(x1, yTest, 'o', label="data")  # 实验数据（原始数据+误差）
    ax.plot(x1, yTrue, 'b-', label="True")  # 原始数据
    ax.plot(x1, yFit, 'r-', label="OLS")  # 拟合数据
    ax.plot(x1, ivUp, '--',color='orange', label="ConfInt")  # 置信区间 上届
    ax.plot(x1, ivLow, '--',color='orange')  # 置信区间 下届
    ax.legend(loc='best')  # 显示图例
    plt.xlabel('x')
    plt.ylabel('y')
    plt.show()
    return
if __name__ == '__main__':
    main()

4.2 多元线性回归 程序运行结果：

OLS Regression Results
==============================================================================
Dep. Variable:                      y   R-squared:                       0.932
Model:                            OLS   Adj. R-squared:                  0.930
Method:                 Least Squares   F-statistic:                     440.0
Date:                Thu, 06 May 2021   Prob (F-statistic):           6.04e-56
Time:                        10:38:51   Log-Likelihood:                -68.709
No. Observations:                 100   AIC:                             145.4
Df Residuals:                      96   BIC:                             155.8
Df Model:                           3
Covariance Type:            nonrobust
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const          5.0411      0.120     41.866      0.000       4.802       5.280
x1             0.4894      0.019     26.351      0.000       0.452       0.526
x2             0.5158      0.072      7.187      0.000       0.373       0.658
x3            -0.0195      0.002    -11.957      0.000      -0.023      -0.016
==============================================================================
Omnibus:                        1.472   Durbin-Watson:                   1.824
Prob(Omnibus):                  0.479   Jarque-Bera (JB):                1.194
Skew:                           0.011   Prob(JB):                        0.551
Kurtosis:                       2.465   Cond. No.                         223.
==============================================================================
OLS model: Y = b0 + b1*X + ... + bm*Xm
Parameters:  [ 5.04111867  0.4893574   0.51579806 -0.01951219]

5、附录：回归结果详细说明

Dep.Variable: y 因变量
    Model：OLS 最小二乘模型
    Method: Least Squares 最小二乘
    No. Observations: 样本数据的数量
    Df Residuals：残差自由度(degree of freedom of residuals)
    Df Model：模型自由度(degree of freedom of model)
    Covariance Type：nonrobust 协方差阵的稳健性
    R-squared：R 判定系数
    Adj. R-squared: 修正的判定系数
    F-statistic： 统计检验 F 统计量
    Prob (F-statistic): F检验的 P值
    Log likelihood: 对数似然    coef：自变量和常数项的系数，b1,b2,...bm,b0
    std err：系数估计的标准误差
    t：统计检验 t 统计量
    P>|t|：t 检验的 P值
    [0.025, 0.975]：估计参数的 95%置信区间的下限和上限
    Omnibus：基于峰度和偏度进行数据正态性的检验
    Prob(Omnibus)：基于峰度和偏度进行数据正态性的检验概率
    Durbin-Watson：检验残差中是否存在自相关
    Skewness：偏度，反映数据分布的非对称程度
    Kurtosis：峰度，反映数据分布陡峭或平滑程度
    Jarque-Bera(JB)：基于峰度和偏度对数据正态性的检验
    Prob(JB)：Jarque-Bera(JB)检验的 P值。
    Cond. No.：检验变量之间是否存在精确相关关系或高度相关关系。

以上就是Python数学建模StatsModels统计回归之线性回归示例详解的详细内容，更多关于数学建模StatsModels统计回归之线性回归的资料请关注我们其它相关文章！